Princípios de conservação e Equação de Evolução

Os princípios fundamentais da Mecânica aplicam-se a corpos materiais e por isso

em fluidos aplicam-se a uma porção de fluido e não a um volume fixo do espaço.

Este texto descreve os princípios de Conservação da massa e a lei de Newton e

mostra como, usando o chamado teorema de Reynolds, se passa de um volume

material para um volume do espaço. Implicitamente o texto mostra o significado de

derivada total (ou material), de derivada local temporal e de derivada convectiva. O

texto termina apresentando a forma geral de uma equação de evolução.

1.1 CONSERVAÇÃO DA MASSA:

A lei de conservação da massa foi “popularizada” pela frase do químico francês

Lavoisier “Nada se ganha, nada se perde, tudo se transforma”. Efectivamente, o que

esta frase pretende dizer é que a massa se conserva:

0=dtdM

Esta equação só é posta em causa pela teoria da relatividade, onde a massa se

pode transformar em energia.

1.2 LEI DE NEWTON, QUANTIDADE DE MOVIMENTO E ENERGIA

CINÉTICA

A lei de Newton diz que a resultante das forças aplicadas a um corpo é igual ao

produto da massa pela aceleração:

dtdvMF

dtvdMF i

i⇔=rr

utilizando a lei da conservação da massa, a lei de Newton pode ser escrita como

uma equação de evolução da quantidade de movimento, em vez de ser uma

equação de evolução da velocidade.

( )dtvMd

dtdMv

dtvdMF

rrr=+=

Esta equação diz que a resultante das forças aplicadas a um corpo é igual à taxa de

variação da sua quantidade de movimento. A lei de Newton permite também analisar

melhor o significado de quantidade de movimento. Integrando a força e a aceleração

do corpo ao longo do tempo obtém-se:

vMvMddtdtvdMdtF

dtvdMF

V

v

TTrr

rrrr==

==>= ∫∫∫

=000

Esta equação mostra que a quantidade de movimento de um corpo é o integral

temporal do somatório das forças aplicadas ao corpo. Isso mostra que forças

pequenas podem ser determinantes para um escoamento se actuarem ao longo de

muito tempo. É o que se passa na atmosfera e no oceano com a força de coriolis.

Perceber a diferença entre quantidade de movimento e energia cinética é um

aspecto crítico para a mecânica dos fluidos. Energia = Trabalho. Então:

( ) ( )2122

2

1

2

1

2

1

2

121 VVvdvMdtv

dtvdMed

dtvdMedF

v

v

e

e

e

e

e

e

−==

=

= ∫∫∫∫

rrrr

rr

rr

Esta equação mostra que o trabalho das forças que actuam um corpo é igual à

variação da sua energia cinética durante esse período. Enquanto que a quantidade

de movimento varia desde que a resultante das forças aplicadas sobre o corpo seja

não nula, a energia cinética só varia se existir trabalho. Assim, as forças

perpendiculares ao movimento modificam a quantidade de movimento, mas não lhe

modificam a energia cinética.

1.3 TEOREMA DE REYNOLDS

A lei de conservação da massa e a lei de Newton aplicam-se a um volume material -

frequentemente designado por “sistema”. O teorema de Reynolds permite relacionar

um volume material “sistema” e um volume fixo do espaço. Consideremos o conjunto

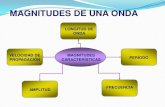
dos 3 volumes materiais e volume de controlo representados na Figura 1. O volume

de controlo fixo é coincidente com o sistema material 2, no instante inicial (t0). Seja B

o valor de uma propriedade genérica. Seja:

Bsistema I : valor total da propriedade no sistema i (com i =1, 2 ou 3)

Bvc: valor total da propriedade no volume de controlo.

Figura 1: Conjunto de três volumes materiais e de um volume de controlo fixo no espaço. O

volume material “2” coincide com o volume de controlo no instante “t0”.

A taxa de Variação da propriedade no Sistema i será:

( ) ( )t

BB 00 tsistemaI

ttsistemaI

∆−∆+

e no volume de controlo será:

( ) ( )t

BB 00 tvc

ttvc

∆−∆+

No instante t0 o sistema 2 coincidia com o volume de controlo e portanto:

( ) ( ) 00 t2sistema

tvc BB =

em t0 + ∆t a relação entre ambos é dada pelo que entra, menos o que sai:

( ) ( ) sai_que_massaentra_que_massaBB tt2sistema

ttvc

00 −+= ∆+∆+

Vol. de

controlo

Sistema 3 Sistema 2 Sistema 1

Três porções de fluido

(sistemas 1, 2 e 3) no instante

inicial T0.

então a taxa de variação no volume de controlo pode ser relacionada com a taxa de

variação no sistema que o ocupava no início do intervalo de tempo substituindo as

expressões anteriores na que dá a taxa de variação no volume de controlo:

( ) ( )t

BB 00 tvc

ttvc

∆−∆+

=

( ) ( )( )t

sai_que_quantidadeentra_que_quantidadet

BB 00 t2sistema

tt2sistema

∆−

+∆−∆+

As quantidades que entram ou saem por unidade de tempo designam-se por fluxos

A quantidade total da propriedade existente no interior do volume é dada pelo

integral no volume do valor específico dessa propriedade (β =dBdV

)

∫∫∫= dVB β

Os fluxos podem ser advectivos ou difusivos. O fluxo advectivo representa o

transporte pela velocidade, sendo dado por:

( )dAnvadvB ∫∫=Φrr.β

A velocidade é medida sobre a superfície e por conseguinte é a velocidade relativa.

à superfície do volume. No caso do volume de controlo fixo é a velocidade do

escoamento e no caso do volume material é “zero” pois este desloca-se à

velocidade do escoamento.

O fluxo difusivo pode ser calculado a partir da lei de Fick:

( ) dAndAnx

dif jj

B ∫∫∫∫ ∇−=

−=Φ

rr.. βκ

∂∂βκ

Este fluxo existe desde que existam gradientes da propriedade. Por conseguinte o

fluxo existe através das faces do volume fixo e do volume material, sendo o mesmo

quando eles são coincidentes. Deste modo este fluxo não contribui para as

diferenças entre o que se passa no interior de cada um dos volumes de controlo (fixo

e material) e não deve ser considerado na equação que relaciona ambos os

volumes.

O que se passa no interior de ambos os volumes pode então ser relacionado pela

equação:

( )dAn.vdVdtddV

t surfacesistemavc∫∫∫∫∫∫∫∫ −=

rrβββ

∂∂

Se o volume for suficientemente pequeno (volume elementar, ∆V) para que β possa

ser considerado constante no seu interior e nas suas faces, bem como a velocidade

e a difusividade, esta equação pode ser escrita como:

( ) ( ) saidaentrada AnvAnvVdtdV

t∆−∆−∆=∆

rrrr.. ββββ

∂∂

Mas

k

k

xuV

dt)(dV

dt)V(d

dt)(dV

dt)V(d

∂∂∆ββ∆∆ββ∆∆β

+=+=

Se o volume de controlo for indeformável e tiver as faces alinhadas com os eixos

coordenados, com comprimentos ∆xj a equação escreve-se como:

( ) ( )

( ) ( ) ( ) ( )3312

11

321332122312231

132113221 3

xxxxx

xxx

vxxvxxvxxvxx

vxxvxxtVd

txxx

∆+∆+

∆+

∆∆−∆∆+∆∆−∆∆

+∆∆−∆∆+

∆∆

=∆∆∆

ββββ

βββ∂∂β

substituindo a equação anterior nesta e fazendo tender ∆xj para zero, obtém-se:

( )jjk

k vxx

vdtd

tβ

∂∂

∂∂ββ

∂∂β

−+= , ou k

k

j

j

xv

xv

tdtd

∂∂β

∂∂β

∂∂ββ

−+=

Desenvolvendo o segundo termo do segundo membro obtém-se a expressão da

derivada total temporal em função da derivada local temporal e da derivada

convectiva:

jj x

vtdt

d∂∂β

∂∂ββ

+=

A derivada total representa por conseguinte a taxa de variação de uma propriedade

no interior de um volume material, enquanto que a derivada local representa a taxa

de variação num volume fixo (derivada local temporal) e a derivada convectiva

representa a divergência do fluxo advectivo e por conseguinte o transporte pelo

campo de velocidades.

2 Equação de Transporte

No parágrafo anterior quantificámos:

• O valor total de uma propriedade no interior de um volume de controlo

(integral do valor específico dessa propriedade no interior do volume de

controlo);

• Escrevemos a taxa de variação temporal dessa propriedade num volume de

controlo fixo e numa porção de fluido (sistema);

• Verificámos que a variação no seio de um volume de controlo fixo e no seio

do fluido que está a passar por esse volume de controlo fixo estão

relacionadas pelo integral do fluxo advectivo ao longo da superfície do

volume fixo e que por isso a taxa de variação no interior de volume fixo pode

ser sintetizada como “a taxa de variação de uma propriedade no interior de

um volume de controlo é igual ao que entra, menos o que sai, mais a taxa de

variação no seio de fluido em movimento”

• Fazendo tender o volume de controlo para zero, verificámos que a relação

entre a taxa de variação no seio do fluido e num volume fixo é dada pela

relação entre as derivadas total e parcial temporal, representando a derivada

convectiva o integral do fluxo convectivo ao longo da superfície do volume de

controlo.

Aquando da introdução do conceito do fluido como meio continuo e do conceito de

velocidade num escoamento foi mostrado que o movimento browniano das

moléculas não é quantificado pela velocidade. O efeito desse movimento resulta

num transporte à escala molecular cuja intensidade está associada à facilidade do

movimento das moléculas, quantificada através da difusividade. O fluxo resultante

deste movimento depende da difusividade e do gradiente da propriedade, de acordo

com a lei de Fick (também chamada de Fourier, quando se trata de calor).

No caso de a propriedade transportada ser a quantidade de movimento e de se

tratar de líquidos, os processos de escala molecular envolvem o rompimento de

grupos de moléculas. Por esta razão a difusividade de quantidade de movimento é

tratada de forma diferente da difusividade de outras propriedades, sendo designada

por viscosidade.

Depois dos conceitos introduzidos acima, estamos agora em condições de escrever

a equação de evolução (ou de transporte) de uma propriedade. No seio de um fluido

em movimento uma propriedade pode evoluir devido aos processos de produção e

destruição (frequentemente designados por “fontes e poços”) ou devido ao fluxo

difusivo através da sua superfície, não quantificado através da velocidade do fluido.

O transporte pela velocidade permitirá relacionar a equação para um volume de

fluido em movimento, com a equação para outro volume de fluido.

Consideremos de novo os volumes de controlo fixo e material, coincidentes no

instante t0. Calculando os fluxos vamos relacionar o valor de uma propriedade no

instante t0, no interior do volume de controlo fixo com o seu valor num instante t0+∆t.

A partir do conceito de derivada total passaremos da equação no volume fixo para a

equação para um volume material.

Para calcular a taxa de variação no interior do volume teremos que considerar os

fluxos difusivo e advectivo:

( )( )dAn.kn.vdVt surfacevc

∫∫∫∫∫ ∇−−=rrrr

βββ∂∂

Definindo um volume de controlo paralelepipédico, indeformável, os fluxos podem

ser expressos em termos das 3 componentes da velocidade e dos gradientes:

∆ ∆ ∆∆∆

∆ ∆ ∆ ∆

∆ ∆ ∆ ∆ ∆ ∆ ∆ ∆

∆

∆

x x xt

d Vt

x x vx

x x vx

x x vx

x x vx

x x vx

x

x x x

x x x

1 2 2 3 11 1

2 3 11

1 3 22 2

1 3 22 2

1 2 33

1

3

3

1 1

2 1

∂β∂

ββ κ

∂ββ κ

∂β

β κ∂β

β κ∂β

β κ∂β

=

+ −

− −

+

−

− −

+ −

−

+

+

x vx

x x2 3

33 3

β κ∂β

−

+∆

Fazendo de novo tender o volume para zero obtém-se a equação de transporte em

coordenadas cartesianas:

−−=

xjv

xxv

t jjk

k ∂βκβ∂∂

∂∂β

∂∂β

ou desenvolvendo o termo convectivo:

+−−=

xjxxv

xv

xv

t jjj

j

j

k

k ∂βκ∂∂

∂∂β

∂∂

β∂∂β

∂∂β

O primeiro e segundo termos do segundo membro da equação anulam-se.

Considerando a relação entre a derivada local temporal e a derivada total a equação

pode ser escrita como:

=+=

xjxxv

tdtd

jjj

∂βκ∂∂

∂∂β

∂∂ββ

No caso de a propriedade β ter fontes ou poços (não ser conservativa) a equação

deverá ser escrita como:

( )PFxjxx

vtdt

d

jjj −+

=+=

∂βκ∂∂

∂∂β

∂∂ββ

Quando consideramos um volume de controlo que acompanha o fluido estamos a

usar um formalismo lagrangeano (derivada total = difusão + fontes – poços),

enquanto que quando consideramos um ponto fixo do espaço estamos a usar um

formalismo euleriano (derivada local=advecção+difusão+fontes - poços).

Se a propriedade transportada for a massa volúmica do fluido, o termo difusivo é

nulo e a produção/destruição dependem da divergência da velocidade. Fazendo β=ρ

e j

jx

vPF ∂∂

−=− ρ)(

Obtém-se a equação da continuidade. Fazendo β=ρvi e (F-P) = Somatório das forças

aplicadas, obtém-se a equação de transporte de quantidade de movimento.

3 Nota final

Este texto apresenta o conceito de equação de evolução para uma propriedade

genérica como”o somatório do que entra mais o que sai, mais o que se produz e

menos o que se destrói”. O texto mostra ainda a relação entre um volume material

(formulação lagrangeana) e um volume de controlo fixo (formulação eulerianas),

mostrando que ambas estão relacionadas pelo fluxo advectivo, da mesma maneira

que a derivada total temporal (lagrangeana) está relacionada com a parcial pela

derivada convectiva, a qual, em termos diferenciais tem o mesmo significado que o

integral do fluxo advectivo numa formulação integral.

Estas equações são a base do estudos dos processos de transporte de qualquer

propriedade no ambiente e da própria mecânica dos fluidos. As equações mostram

que quando as equações se tornam não lineares quando a propriedade transportada

é a velocidade. Essa não linearidade advém do facto de a velocidade se transportar

a ela própria e é responsável pelo facto de as chamadas forças de inércia (massa

vezes aceleração) serem proporcionais ao quadrado da velocidade.