CONTROLE DE SISTEMAS INCERTOS COM ATRASO USANDO …

CONTROLE DE SISTEMAS INCERTOS COM ATRASO

USANDO TECNICAS BASEADAS EM CONTROLE POR

MODOS DESLIZANTES INTEGRAL E LMI

Pedro Vicente Santos

Projeto de Graduacao apresentado ao Curso

de Engenharia Eletronica e de Computacao

da Escola Politecnica, Universidade Federal

do Rio de Janeiro, como parte dos requisitos

necessarios a obtencao do tıtulo de Enge-

nheiro.

Orientador: Eduardo Vieira Leao Nunes

Rio de Janeiro

Agosto de 2018

UNIVERSIDADE FEDERAL DO RIO DE JANEIRO

Escola Politecnica - Departamento de Eletronica e de Computacao

Centro de Tecnologia, bloco H, sala H-217, Cidade Universitaria

Rio de Janeiro - RJ CEP 21949-900

Este exemplar e de propriedade da Universidade Federal do Rio de Janeiro, que

podera incluı-lo em base de dados, armazenar em computador, microfilmar ou adotar

qualquer forma de arquivamento.

E permitida a mencao, reproducao parcial ou integral e a transmissao entre bibli-

otecas deste trabalho, sem modificacao de seu texto, em qualquer meio que esteja

ou venha a ser fixado, para pesquisa academica, comentarios e citacoes, desde que

sem finalidade comercial e que seja feita a referencia bibliografica completa.

Os conceitos expressos neste trabalho sao de responsabilidade do(s) autor(es).

iv

DEDICATORIA

A minha mae, Valeria, cujo apoio foi fundamental para que eu completasse esta

etapa da minha vida.

v

AGRADECIMENTO

Agradeco a minha mae e amigos, pelo incentivo e pela forca que me deram para

superar as dificuldades. Tambem agradeco ao Professor Eduardo Vieira Leao Nunes

pela orientacao e ajuda na elaboracao deste trabalho. Por fim, agradeco ao Conselho

Nacional de Desenvolvimento Cientıfico e Tecnologico (CNPq) pela oportunidade de

participar em atividades na area de pesquisa.

vi

RESUMO

Este trabalho apresenta algumas das principais caracterısticas de sistemas com

atraso, assim como os motivos que fazem com que o controle por modos deslizantes

possa ser tao vantajoso para lidar com modelagem incerta. Inicialmente, um breve

estudo sobre as principais caracterısticas e propriedades do controle por modos des-

lizantes e apresentado, incluindo o controle por modos deslizantes integral. Essa

tecnica procura garantir que o sistema seja robusto a incertezas e perturbacoes du-

rante todo o tempo ao assegurar que o sistema sempre se encontre em deslizamento.

Neste projeto e proposta uma modificacao para uma tecnica baseada em controle

por modos deslizantes integral para sistemas com atraso na entrada e tambem no es-

tado. A analise de estabilidade do esquema de controle e baseada em Desigualdades

Matriciais Lineares (Linear Matrix Inequalities - LMI). Por meio dessa ferramenta e

possıvel obter condicoes suficientes para assegurar a estabilidade global do sistema

em malha fechada. Para a solucao de LMI tres pacotes computacionais sao conside-

rados e brevemente discutidos. Alem disso, um pequeno tutorial sobre esses pacotes

e elaborado.

Palavras-Chave: Controle por Modos Deslizantes Integral, LMI, Sistemas com

Atraso.

vii

ABSTRACT

This work presents some of the main characteristics of time delay systems, as

well as the reasons why Sliding Mode Control can be so advantageous to deal with

uncertain modeling. Initially, a brief study of main characteristics and properties of

Sliding Mode Control is presented, including Integral Sliding Mode Control. This

technique seeks to ensure that the system is robust to uncertainties and disturban-

ces at all times by ensuring that the system is always in the sliding surface. In this

project a modification is proposed for a technique based on Integral Sliding Mode

Control for systems with input and state delays. The stability analysis of the con-

trol scheme is based on Linear Matrix Inequalities (LMI). Through this tool it is

possible to obtain sufficient conditions to ensure the overall stability of the closed

loop system. For the LMI solution three computational packages are considered and

briefly discussed. In addition, a small tutorial on these packages is developed.

Key-words: Integral Sliding Mode Control, LMI, time delay systems.

viii

SIGLAS

FDEs - Functional Differential Equations

ISMC - Integral Sliding Mode Control

LMI - Linear Matrix Inequalities

LTI - Linear Time-Invariant

NDEs - Neutral Type Differential Equations

ODEs - Ordinary Differential Equations

RDEs - Retarded Differential Equations

SPD - Semidefinite Programming

SMC - Sliding Mode Control

TDS - Time Delay System

ix

Sumario

1 Introducao 1

1.1 Tema . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

1.2 Delimitacao . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

1.3 Justificativa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

1.4 Objetivos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

1.5 Metodologia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

1.6 Descricao . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

2 Conceitos Matematicos 5

2.1 Matrizes positivas definidas . . . . . . . . . . . . . . . . . . . . . . . 5

2.2 Complemento de Schur . . . . . . . . . . . . . . . . . . . . . . . . . . 8

2.3 Teoria de Lyapunov . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

3 Controle por Modos Deslizantes 17

3.1 Sistema de Controle Descontınuo . . . . . . . . . . . . . . . . . . . . 18

3.2 Nocoes Basicas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

3.3 Existencia dos Modos Deslizantes . . . . . . . . . . . . . . . . . . . . 24

3.4 Metodo da Regularizacao . . . . . . . . . . . . . . . . . . . . . . . . . 27

3.5 Metodo do Controle Equivalente . . . . . . . . . . . . . . . . . . . . . 29

3.6 Controle por Modos Deslizantes Integral . . . . . . . . . . . . . . . . 31

3.6.1 Definicao do Problema . . . . . . . . . . . . . . . . . . . . . . 32

3.6.2 Princıpios do Projeto . . . . . . . . . . . . . . . . . . . . . . . 33

3.6.3 Superfıcie de Deslizamento Integral . . . . . . . . . . . . . . . 35

3.6.4 Leis de controle . . . . . . . . . . . . . . . . . . . . . . . . . . 36

3.6.5 Condicao de Alcancabilidade . . . . . . . . . . . . . . . . . . . 37

x

3.6.6 Propriedades . . . . . . . . . . . . . . . . . . . . . . . . . . . 38

3.7 Chattering . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38

4 Sistemas com atraso 41

4.1 Introducao . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41

4.2 Conceito de solucao . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44

4.3 Tipos de atrasos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49

4.3.1 Atrasos Constantes . . . . . . . . . . . . . . . . . . . . . . . . 50

4.3.2 Atrasos variantes no tempo . . . . . . . . . . . . . . . . . . . 50

4.4 Tipos de TDSs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52

5 Estabilidade e Desigualdades Matriciais Lineares 55

5.1 LMIs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55

5.2 Estabilidade de TDSs . . . . . . . . . . . . . . . . . . . . . . . . . . . 60

5.3 Lyapunov-Krasovskii . . . . . . . . . . . . . . . . . . . . . . . . . . . 62

5.3.1 Condicoes para estabilidade de TDSs . . . . . . . . . . . . . . 62

6 SMC aplicado a Sistemas com Atraso 65

6.1 Formulacao do Problema . . . . . . . . . . . . . . . . . . . . . . . . . 66

6.2 Projeto da superfıcie de deslizamento . . . . . . . . . . . . . . . . . . 67

6.3 Projeto do controlador . . . . . . . . . . . . . . . . . . . . . . . . . . 69

6.4 Exemplo Ilustrativo . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72

7 Conclusao 76

Bibliografia 78

A Toolboxs para resolucao de LMIs 82

A.1 LMI Control Toolbox . . . . . . . . . . . . . . . . . . . . . . . . . . . 83

A.2 Yalmip . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86

A.3 CVX . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89

A.4 Comparacao entre os Toolboxs . . . . . . . . . . . . . . . . . . . . . . 90

xi

Lista de Figuras

2.1 Conceitos de estabilidade. . . . . . . . . . . . . . . . . . . . . . . . . . 13

3.1 Plano de fase para o sistema (3.2). . . . . . . . . . . . . . . . . . . . . . 20



3.4 Grafico de x x t para o sistema (3.1). . . . . . . . . . . . . . . . . . . . 21

3.5 Exemplos de trajetorias proximas da superfıcie de deslizamento e sinais de

controle para um sistema com histerese. . . . . . . . . . . . . . . . . . . 23


3.7 Ilustracao do deslizamento local. . . . . . . . . . . . . . . . . . . . . . . 27

3.8 Plano de fase para o sistema (3.13). . . . . . . . . . . . . . . . . . . . . 30

3.9 (a) Grafico de x x t para o sistema (3.13); (b) Grafico de x x t para o

sistema (3.15); (c) Sinal de controle para o sistema (3.13); (d) Sinal de

controle para o sistema (3.15). . . . . . . . . . . . . . . . . . . . . . . . 31

3.10 Sinal de controle: (a) Rele; (b) Saturacao para σ = 1. . . . . . . . . . . . 40

4.1 Esquematico de um sistema simples com atraso. . . . . . . . . . . . . . . 42

4.2 Diagrama de Bode para o termo de atraso puro. . . . . . . . . . . . . . . 43

4.3 Resposta ao degrau do sistema (4.3) considerando a possibilidade de um

ganho proporcional. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44

4.4 Solucao do sistema (4.1). . . . . . . . . . . . . . . . . . . . . . . . . . . 46

4.5 Solucao do sistema (4.8). . . . . . . . . . . . . . . . . . . . . . . . . . . 48

6.1 Trajetorias do sistema do exemplo considerado. . . . . . . . . . . . . . . 74

6.2 Sinal de controle do exemplo considerado. . . . . . . . . . . . . . . . . . 74

6.3 Superfıcie de deslizamento do exemplo considerado. . . . . . . . . . . . . 74

6.4 Superfıcie de deslizamento projetada como em [4]. . . . . . . . . . . . . . 75

xii

Capıtulo 1

Introducao

1.1 Tema

Este trabalho tem como tema o controle de sistemas com atraso e com modelo

dinamico incerto. Dentro desse contexto, sao abordadas tecnicas de controle basea-

das no controle por modos deslizantes (Sliding Mode Control - SMC ) e sao utilizados

a teoria de Lyapunov e o conceito de desigualdades matriciais lineares (Linear Matrix

Inequalities - LMI ) para analisar a estabilidade do sistema.

1.2 Delimitacao

O objeto de estudo sao as tecnicas de controle baseadas no SMC, mais especifica-

mente no controle por modos deslizantes integral (Integral Sliding Mode Control -

ISMC ). Tais tecnicas foram escolhidas por serem eficientes para lidar com sistemas

incertos. Alem disso, o estudo foi restrito a sistemas lineares que possuem atraso,

que pode ser constante ou variavel, na entrada e/ou na sua dinamica. Com relacao a

descricao matematica dos sistemas considerados, o estudo foi restrito a equacoes di-

ferenciais retardadas (Retarded Differential Equations - RDEs) e ao caso de sistemas

com atraso discreto.

1

1.3 Justificativa

Para sistemas dinamicos de dimensao finita, as condicoes iniciais dependem apenas

de um conjunto finito de valores, mais especificamente os valores das variaveis de

estado nesse instante de tempo inicial. Ja no caso de sistemas com atraso e preciso ter

mais informacoes. Para cada instante de tempo, nao basta apenas o conhecimento

do valor de certas variaveis para um dado instante de tempo, e preciso saber o

comportamento previo dessas variaveis em uma janela tempo. Dessa forma, sistemas

com atraso sao sistemas de dimensao infinita e o seu estado consiste de um conjunto

infinito de valores. Esse aspecto torna a analise desse tipo de sistema ainda mais

desafiadora.

Sistemas de controle com atrasos sao muito comuns, dado que normalmente existe

um tempo para adquirir a informacao necessaria para a tomada de decisoes e para

a execucao das mesmas. E valido tambem ressaltar que estudos comprovam que a

introducao cuidadosa de atrasos podem estabilizar um sistema que antes era instavel.

Um exemplo conhecido que possui esse comportamento e o seguinte sistema:

y(t) + y(t)− y(t− h) = 0

O sistema acima e instavel para h = 0, mas e assintoticamente estavel para h = 1

[1]. Esse paradoxo e um dos motivos para os anos de interesse no estudo de sistemas

com atraso [2, 1].

Alem disso, sistemas dinamicos muitas vezes sao caracterizados por serem incer-

tos, o que significa que possuem modelagem precaria ou grandes incertezas e per-

turbacoes. Essas perturbacoes podem ocorrer devido a dinamicas nao modeladas,

variacoes nos parametros da planta e por disturbios externos [3].

Caso esses atrasos e/ou incertezas sejam desconsiderados, o modelo criado para o

sistema pode nao funcionar perfeitamente e levar a uma performance insatisfatoria

[3, 4, 5]. Neste sentido, existe uma motivacao para o estudo de tecnicas de controle

baseadas em modos deslizantes, devido a sua eficiencia no controle de sistemas in-

certos, principalmente por sua robustez com respeito a estabilidade e desempenho

2

[6, 5, 7].

1.4 Objetivos

O principal objetivo desse trabalho e estudar e desenvolver tecnicas de controle

por modos deslizantes para sistemas incertos com atraso. Para alcancar essa meta os

seguintes objetivos especıficos devem ser atingidos: estudo das principais proprieda-

des de sistemas com atraso e do controle por modos deslizantes, revisao da literatura

para encontrar tecnicas modernas para o controle desse tipo de sistema, analise e

desenvolvimento do algoritmo de controle e validacao da estrategia escolhida por

meio de simulacoes numericas.

1.5 Metodologia

Primeiramente, foi realizado um estudo com enfase no controle por modos des-

lizantes e suas principais propriedades foram verificadas por meio de simulacoes

numericas. O SMC e conhecido pelas seguintes vantagens: estabilidade, rejeicao de

pertubacoes e robustez [3]. Alem disso, com este tipo de controle e possıvel combi-

nar caracterısticas uteis de cada estrutura do sistema realimentado, ou ate mesmo se

obter propriedades que nao estao presentes em nenhumas das estruturas utilizadas

[8, 9, 10, 11]. Dentro do SMC, foi estudado de forma mais aprofundada o controle

por modos deslizantes integral (ISMC) devido a sua capacidade de garantir que a

robustez do controlador seja valida por todo o tempo de resposta do sistema. Alem

disso, com o ISMC e possıvel lidar de forma mais adequada com incertezas desca-

sadas, o que nao acontece no SMC convencional. Por esses motivos, o ISMC sera

utilizado para lidar com o tipo de sistema encontrado neste trabalho.

Em seguida foi feito o estudo das principais caracterısticas de sistemas com atraso.

Um problema encontrado e que sistemas deste tipo costumam funcionar melhor com

ganhos baixos, enquanto o SMC e baseado em alto ganho. Logo, esse trabalho tera

que lidar com essa dificuldade para obter um sistema com bom desempenho.

3

Durante o desenvolvimento do controle do sistema, e necessario garantir que o

mesmo seja estavel assintoticamente em malha fechada. Esse trabalho faz uso das

LMIs para analise da estabilidade do sistema. As LMIs tem ganhado cada vez mais

forca atualmente, pois com elas e possıvel modelar uma variedade de problemas da

teoria de controle, alem de representarem problemas de otimizacao convexos, que

sao de facil solucao numerica usando os softwares atuais [12].

Dessa forma, neste trabalho a analise da estabilidade parte de uma funcao de Lya-

punov, obtendo uma condicao suficiente para a estabilidade assintotica do sistema

por meio de LMIs [13, 4].

1.6 Descricao

No capıtulo 2 sao abordadas alguns conceitos matematicos importantes que estao

presentes ao longo do texto.

O capıtulo 3 faz uso de simulacoes numericas e apresenta os principais conceitos

teoricos e caracterısticas do controle por modos deslizantes.

As principais caracterısticas teoricas de sistemas com atraso sao apresentadas no

capıtulo 4.

A relacao entre estabilidade e LMIs e apresentada no capıtulo 5. Nele e explicitado

o motivo do uso crescente dessa tecnica para garantir a estabilidade de sistemas de

controle.

A tecnica de controle desenvolvida e apresentada com detalhes no capıtulo 6. Sao

apresentadas simulacoes numericas que mostram os resultados obtidos e compravam

a viabilidade da estrategia escolhida.

As conclusoes gerais sobre o estudo desenvolvido sao apresentadas no capıtulo 7.

Por fim, o apendice A apresenta um pequeno tutorial sobre alguns dos pacotes

computacionais existentes para resolucao de LMIs.

4

Capıtulo 2

Conceitos Matematicos

Esse capıtulo tem como objetivo apresentar os conceitos matematicos mais im-

portantes que estao presentes ao longo do texto. Sao eles os conceitos de matrizes

positivas definidas, Complemento de Schur e funcoes de Lyapunov.

As LMIs se integram aos conceitos existentes na teoria de Lyapunov, sendo essa

teoria uma das principais e mais importantes formas de analisar a estabilidade de um

sistema [3, 1]. Como sera explicado adiante, para aplicar corretamente os conceitos

de Lyapunov, e importante entender o que sao matrizes positivas definidas e as

condicoes necessarias para serem caracterizadas como tal. Alem disso, e comum

ser necessario escrever uma inequacao como uma LMI e para isso pode-se usar o

conceito de Complemento de Schur, que tambem e diretamente relacionado com

matrizes positivas definidas.

2.1 Matrizes positivas definidas

Problemas de otimizacao sao comuns em Engenharia. Nesses problemas, normal-

mente precisa-se reconhecer o ponto mınimo de uma funcao. Quando esse ponto

mınimo e a origem, pode-se dizer que a funcao e positiva definida. De forma geral,

uma funcao F (x) e dita positiva definida se:

x 6= 0 ⇒ F (x) > 0, F (0) = 0

Caso F (x) ≥ 0, x 6= 0, a funcao e dita ser positiva semidefinida.

5

Para ilustrar melhor o conceito, considere a princıpio uma funcao quadratica es-

calar simples:

f(x, y) = ax2 + 2bxy + cy2 (2.1)

A funcao (2.1) e definida positiva se, e somente se, a > 0 e ac > b2. E sera definida

negativa se, e somente se, a < 0 e ac > b2. O caso singular ac = b2 leva uma funcao

semidefinida, sendo semidefinida negativa caso a < 0 e semidefinida positiva caso

a > 0 [14].

A funcao (2.1) pode ser escrita na forma matricial, neste caso uma matriz 2× 2:

ax2 + 2bxy + cy2 =[x y

]a b

b c

xy

(2.2)

Essa identidade pode ser generalizada para n dimensoes, como visto em (2.3).

Para qualquer matriz simetrica A, o produto xTAx e uma forma quadratica pura:

[x1 x2 · · · xn

]a11 a12 · · · a1n

a21 a22 · · · a2n

......

. . ....

an1 an2 · · · ann

x1

x2

...

xn

=n∑i=1

n∑j=1

aijxixj (2.3)

A partir da generalizacao acima, pode-se estudar o conceito de matrizes positivas

definidas. Este conceito e extremamente importante para a analise da estabilidade

de sistemas de controle, uma vez que muitas das condicoes de estabilidade partem

do princıpio da existencia de determinada matriz positiva definida.

Considerando a matriz quadrada em (2.3) e chamando ela de A. Esta matriz sera

dita positiva definida caso seja simetrica (A = AT ) e caso satisfaca as condicoes do

teorema abaixo:

Teorema 2.1

6

1. xTAx > 0 para todos os vetores reais x nao nulos.

2. Todos os autovalores de A satisfazem λi > 0.

3. Todas as submatrizes superiores Ak a esquerda tem determinantes positivos.

4. Todos os pivos (sem alteracoes de linha) satisfazem dk > 0.

5. Existe uma matriz R com colunas independentes tais que A = RTR.

Prova: ver [14].

E valido ressaltar que a funcao quadratica xTAx > 0 e de extrema importancia

para a analise de Lyapunov e aparece com bastante frequencia na analise de estabi-

lidade de sistemas de controle.

Para matrizes positivas semidefinidas, o teorema e reescrito da seguinte forma,

tambem considerando uma matriz real A:

Teorema 2.2

1. xTAx ≥ 0 para todos os vetores reais x nao nulos.

2. Todos os autovalores de A satisfazem λi ≥ 0.

3. Nenhuma submatriz principal possui determinantes negativos.

4. Nenhum pivo e negativo.

5. Existe uma matriz R, possivelmente com colunas dependentes, de modo que

A = RTR.

Prova: ver [14].

A definicao de matrizes negativas definidas parte da analogia com matrizes posi-

tivas definidas e o mesmo vale para matrizes negativa semidefinidas com as matrizes

positivas semidefinidas.

7

2.2 Complemento de Schur

O conceito de Complemento de Schur e muito importante no desenvolvimento das

desigualdades matriciais lineares (LMIs). Esta secao tem como objetivo detalhar

melhor esse conceito.

Considere uma matriz quadrada M : n × n escrita como uma matriz com bloco

2× 2:

M =

A B

C D

(2.4)

onde A e uma matriz p× p e D e uma matriz q × q, com n = p+ q, dessa forma

B e uma matriz p× q e C e uma matriz q × p. A matriz M pode ser utilizada para

resolver o seguinte sistema linear:

Ax+By = c

Cx+Dy = d (2.5)

que pode ser reescrito na forma matricial

A B

C D

xy

=

cd

Isolando y e assumindo que D e invertıvel:

y = D−1(d− Cx)

substituindo este resultado em (2.5)

Ax+B(D−1(d− Cx)) = c

(A−BD−1C)x = c−BD−1d

8

Caso A−BD−1C seja invertıvel, a solucao e dada por:

x = (A−BD−1C)−1(c−BD−1d)

y = D−1(d− C(A−BD−1C)−1(c−BD−1d)) (2.6)

A matriz A−BD−1C e chamada de Complemento de Schur de D em M [15]. A

solucao obtida em (2.6) leva a seguinte formula para a inversa de M :

A B

C D

−1

=

(A−BD−1C)−1 −(A−BD−1C)−1BD−1

−D−1C(A−BD−1C)−1 D−1 +D−1C(A−BD−1C)−1BD−1

A B

C D

−1

=

(A−BD−1C)−1 0

−D−1C(A−BD−1C)−1 D−1

I −BD−1

0 I

A B

C D

−1

=

I 0

−D−1C I

(A−BD−1C)−1 0

0 D−1

I −BD−1

0 I

A partir da equacao acima, e possıvel obter uma nova expressao para M , com a

vantagem de que nesta expressao e necessario que apenas D seja invertıvel:

A B

C D

=

I BD−1

0 I

(A−BD−1C) 0

0 D

I 0

D−1C I

A partir desse resultado, e possıvel caracterizar matrizes positivas definidas usando

o Complemento de Schur. Assuma que M seja simetrica, de forma que A e D sejam

simetricas e que C = BT , entao M pode ser reescrita como:

A B

BT D

=

I BD−1

0 I

(A−BD−1BT ) 0

0 D

I BD−1

0 I

T

9

E possıvel definir entao:

Definicao 2.1 Para qualquer matriz M da forma

M =

A B

BT C

Se C e invertıvel entao as seguintes propriedades sao validas:

1. M > 0 se e somente se C > 0 e A−BC−1BT > 0

2. Se C > 0 entao M ≥ 0 se e somente se A−BC−1BT ≥ 0

Prova: Para uma matriz M ser positiva definida e necessario que xTMx > 0. Esta

condicao pode ser escrita da seguinte forma:

xT

M︷︸︸︷ A B

BT C

x > 0

Reescrevendo de forma a obter o Complemento de Schur:

xT

PT︷︸︸︷I −BC−1

0 I

︸︷︷︸

wT

A−BC−1BT 0

0 C

︸︷︷︸

S

P︷︸︸︷ I 0

−C−1BT I

x︸︷︷︸

w

> 0

Dessa forma, obtem-se:

xTMx > 0 ⇔ xTP TSPx > 0

Pode-se reescrever xTP TSPx > 0 como wTSw > 0. Portanto, e necessario que

S > 0:

S =

A−BC−1BT 0

0 C

> 0

10

Da subsecao anterior sabe-se que para uma matriz ser positiva definida, todas as

submatrizes superiores a esquerda devem ter determinante positivo, ou seja, cada

um dos blocos de uma matriz positiva definida deve ser tambem positivo definido

[15]. Dessa forma, obtem-se as condicoes:

C > 0

A−BC−1BT > 0

Essas condicoes estao de acordo com a Definicao 2.1.

2.3 Teoria de Lyapunov

A analise da estabilidade de muitos sistemas, sejam eles lineares ou nao lineares,

muitas vezes se baseia nos metodos de Lyapunov. A teoria de Lyapunov e dividida

em dois metodos: o primeiro se baseia na linearizacao do sistema e analise do sistema

linearizado ao redor de um ponto de equilıbrio, o segundo e mais geral e se baseia no

conceito de energia do sistema, que e analisado por meio de uma funcao, chamada

de funcao de Lyapunov. Como esse trabalho nao ira trabalhar com o metodo da

linearizacao, ele nao sera detalhado aqui e mais informacoes podem ser encontradas

em [3].

Considere o sistema autonomo:

x(t) = f(x(t)), x(0) = x0

Um conceito importante para o entendimento de estabilidade e o de ponto de

equilıbrio, que pode ser entendido da seguinte forma:

Definicao 2.2 Um estado x∗ e um estado de equilıbrio (ou ponto de equilıbrio) de

um sistema se, uma vez que x(t) seja igual a x∗, o estado se mantera igual a x∗

para todo tempo futuro.

Matematicamente isso significa que o estado x∗ satisfaz a seguinte relacao:

f(x∗) = 0 (2.7)

11

Apos definido o conceito de ponto de equilıbrio, e possıvel definir os conceitos de

estabilidade.

Assim como na analise de sistemas lineares, e possıvel estudar o comportamento

de um sistema nao linear na vizinhanca da origem ao inves do ponto de equilıbrio

x∗, o que simplifica bastante a analise da estabilidade do sistema. Dessa forma,

supondo que f possui um ponto de equilıbrio em xe = 0 e denotando BR como a

regiao esferica definida por ||x|| < R no espaco de estados e SR a propria esfera,

definida por ||x|| = R, e possıvel definir os conceitos de estabilidade e instabilidade:

Definicao 2.3 O ponto de equilıbrio xe = 0 e estavel se, para qualquer R > 0, existe

r > 0, tal que se ||x(0)|| < r, entao ||x(t)|| < R para todo t > 0. Caso contrario, o

ponto de equilıbrio e dito instavel.

Essa definicao de estabilidade e conhecida como estabilidade no sentido de Lya-

punov e pode ser entendida da seguinte forma: uma trajetoria do sistema pode ser

mantida arbitrariamente perto do ponto de equilıbrio caso comece perto o suficiente

deste ponto. A definicao 2.3 pode ser escrita como:

∀R > 0,∃r > 0, x(0) ∈ Br ⇒ x(t) ∈ BR, ∀t ≥ 0

Caso as trajetorias do sistema nao satisfacam a condicao de estabilidade ele e dito

como sendo instavel.

Apesar da estabilidade ser uma definicao importante, em muitos sistemas de con-

trole e necessario que o sistema seja assintoticamente estavel. Este tipo de estabili-

dade e definida da seguinte forma:

Definicao 2.4 Um ponto de equilıbrio xe = 0 e assintoticamente estavel se e estavel

e, alem disso, x(t)→ 0 quando t→∞.

12

Um ponto de equilıbrio que e estavel no sentido de Lyapunov, mas nao e assin-

toticamente estavel e conhecido como marginalmente estavel. Alguns problemas

precisam estimar quao rapido as trajetorias vao tender para o ponto de equilıbrio e

a estabilidade exponencial e utilizada para esse proposito:

Definicao 2.5 Um ponto de equilıbrio xe = 0 e exponencialmente estavel se existem

dois numeros estritamente positivos α e λ tais que

||x(t)|| ≤ α||x(0)||e−λt, ∀t > 0

em alguma regiao Br ao redor da origem.

A definicao 2.5 significa que o vetor de estado de um sistema exponencialmente

estavel converge para o ponto de equilıbrio mais rapidamente que uma funcao ex-

ponencial. O numero λ e conhecido como a taxa de convergencia exponencial.

As tres definicoes citadas ate agora caracterizam o comportamento local do sis-

tema, ou seja, o que acontece caso o estado se inicie perto do ponto de equilıbrio.

Para caracterizar o que acontece caso a trajetoria se inicie em algum ponto longe do

equilıbrio e preciso utilizar conceitos de estabilidade globais:

Definicao 2.6 Se a estabilidade assintotica (exponencial) e valida para qualquer

estado inicial, entao o ponto de equilıbrio e globalmente assintoticamente (exponen-

cialmente) estavel.

Figura 2.1: Conceitos de estabilidade.

13

Apos definidos os conceitos de estabilidade e possıvel explicar o segundo metodo

de Lyapunov, que e tambem conhecido como metodo direto de Lyapunov.

A ideia do metodo direto de Lyapunov e uma extensao do conceito de energia

de sistemas: se a energia total de um sistema e continuamente dissipada, entao o

sistema deve eventualmente tender a algum ponto de equilıbrio. Dessa forma, e

possıvel concluir a estabilidade de um sistema analisando a variacao de uma funcao

escalar. O procedimento basico desse metodo e gerar uma funcao escalar para o

sistema, que lembre uma funcao de energia, e examinar a variacao no tempo desta

funcao.

Essas funcoes de energia possuem duas propriedades. A primeira e baseada no

conceito de funcoes positivas definidas. Ja a segunda implica que a funcao e mono-

tonicamente decrescente e e formalizada pelas funcoes de Lyapunov.

Definicao 2.7 Uma funcao escalar V (x) e positiva definida localmente se V (0) = 0

e, em uma regiao BR0

x 6= 0⇒ V (x) > 0

Se V (0) = 0 e a propriedade anterior e valida para todo o espaco de estado, entao

V (x) e positiva definida globalmente.

Definicao 2.8 Se, em uma regiao BR0, a funcao V (x) e positiva definida e possui

derivadas parciais contınuas, alem de possuir derivada no tempo ao longo de qualquer

trajetoria negativa semidefinida, ou seja:

V (x) ≤ 0

esta funcao e uma funcao de Lyapunov para o sistema.

E possıvel relacionar as funcoes de Lyapunov com a estabilidade da seguinte forma:

Teorema 2.3 Se, em uma regiao BR0 existe uma funcao escalar V (x) com deriva-

das parciais contınuas tal que

� V (x) e positiva definida (localmente em BR0)

14

� V (x) e negativa semidefinida (localmente em BR0)

entao o ponto de equilıbrio xe = 0 e estavel. Caso V (x) seja negativa definida

localmente em BR0, entao a estabilidade e assintotica.

Prova: ver [3].

O teorema 2.3 garante apenas a estabilidade local do sistema. Para garantir a

estabilidade global e assintotica e necessario que a regiao BR0 seja o espaco de estado

completo e que V (x)→∞ quando ||x|| → ∞.

Teorema 2.4 Assumindo a existencia de uma funcao escalar V do estado x, com

derivadas de primeira ordem contınuas, tal que:

� V (x) e positiva definida

� V (x) e negativa definida

� V (x)→∞ quando ||x|| → ∞

entao o equilıbrio e globalmente assintoticamente estavel.

Prova: ver [3].

Para ilustrar o metodo de Lyapunov, considere um sistema linear da forma:

x = Ax (2.8)

Escolhendo a funcao quadratica (2.9) como candidata a funcao de Lyapunov:

V (x) = xTPx (2.9)

com P sendo uma matriz positiva definida. Derivando (2.9) ao longo das tra-

jetorias de (2.8):

V (x) = xTPx+ xTPx = xTATPx+ xTPAx = −xTQx (2.10)

ATP + PA = −Q (2.11)

15

Caso a matriz Q, determinada pela equacao de Lyapunov (2.11), seja positiva

definida, a funcao V (x) atendera as condicoes do Teorema 2.4 e o ponto de equilıbrio,

nesse caso, a origem, sera assintoticamente estavel de forma global.

E importante ressaltar que um sistema nao possui apenas uma funcao de Lyapunov

e que uma boa escolha da funcao leva a resultados mais precisos. Alem disso, caso

as condicoes dos teoremas acima nao sejam satisfeitas para uma funcao V (x), nada

pode ser dito sobre a estabilidade do sistema, apenas pode-se tentar realizar uma

nova analise usando uma funcao de Lyapunov diferente.

Apesar de ser um metodo poderoso, o metodo direto de Lyapunov possui uma

desvantagem: encontrar uma funcao de Lyapunov nem sempre e uma tarefa simples.

Por esse motivo existem estudos [2, 1, 16] que visam analisar e escolher as melhores

funcoes de Lyapunov para sistemas com atraso. O metodo de Lyapunov-Krasovskii

para TDS sera explicado com mais detalhes no Capıtulo 5.

16

Capıtulo 3

Controle por Modos Deslizantes

Para sistemas que possuem grandes incertezas, como variacao de parametros,

dinamicas nao modeladas e disturbios externos, existem algumas tecnicas de controle

nao-linear utilizadas para tratarem tais problemas, um exemplo dessas tecnicas e o

controle por modos deslizantes (Sliding Mode Control - SMC ) [3, 17, 18].

No SMC utiliza-se uma lei de controle descontınua que chaveia entre um conjunto

de funcoes das variaveis de estado da planta, de forma a mudar a estrutura do sistema

em malha fechada. Dessa maneira e possıvel combinar caracterısticas uteis de cada

estrutura do sistema realimentado, ou ate mesmo se obter propriedades que nao

estao presentes em nenhuma das estruturas utilizadas [8]. A regra de chaveamento

e elaborada de tal forma que as trajetorias do sistema alcancem e se mantenham em

uma superfıcie do espaco de estados, denominada superfıcie de deslizamento, que e

escolhida pelo projetista.

A principal vantagem desta tecnica de controle e que e possıvel obter um novo

tipo de movimento, denominado modo deslizante, que uma vez que e alcancado, faz

com que o sistema passe a ser regido pela dinamica da superfıcie de deslizamento

[11]. Assim o desempenho do sistema torna-se insensıvel em relacao as incertezas

da planta, propriedade conhecida como propriedade da invariancia. Portanto, essa

tecnica possui aplicacoes em varias areas da engenharia como: robotica, sistemas

espaciais, controle automatico de voos, entre outros [3].

17

Um dos problemas enfrentados pelo controle por modos deslizantes e a possibili-

dade da ocorrencia do chattering, que consiste de um chaveamento em alta frequencia

do sinal de controle. Tal problema e causado devido as imperfeicoes no chaveamento

e e altamente indesejavel, pois pode fazer aparecer dinamicas de alta frequencia ig-

noradas durante a modelagem, instabilizando o sistema [19].

Esse capıtulo tambem apresenta o conceito de controle por modos deslizantes

integral (Integral Sliding Mode Control - ISMC ). Tecnicas baseadas no ISMC pos-

suem uma principal vantagem sobre o SMC tradicional: nelas, o deslizamento ocorre

durante toda a resposta do sistema em malha fechada, com isso garante-se que a

robustez do sistema seja valida durante todo tempo. Alem disso, sera mostrada que,

para escolhas adequadas dos parametros do projeto, o uso do ISMC torna o sistema

menos sensıvel a incertezas descasadas, sendo bastante vantajoso para casos mais

gerais.

3.1 Sistema de Controle Descontınuo

Seja um sistema de controle dado por:

x = a(t, x) + b(t, x)u

onde x ∈ Rn e o vetor de estados do sistema, a(t, x) e b(t, x) sao funcoes suaves

e u ∈ R e uma lei de controle descontınua. Neste projeto, e adotada a definicao

de Filippov para a solucao de equacoes diferenciais com lado direito descontınuo

[20, 21].

A ideia geral do controle por modos deslizantes e primeiramente definir a superfıcie

de deslizamento S = {x : s(x) = 0} de modo que a dinamica desejada seja alcancada

quando o sistema se encontrar dentro da mesma. Posteriormente, deve-se escolher

uma lei de controle descontınua que torne esta superfıcie de deslizamento pelo menos

localmente atrativa, seguindo uma condicao de alcancabilidade.

O sistema deve entao chavear entre duas estruturas diferentes. Essas estruturas

sao definidas de acordo com o sinal de controle descontınuo, que e dado por:

18

u(x) =

u+(x), se s(x) > 0

u−(x), se s(x) < 0

Onde u+(x) e u−(x) sao funcoes contınuas. Note ainda que u(x) nao e definido

em s(x) = 0.

3.2 Nocoes Basicas

Para exemplificar algumas caracterısticas do controle por modos deslizantes, sera

usado um exemplo simples. Considere o sistema:

x1 = x2

x2 = u

u = −f(t) sign(s)

s = x2 + αx1

(3.1)

Considerando α = 1 e f(t) = 5 e possıvel dividir este sistema em duas regioes:

� Na regiao I s(x) > 0, tem-se:

x1 = x2

x2 = −5(3.2)

� Na regiao II s(x) < 0, tem-se:

x1 = x2

x2 = 5(3.3)

Os planos de fase para ambas as regioes seguem abaixo. Para facilitar a visua-

lizacao tambem se encontra representada a reta de chaveamento (s(x) = 0).

19

Figura 3.1: Plano de fase para o sistema (3.2).


E possıvel observar que em ambos os planos de fase, as trajetorias apontam para

a reta de chaveamento. O plano de fase para o sistema completo segue abaixo, assim

como o grafico de x x t.

20


Figura 3.4: Grafico de x x t para o sistema (3.1).

Para o plano de fase do sistema completo, todas as trajetorias tendem para a

reta de chaveamento e a trajetoria do sistema fica confinada a superfıcie deslizante.

Isto gera um novo tipo de movimento, uma vez que essa trajetoria nao pertence a

nenhum dos dois sistemas chaveados. Alem disso, a frequencia de chaveamento se

torna infinita e o sinal de controle passa a nao ser mais definido no tempo.

21

Neste movimento, conhecido como modo deslizante, a trajetoria de estado se des-

loca por uma superfıcie denominada superfıcie de deslizamento, que e denotada por

s(x) = 0. Ja no espaco de estado, o chaveamento ocorre em uma superfıcie denomi-

nada superfıcie de chaveamento. Embora no exemplo citado estas duas superfıcies

sejam as mesmas, isso nem sempre e verdade.

O movimento das trajetorias do sistema e dividido em duas fases. Na primeira

fase, conhecida como fase de aproximacao, a trajetoria iniciada em qualquer lugar

do plano de fase e conduzida em tempo finito para a superfıcie de deslizamento.

Na segunda fase, o sistema entra em modo deslizante e ocorre uma reducao na

ordem da dinamica do sistema, que passa a ser dada pela equacao da superfıcie

de deslizamento. No exemplo analisado, no deslizamento o sistema passa a ser

governado pela seguinte equacao diferencial:

x1 = −x1

A partir desse momento, o sistema apresentara um comportamento igual ao de

um sistema de primeira ordem e tera uma convergencia exponencial para a origem.

Para representar o que acontece com o sinal de controle na presenca de imper-

feicoes, a expressao sign(s) sera substituıda por um rele com histerese. Nesse caso,

para uma histerese de valor mais alto, o sinal de controle nao possui uma frequencia

infinita e as trajetorias nao ficam confinadas perfeitamente na superfıcie de desliza-

mento. Para uma histerese de valor um pouco menor, o sistema se aproxima mais

do ideal, mas ainda ocorre trepidacoes nas trajetorias. Para uma histerese de valor

bem baixo (na faixa dos 0.001), a frequencia de chaveamento fica bastante elevada.

No limite, quando a largura da histerese tender para zero a frequencia tenderia para

o infinito e o sinal de controle nao poderia ser mais definido no tempo. Neste caso,

poderia-se considerar que o sistema entrou em modo deslizante.

22

Figura 3.5: Exemplos de trajetorias proximas da superfıcie de deslizamento e sinais de

controle para um sistema com histerese.

Para ilustrar esse comportamento, tem-se as seguintes figuras. Nas figuras 3.5 (a)

e 3.5 (d) tem-se a trajetoria maxima e o sinal de controle, respectivamente, para

uma histerese de 0.5. Nas figuras 3.5 (b) e 3.5 (e) tem-se as mesmas figuras porem

para uma histerese de 0.05 e nas figuras 3.5 (c) e 3.5 (f) para uma histerese de 0.005.

O fenomeno que ocorre para valores de histerese mais alto e conhecido como chat-

tering, que pode ser explicado da seguinte forma: no modo deslizante ideal, o estado

permanece na superfıcie de deslizamento e o sinal de controle possui frequencia in-

finita, ja no deslizamento real, o sinal de controle oscila em frequencias altas, mas

nao infinitas. Nesse caso, e possıvel ver uma trepidacao nos sinais do sistema.

Um aspecto interessante desse tipo de abordagem e a robustez do controlador.

Mesmo com incertezas ou pertubacoes, se as trajetorias do sistema continuarem

apontando em direcao a superfıcie de deslizamento, o sistema continuara entrando

em modo deslizante e apresentara o mesmo desempenho citado anteriormente (sera

governado pela dinamica referente a equacao da superfıcie de deslizamento).

23

Para ilustrar essa caracterıstica, considere o exemplo a seguir, onde foi colocada

uma pertubacao do tipo senoidal, com α = 1 e f(t) = 5:

x1 = x2

x2 = 4 sin(x1) + u

u = −f(t) sign(s)

s = x2 + αx1

(3.4)

A figura abaixo mostra o plano de fase para o sistema completo e pode ser visto

que mesmo com a pertubacao, as trajetorias continuam apontando na direcao da

superfıcie de deslizamento, o que garante que o sistema entre em modo deslizante.

A partir deste momento o sistema se torna insensıvel a perturbacoes.


3.3 Existencia dos Modos Deslizantes

Para que o sistema entre em modo deslizante, a superfıcie de deslizamento deve

ser pelo menos localmente atrativa, ou seja, deve existir um domınio envolvendo a

superfıcie no qual as trajetorias do sistema apontam na sua direcao. Um criterio

matematico sucinto para expressar esse fato e dado por:

24

ss ≤ 0 (3.5)

A condicao (3.5) e chamada de condicao de alcancabilidade. Entretanto, essa

condicao garante que a superfıcie de deslizamento seja alcancada apenas assintotica-

mente, o que nao e suficiente para assegurar que o sistema entre em modo deslizante.

Para garantir que a superfıcie de deslizamento seja alcancada em tempo finito,

uma condicao mais restritiva deve ser satisfeita. Essa condicao e a condicao de

alcancabilidade-η dada por:

ss ≤ −η|s| (3.6)

onde η e uma constante positiva.

Reescrevendo a equacao (3.6) como

1ds2

2dt≤ −η|s|

ou ainda:

1d(|s|2)

2√

(|s|2)≤ −ηdt

e integrando de 0 a ts, segue que:

|s(ts)| − |s(0)| ≤ −ηts

Deste modo, o tempo necessario para atingir a superfıcie s = 0, representado por

ts, satisfaz:

ts ≤|s(0)|η

o que assegura uma convergencia em tempo finito para a superfıcie de desliza-

mento.

25

Nos casos analisados anteriormente, esta condicao e satisfeita de forma local,

garantido o aparecimento do deslizamento ideal.

� Exemplo 1:

s = x1 + x2

s = x2 − 5 sign(s)

ss ≤ −|s|(5− |x2|)

Dessa forma, para existir o modo deslizante neste caso temos que ter:

5− |x2| ≥ 0

|x2| ≤ 5 (3.7)

� Exemplo 2

s = x1 + x2

s = x2 + 4 sin(x1)− 5 sign(s)

ss ≤ −|s|(5− 4 sin(x1)− |x2|)

1− |x2| ≥ 0

|x2| ≤ 1 (3.8)

26

No caso ideal considerado pelo Exemplo 1, para que o deslizamento seja alcancado

de forma global a seguinte condicao deve ser satisfeita:

f(t) ≥ |x2|+ η

sendo que η e uma constante positiva que pode ser arbitrariamente pequena.

Nos casos analisados, como o deslizamento acontece localmente, quando x2 nao

satisfaz as condicoes acima, a trajetoria ira passar da superfıcie e somente quando

satisfazer as condicoes de deslizamento a trajetoria ficara confinada na superfıcie

de deslizamento. A figura 3.7 ilustra isso para o Exemplo 1, onde nao existe per-

turbacao.

Figura 3.7: Ilustracao do deslizamento local.

3.4 Metodo da Regularizacao

O modo de deslizamento ideal envolve o uso de um sinal de controle descontınuo,

o que impoe algumas dificuldades para a representacao matematica do sistema.

Para contornar esse problema, uma abordagem simples utilizada e a introducao de

imperfeicoes fısicas (zona morta, histerese, atraso) no dispositivo de chaveamento.

Com isto, o modo de deslizamento que apareceria na superfıcie descontınua dara

lugar a trajetorias mais suaves, que sao contınuas por partes.

27

Todavia, essa abordagem possui uma limitacao: deve ser conhecida a natureza

dessas imperfeicoes, o que nem sempre e facil. Uma solucao utilizada para resolver

esse problema e o uso do conceito de camada de fronteira (boundary layer), que per-

mite obter as equacoes do deslizamento sem especificar a natureza das imperfeicoes.

Considere sistemas da seguinte forma:

x = a(x, t) + b(x, t)u (3.9)

E suponha que a superfıcie de deslizamento exista e seja dada por s(x) = 0. A ideia

desse conceito e substituir o controle u, na vizinhanca da superfıcie de deslizamento,

por outro controle u que leve em consideracao todas a imperfeicoes, as encontradas

no dispositivo de chaveamento e as existentes na planta. O movimento do sistema

passa a ser entao:

x = a(x, t) + b(x, t)u

A solucao da equacao regularizada acima resulta em um movimento que nao

ocorre somente sobre a superfıcie de deslizamento (s(x) = 0), mas sim em alguma

vizinhanca

|s(x)| ≤ ∆

onde ∆ e uma constante positiva pequena. Este movimento e denominado desliza-

mento real. Como foi visto na figura 3.5 durante o deslizamento real o chaveamento

do sistema apresenta uma frequencia finita, que representa o fenomeno de chatte-

ring. Este fenomeno e extremamente prejudicial, pois pode excitar modos rapidos

do sistema que haviam sido desprezados, podendo levar o sistema a instabilidade.

Caso as imperfeicoes do sistema tendam para zero, ou seja, caso ∆ → 0 o desli-

zamento real tendera para o deslizamento ideal e a frequencia de chaveamento do

sistema tendera para o infinito, evitando dessa forma o surgimento do chattering.

28

3.5 Metodo do Controle Equivalente

Uma forma alternativa dos modos deslizantes serem representados e pelo conceito

de controle equivalente [10, 11]. Esse metodo consiste em encontrar um controle

contınuo ueq (o controle equivalente), que para uma dada condicao inicial sobre a

superfıcie de deslizamento, a trajetoria dos sistemas (3.9) passa a ser:

x = a(x, t) + b(x, t)ueq (3.10)

Essa trajetoria deve coincidir com a trajetoria descrita pelo sistema a estrutura

variavel durante o deslizamento.

Para encontrar o controle equivalente e suficiente notar que s(x) = 0 e uma

condicao necessaria para que as trajetorias de estado permanecam na superfıcie de

deslizamento s(x) = 0. Derivando s(x) ao longo das trajetorias de (3.9), obtem-se:

s(x) =∂s

∂xa(x, t) +

∂s

∂xb(x, t)u = 0 (3.11)

Resolvendo (3.11) para u, obtem-se o controle equivalente:

ueq = −(∂s

∂xb(x, t)

)−1(∂s

∂xa(x, t)

)(3.12)

onde a existencia de(∂s∂xb(x, t)

)−1e uma condicao necessaria.

O sistema abaixo e usado como exemplo para ilustrar o procedimento:

x1 = x2

x2 = u

u = − sign(s)

s = x1 + 2x2

(3.13)

A figura 3.8 apresenta o plano de fase do sistema (3.13). Vale ressaltar que o

sistema so entra em modo deslizante quando |x2| < 2.

29


Para este caso o controle equivalente e obtido do seguinte modo:

s(x) = x2 + 2u⇒ ueq = −x2

2(3.14)

Substituindo o controle equivalente obtido em (3.14) no sistema (3.13), obtem-se

o seguinte sistema:

x1 = x2

x2 = ueq

ueq = −x22

(3.15)

O sistema (3.15) e equivalente ao sistema (3.13) durante o deslizamento.

A figura 3.9 apresenta o grafico dos sinais x1, x2 e u dos sistemas (3.13) e (3.15),

com a mesma condicao inicial para os dois. Nesta figura pode ser visto que os

sistemas apresentam o mesmo desempenho. Embora o controle equivalente (figura

3.9 (d)) seja contınuo e muito diferente do controle descontınuo (figura 3.9 (c)), ele

pode ser entendido como sendo o comportamento medio deste controle descontınuo.

30

Figura 3.9: (a) Grafico de x x t para o sistema (3.13); (b) Grafico de x x t para o sistema

(3.15); (c) Sinal de controle para o sistema (3.13); (d) Sinal de controle para o sistema

(3.15).

3.6 Controle por Modos Deslizantes Integral

O SMC convencional possui como principal caracterıstica sua robustez contra in-

certezas casadas. Porem, essa caracterıstica importante e alcancada apenas quando

o sistema passa da fase de aproximacao e entra em deslizamento. Dessa forma, du-

rante a fase de aproximacao o sistema fica sujeito ao efeito de qualquer incerteza,

inclusive as casadas.

31

Para contornar esse problema, foi proposto o ISMC. Esse tipo de controle tem

como principal objetivo forcar que ocorra o deslizamento desde o inıcio da resposta

do sistema, de forma que o sistema consiga ser robusto contra incertezas casadas

durante todo o tempo de resposta. Alem disso, sera mostrado adiante que o ISMC

tem a vantagem de nao amplificar o efeito de incertezas descasadas [22].

As subsecoes seguintes visam exemplificar as caracterısticas do ISMC por meio

do projeto do controle baseado no ISCM de um sistema LTI incerto. Os desen-

volvimentos dessa secao sao baseados nos desenvolvimentos apresentados em [22].

Assume-se durante toda essa secao que a informacao sobre o vetor de estados esta

disponıvel para o projeto do controlador. Alem disso, no ISMC assume-se que existe

uma planta nominal, na qual um controlador apropriado ja foi projetado para garan-

tir a estabilidade assintotica do sistema em malha fechada. Assim, um controlador

descontınuo e ‘adicionado‘ ao controlador nominal de forma a manter a performance

nominal e garantir que o sistema seja insensıvel a perturbacoes externas.

3.6.1 Definicao do Problema

Considere o seguinte sistema:

x(t) = Ax(t) +Bu(t) +Mξ(t, x) + fu(t, x) (3.16)

onde A ∈ Rn×n, B ∈ Rn×m. Assume-se que a matriz B possui posto completo,

ou seja, posto(B) = m, onde 1 ≤ m < n e que o par (A,B) e controlavel. Alem

disso, assume-se que a matriz M ∈ Rn×l e conhecida e se encontra na extensao do

espaco da matriz de distribuicao de entrada B, sendo possıvel escrever M = BD

para algum D ∈ Rm×l. Dessa forma, o sistema (3.16) pode ser reescrito, como:

x(t) = Ax(t) +Bu(t) +BDξ(t, x) + fu(t, x) (3.17)

Incertezas da forma BDξ(t, x), que agem no canal da matriz de distribuicao de

entrada, sao conhecidas como incertezas casadas. Ja o termo fu(t, x) representa

uma incerteza descasada, ou seja, que nao esta na extensao do espaco da matriz B.

32

No problema considerado, assume-se que a incerteza descasada e limitada com um

limite superior conhecido [22].

O sistema nominal associado ao sistema (3.17) pode ser escrito como:

x(t) = Ax(t) +Buo(t) (3.18)

Onde uo(t) e a lei de controle nominal, que pode ser projetada por meio de qual-

quer paradigma de realimentacao de estado capaz de atingir a performance nominal

desejada [22]. Como se assume que o par (A,B) e controlavel, existe um controle

de realimentacao de estado da seguinte forma:

uo(t) = −Fx(t) (3.19)

Onde F ∈ Rm×n e o ganho da realimentacao a ser projetado, de forma que as

trajetorias de estado do sistema nominal (3.18), chamadas de xo(t), sao estaveis e

respeitam as especificacoes de performance. O objetivo e desenvolver uma lei de

controle u(t), tal que as trajetorias de estado x(t) de (3.16) durante o deslizamento

satisfacam a condicao x(t) ≡ xo(t) para todo o tempo se fu(.) = 0, partindo do

tempo inicial onde x(0) ≡ xo(0). Para atingir x(0) ≡ xo(0) a ordem do sistema

em deslizamento deve ser a mesma do sistema nominal, sendo essa uma primeira

diferenca para o SMC tradicional, onde a ordem do sistema em deslizamento e

reduzida.

3.6.2 Princıpios do Projeto

Definindo a lei de controle u(t) com a forma:

u(t) = uo(t) + un(t) (3.20)

Onde uo(t) e o controle nominal e un(t) e um termo nao linear incluıdo para

induzir o modo deslizante. Utilizando (3.20), a equacao do sistema (3.16) pode ser

reescrita como:

33

x(t) = Ax(t) +Buo(t) +Bun(t) +BDξ(t, x) + fu(t, x) (3.21)

O termo un(t) e escolhido de forma a rejeitar a perturbacao ξ(t, x) enquanto o

sistema estiver no deslizamento e uo(t) e dado pela equacao (3.19). A superfıcie de

deslizamento e definida como:

s(t) = Gx(t) + z(t) (3.22)

G ∈ Rm×n e z(t) e especificada. A matriz de deslizamento G pode ser escolhida

de forma que a matriz GB seja nao singular (det(GB) 6= 0). Durante o deslizamento

s(t) = s(t) = 0 e portanto:

s(t) = Gx(t) + z(t) = 0 (3.23)

Para garantir que o controle equivalente associado com un(t) rejeite o efeito da

perturbacao casada ξ(t, x) (quando fu(t, x) = 0) e que a condicao x(t) ≡ xo(t) seja

satisfeita para todo t > 0, substitui-se o valor de (3.21) em (3.23):

s(t) = G(Ax(t) +Buo(t) +Bun(t) +BDξ(t, x)) + z(t) = 0 (3.24)

Durante o deslizamento espera-se que un(t) compense a incerteza, portanto espera-

se que uneq = −Dξ(t, x). Dessa forma, pode-se escolher:

z(t) = −G(Ax(t) +Buo(t)), z(0) = −Gx(0) (3.25)

Essa escolha garante que

s(t) = GBun(t) +GBDξ(t, x) (3.26)

E portanto durante o deslizamento uneq = −Dξ(t, x). Substituindo o valor de uneq

em (3.21) e possıvel notar que na ausencia da perturbacao fu(t, x) o modo deslizante

integral e governado por:

34

x(t) = Ax(t) +Buo(t) (3.27)

A equacao (3.27) confirma que a condicao x(t) ≡ xo(t) e satisfeita se fu(t, x) = 0

e x(0) = xo(0). Para o caso onde fu(t, x) 6= 0, o controle equivalente pode ser obtido

da equacao (3.24):

uneq(t) = −(GB)−1GBDξ(t, x)− (GB)−1Gfu(t, x)

= −Dξ(t, x)− (GB)−1Gfu(t, x) (3.28)

Substituindo este valor de uneq(t) em (3.21), e possıvel obter uma expressao para

a dinamica do modo de deslizamento integral:

x(t) = Ax(t) +Buo(t) + (I −B(GB)−1G)︸︷︷︸Γ

fu(t, x) (3.29)

Pela equacao (3.29) fica claro que o efeito da incerteza casada foi completamente

rejeitado durante o deslizamento. Porem, a matriz Γ pode amplificar os efeitos da

incerteza descasada fu(t, x). Portanto, e necessario projetar a superfıcie de desliza-

mento integral de forma a evitar qualquer amplificacao da incerteza descasada.

3.6.3 Superfıcie de Deslizamento Integral

Usando as expressoes (3.22) e (3.25), obtem-se uma expressao para a superfıcie

de deslizamento integral que elimina a fase de aproximacao:

s(t) = Gx(t)−Gx(0)−G∫ t

0

(Ax(τ) +Buo(τ)) dτ (3.30)

O termo −Gx(0) vem do fato de z(0) = −Gx(0) e e ele que garante que s(0) = 0,

fazendo com que a fase de aproximacao seja eliminada. Assim, o modo deslizante

vai existir desde o tempo t = 0 e o sistema sera robusto contra incertezas casadas

por toda a resposta em malha fechada.

35

Para rejeitar incertezas casadas, qualquer escolha de G que garante que GB seja

invertıvel e suficiente, todavia para rejeitar incertezas descasadas e necessario uma

escolha especıfica de G. Uma escolha apropriada e G sendo a pseudo inversa de B:

G = B+ =(BTB

)−1BT (3.31)

Essa escolha para G possui duas vantagens:

1. o ganho de modulacao associado com un(t) em (3.20) e minimizado, o que

significa que a amplitude do fenomeno de chattering pode ser reduzida;

2. evita que perturbacoes descasadas sejam amplificadas.

Essa escolha de G garante que GB e nao singular e simplifica a expressao:

GB =(BTB

)−1BT︸︷︷︸

G

B = Im

Alem disso, essa escolha de G faz com que o operador Γ em (3.29) passe a ser:

Γ = In −B(BTB

)−1BT (3.32)

E importante notar que o operador Γ em (3.32) possui a propriedade Γ2 = Γ.

Esta propriedade implica que ‖Γ‖ = 1, significando, portanto, que o efeito de fu nao

e amplificado ja que ‖Γfu‖ ≤ ‖fu‖.

3.6.4 Leis de controle

O controlador sera projetado baseado no sistema nominal (3.18) e tem a estrutura

dada pela equacao (3.20), com o termo uo(t) sendo a parte linear do controlador e

un(t) sendo a parte descontınua que forca o modo deslizante sobre a superfıcie de

deslizamento (3.30). Uma possıvel escolha para u(t) e:

u(t) = −Fx(t)− ρ(t, x)(GB)−1 s(t)

‖s(t)‖para s(t) 6= 0 (3.33)

36

Onde F e responsavel pela performance do sistema nominal e ρ(t, x), que tera seu

valor definido na proxima subsecao, e a modulacao que garante o modo deslizante.

3.6.5 Condicao de Alcancabilidade

Para garantir a existencia do modo deslizante ideal e necessario que o controlador

(3.33) satisfaca a condicao de alcancabilidade-η. Pode-se escrever:

s(t) = G (Ax(t) +Bu(t) +BDξ(t, x) + fu(t, x))−GAx(t) +GBFx(t) (3.34)

Substituindo (3.33) em (3.34) e simplificando obtem-se:

s(t) = G

(Ax(t) +B

(−Fx(t)− ρ(t, x)(GB)−1 s(t)

‖s(t)‖

)+BDξ(t, x) + fu(t, x)

)−GAx(t) +GBFx(t)

= −ρ(t, x)s(t)

‖s(t)‖+GBDξ(t, x) +Gfu(t, x) (3.35)

A condicao de alcancabilidade-η, ss ≤ η |s| pode ser reescrita como sT s ≤ η ‖s‖.

Dessa forma, multiplicando (3.35) por sT :

sT (t)s(t) = −ρ(t, x)‖s‖2

‖s‖+ sT (t) GB︸︷︷︸

I

Dξ(t, x) + sT (t)Gfu(t, x)

= −ρ(t, x) ‖s(t)‖+ sT (t)Dξ(t, x) + sT (t)Gfu(t, x)

≤ ‖s(t)‖ (−ρ(t, x) + ‖Dξ(t, x)‖+ ‖Gfu(t, x)‖) (3.36)

O valor da modulacao ρ(t, x) deve ser maior que qualquer perturbacao ou incerteza

do sistema, portanto, ρ(t, x) devera satisfazer:

ρ(t, x) ≥ ‖D‖ ‖ξ(t, x)‖+ ‖G‖ ‖fu(t, x)‖+ η (3.37)

Em (3.37), η e um escalar positivo. Com essa escolha para ρ(t, x), a condicao de

alcancabilidade-η e satisfeita e pode ser escrita como:

sT (t)s(t) ≤ −η ‖s(t)‖ (3.38)

37

3.6.6 Propriedades

Por fim, e valido ressaltar as principais caracterısticas do ISMC:

� o deslizamento ocorre durante toda a resposta do sistema, uma vez que a fase

de aproximacao e eliminada;

� durante o deslizamento, a ordem do movimento e a mesma ordem do sistema

original;

� o efeito da incerteza descasada nao e amplificado, com uma escolha correta da

superfıcie de deslizamento;

� durante o deslizamento, o sistema e invariante a incertezas casadas.

Portanto, esse trabalho utiliza o conceito do ISMC, pois com ele e possıvel lidar

com sistemas que alem de incertezas casadas, possuem incertezas descasadas, elimi-

nando, dessa forma, a necessidade de restringir os sistemas a serem controlados aos

casos onde as incertezas encontradas sao casadas.

3.7 Chattering

Como ja foi citado anteriormente, o fenomeno de chattering e uma das principais

desvantagens existentes no controle por modos deslizante. Ele ocorre quando a

superfıcie de deslizamento s(x) = 0 e alcancada e ocorre a excitacao de dinamicas nao

modeladas, que podem levar a oscilacoes do vetor de estados em altas frequencias.

Estas oscilacoes resultam numa reducao da acuracia do controle, o que pode levar

ate mesmo o sistema a instabilidade, dessa forma existe um grande interesse no

estudo e na reducao de seus efeitos [23].

A maneira mais imediata de amenizar o chattering e substituir a nao linearidade

do tipo rele do controlador por um elemento que implemente uma funcao similar,

mas que nao apresente um ponto de descontinuidade, ou seja, a ideia e utilizar uma

aproximacao contınua do rele.

38

Em [19], sao citados varios metodos para lidar com o chattering, onde vale a pena

destacar o metodo que utiliza o conceito de controle equivalente. Em [24], e valido

destacar o metodo do boundary layer. Esta solucao possui um bom desempenho e e

implementada fazendo uso de uma funcao de saturacao. Dessa forma, um controle

da seguinte forma:

u(t) = f(t) sign(s(t))

passa a ser descrito como:

u(t) = f(t) sat

(s(t)

σ

)onde s(t) e a superfıcie de deslizamento e σ e a espessura da boundary layer.

As funcoes sign e sat sao definidas como:

sign(s(t)) =

1, se s(t) > 0

0, se s(t) = 0

−1, se s(t) < 0

sat

(s(t)

σ

)=

1, se s(t) > σ

s(t)σ, se ‖s(t)‖ ≤ σ

−1, se s(t) < −σ

A figura 3.10 mostra como fica o sinal de controle usando a funcao de saturacao.

39

Figura 3.10: Sinal de controle: (a)Rele; (b)Saturacao para σ = 1.

40

Capıtulo 4

Sistemas com atraso

4.1 Introducao

Sistemas com atraso (Time Delay Systems - TDSs), tambem conhecidos como

sistemas com tempo morto, sao extremamente comuns na pratica, dado que nor-

malmente existe um tempo para adquirir a informacao necessaria para a tomada

de decisoes e para a execucao das mesmas. Eles pertencem a classe de equacoes

diferenciais funcionais (Functional Differential Equations - FDEs), que sao sistemas

com dimensao infinita, em oposicao as equacoes diferenciais ordinarias (Ordinary

Differential Equations - ODEs) [2].

Um exemplo simples de TDS e:

x(t) = −x(t− h), x(t) ∈ R (4.1)

onde h > 0 representa o atraso.

Atrasos podem aparecer no estado, na entrada de controle ou na saıda, sendo que

esses atrasos podem ser de transporte, comunicacao ou de medida. Eles aparecem

em uma serie de sistemas de controle, como: controle de aeronaves, controle de

processos quımicos, controle de redes de comunicacao, entre outros [2, 25, 1].

41

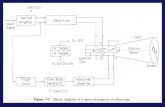
Figura 4.1: Esquematico de um sistema simples com atraso.

A figura 4.1 representa um exemplo de sistema com atraso bem comum e simples.

A pessoa tomando banho deseja atingir a temperatura Td e para isso realiza o ajuste

da temperatura alternando entre colocar a agua mais fria ou mais quente. No tempo

t, a pessoa sente a temperatura da agua que saiu do chuveiro em um tempo anterior

t− h, entao e obtida a seguinte equacao, com h sendo um atraso constante:

T (t) = −k[T (t− h)− Td], k ∈ R (4.2)

Apesar da simplicidade do sistema, o atraso impoe algumas dificuldades. Consi-

dere a funcao de transferencia do sistema (4.2):

G(s) =T (s)

Td(s)=

k

s+ ke−sh

O termo destacado e−sh representa o efeito do atraso no sistema. Esse termo e

uma funcao irracional, o que faz com que seja necessario o uso de aproximacoes

para facilitar o uso de softwares de analise numerica como o Matlab, sendo as mais

comuns a serie de Taylor e Aproximacao de Pade [26, 25].

42

Figura 4.2: Diagrama de Bode para o termo de atraso puro.

Para representar graficamente o efeito do atraso em um sistema, considere o dia-

grama de Bode do atraso puro na figura 4.2. Pela figura e possıvel ver que, apesar de

o atraso nao alterar a magnitude do diagrama de Bode, ele altera a fase, que passa

a decair linearmente com o atraso. Desta forma, o ganho dos controladores que

trabalham com sistemas com atraso sao limitados e costumam ser valores baixos.

Para ilustrar melhor a questao do ganho baixo em sistemas com atraso, considere

o seguinte sistema:

x(t) = x(t− h) (4.3)

O sistema (4.3) possui a seguinte funcao de transferencia:

G(s) =e−sh

s(4.4)

Considerando a possibilidade de um ganho proporcional, a figura 4.3 ilustra a

resposta ao degrau do sistema (4.3) em malha fechada, com atraso h = 1. Como

e possıvel ver, para ganhos K = 2 e K = 1.5, o sistema e instavel. Para um

ganho K = 0.8, o sistema e estavel. Isso demonstra para um exemplo simples como

sistemas com atraso costumam trabalhar com ganhos muito baixos.

43

Figura 4.3: Resposta ao degrau do sistema (4.3) considerando a possibilidade de um

ganho proporcional.

E valido ressaltar que tecnicas baseada em controle por modos deslizantes costu-

mam trabalhar com ganhos altos, portanto a tecnica que sera implementada tera

que lidar com isso para obter bom resultado.

4.2 Conceito de solucao

Considere sistemas com atraso como descritos na equacao (4.1). Para definir a

solucao em t ∈ [0, h], e necessario definir o lado direito da equacao para o mesmo

intervalo de tempo, o que resulta em uma funcao para o valor inicial:

x(θ) = ϕ(θ), θ ∈ [−h, 0] (4.5)

Essa e uma das diferencas para as ODEs, ao inves de existir uma condicao inicial

x(0) em h = 0 como existe nas ODEs, existe uma funcao para um intervalo de

tempo como valor inicial para equacao. Outra diferenca e que no caso de ODEs, o

estado e um vetor de n dimensoes se movendo no espaco Rn. Ja as FDEs possuem

a influencia do tempo passado, de forma que o estado nao pode ser mais um vetor

definido no instante t apenas e passa a existir uma quantidade variada de solucoes

que levam ao mesmo valor em um numero infinito de pontos.

Para encontrar uma solucao para o problema, um metodo possıvel de ser utilizado

e o metodo dos passos (step method) [2, 25]. Considerando ainda sistemas como o

44

da equacao (4.1), com condicoes iniciais como na equacao (4.5), primeiro e preciso

achar uma solucao em t ∈ [0, h]:

t ∈ [0, h]→ dx

dt= −ϕ(t− h) ∴

∫ x(t)

ϕ(0)

dx = −∫ t

0

ϕ(τ − h)dτ

x(t) = ϕ(0)−∫ t

0

ϕ(τ − h)dτ︸︷︷︸ϕ1(t)

Continuando o procedimento para t ∈ [h, 2h]:

t ∈ [h, 2h]→ dx

dt= −ϕ1(t− h) ∴

∫ x(t)

ϕ1(h)

dx = −∫ t

h

ϕ1(τ − h)dτ

x(t) = ϕ1(h)−∫ t

h

ϕ1(τ − h)dτ︸︷︷︸ϕ2(t)

Para obter a solucao, continua-se este procedimento para t ∈ [2h, 3h], t ∈ [3h, 4h]

e assim por diante. Para ilustrar melhor o procedimento, considere a equacao (4.1)

com h = 1 e com condicao inicial ϕ = 1:

t ∈ [0, 1]→ dx

dt= −ϕ(t− 1) ∴

∫ x(t)

ϕ(0)

dx = −∫ t

0

ϕ(τ − 1)dτ

x(t) = ϕ(0)−∫ t

0

1dτ︸︷︷︸ϕ1(t)

∴ x(t) = 1− t = ϕ1(t)

t ∈ [1, 2]→ dx

dt= −ϕ1(t− 1) ∴

∫ x(t)

ϕ1(1)

dx = −∫ t

1

ϕ1(τ − 1)dτ

x(t) = ϕ1(1)−∫ t

1

ϕ1(τ − 1)dτ︸︷︷︸ϕ2(t)

x(t) = 0−∫ t

1

1− (τ − 1)dτ = −∫ t

1

2− τdτ

x(t) =t2

2− 2t+

3

2= ϕ2(t)

O procedimento pode ser continuado para mais intervalos de tempo. A figura 4.4

mostra o resultado obtido com o metodo dos passos para o sistema (4.1), com h = 1

e com os valores ϕ = 1 e ϕ = 0.5t para as funcoes que sao as condicoes iniciais.

45

Essa figura ilustra outra caracterıstica das FDEs, uma FDE possui varias solucoes

que levam ao mesmo valor x(t∗) em instantes t∗, em oposicao as ODEs em que em

cada x(t∗) so passa apenas uma solucao. Portanto, em TDSs, o estado e na verdade

uma funcao:

xt : [−h, 0]→ R : xt(θ) = x(t+ θ), θ ∈ [−h, 0]

no intervalo [t− h, t].

Figura 4.4: Solucao do sistema (4.1).

Para ilustrar um caso um pouco mais geral, porem ainda escalar, considere a

seguinte equacao:

x = −a1x(t) + a2x(t− h)

x(t) = ϕ0(t), t ∈ [−h, 0](4.6)

Como ja foi citado, primeiro e necessario encontrar a solucao em t ∈ [0, h]:

t ∈ [0, h]→ x(t) = e−a1tϕ0(0) +

∫ t

0

e−a1(t−τ)a2ϕ0(τ − h)dτ︸︷︷︸ϕ1(t)

Entao, deve-se continuar com os outros intervalos t ∈ [h, 2h], t ∈ [2h, 3h] e assim

por diante:

46

t ∈ [h, 2h]→ x(t) = e−a1(t−h)ϕ1(h) +

∫ t

h

e−a1(t−τ)a2ϕ1(τ − h)dτ︸︷︷︸ϕ2(t)

t ∈ [2h, 3h]→ x(t) = e−a1(t−2h)ϕ2(2h) +

∫ t

2h

e−a1(t−τ)a2ϕ2(τ − h)dτ︸︷︷︸ϕ3(t)

De forma geral: Supondo que x(t) = ϕi−1(t) em um intervalo [ti − h, ti]. Entao,

no intervalo [ti, ti + h], tem-se que:

x(t) = ea1(t−ti)ϕi−1(ti) +

∫ t

ti

e−a1(t−τ)a2ϕi−1(τ − h)dτ︸︷︷︸ϕi(t)

(4.7)

Como e possıvel ver, o resultado obtido em (4.7) e uma generalizacao do caso sim-

ples representado pela equacao (4.1). Para ilustrar o resultado, considere o seguinte

sistema:

x = −2x(t) + x(t− 1)

x(t) = ϕ0(t), t ∈ [−1, 0](ϕ0(t) = 1

2

) (4.8)

Resolvendo a equacao (4.8) se baseando em (4.7):

t ∈ [0, 1]→ x(t) = −2x(t) +1

2

x(t) = e−2t ϕ0(0)︸︷︷︸12

+

∫ t

0

1

2e−2(t−τ)dτ

x(t) =1

2e−2t +

1

4e−2t

[e2τ∣∣∣t0

]

x(t) =1

2e−2t +

1

4− 1

4e−2t ∴ x(t) = ϕ1(t) =

1

4+

1

4e−2t

47

Seguindo para o proximo intervalo t ∈ [1, 2]:

t ∈ [1, 2]→ x(t) = −2x(t) +1

4+

1

4e−2(t−1)

x(t) = e−2(t−1)ϕ1(1) +

∫ t

1

e−2(t−τ)

(1

4+

1

4e−2(τ−1)

)dτ

x(t) =1

4e−2t +

1

4e−2(t−1) +

1

4e−2t

(∫ t

1

e2τdτ +

∫ t

1

e2dτ

)

x(t) =1

4e−2t +

1

4e−2(t−1) +

1

4e−2t

1

2e2τ∣∣∣t1︸︷︷︸

12

(e2t−e2)

+ e2τ∣∣∣t1︸︷︷︸

te2−e2

x(t) =1

4e−2t +

1

4e−2(t−1) +

1

8− 1

8e−2(t−1) +

1

4te−2(t−1) − 1

4e−2(t−1)

x(t) =1

4e−2t +

1

8− 1

8e−2(t−1) +

1

4te−2(t−1)

O processo poderia continuar para mais intervalos de tempo seguindo esse mesmo

raciocınio e tem seu resultado ilustrado na figura 4.5.

Figura 4.5: Solucao do sistema (4.8).

O caso mais geral considera a possibilidade dos escalares a1 e a2 serem matrizes

e possui a seguinte forma:

x(t) = Ax(t) + A1x(t− h) + f(t), t ≥ 0 (4.9)

48

Onde A e A1 sao matrizes constantes, f(t) e uma funcao localmente integravel e

a condicao inicial e definida como em (4.5). A solucao de (4.9) com A1 = 0 e dada

por:

x(t) = eAtϕ(0) +

∫ t

0

eA(t−τ)f(τ)dτ (4.10)

Para considerar o caso onde A1 6= 0, e necessario definir uma matriz X(t) que

satisfaz a equacao homogenea:

x(t) = Ax(t) + A1x(t− h) (4.11)

A matriz X(t) possui as seguintes condicoes iniciais:

X(t) =

0, t < 0

I, t = 0(4.12)

A solucao de (4.9) e dada por:

x(t) = X(t)ϕ(0) +

∫ 0

−hX(t− θ − h)A1ϕ(θ)dθ +

∫ t

0

X(t− τ)f(τ)dτ (4.13)

A prova para o resultado (4.13) pode ser encontrada em [2].

Como e possıvel ver, a solucao de um TDS vai ficando mais complexa conforme se

generaliza o sistema. Dessa forma, o caso mais geral que sera considerando adiante

na estrategia de controle desenvolvida possui uma grande complexidade matematica,

tornando o projeto do controlador mais desafiador.

4.3 Tipos de atrasos

Um sistema com atraso pode estar sujeito a atrasos de naturezas diferentes, sendo

os mais comuns citados nas subsecoes a seguir.

49

4.3.1 Atrasos Constantes

Foram os primeiros tipo de atraso a serem considerados. Os estudos de esta-

bilidade desses sistemas eram baseados principalmente em abordagens no domınio

da frequencia, com destaque para criterios aplicados a funcoes de transferencia de

Laplace. Ja no domınio do tempo, o metodo mais comum utilizado, e que ainda

persiste nos estudos atuais, e o metodo direto de Lyapunov [27, 28].

A analise da estabilidade utilizando o segundo metodo de Lyapunov pode levar a

condicoes que sao ditas independentes do atraso ou dependentes do atraso. Como

o nome sugere, condicoes dependentes do atraso significam que a estabilidade e

garantida apenas para alguns valores de atraso [27].

O crescente numero de estudos baseado no domınio do tempo se deve ao fato de

que os problemas tratados podem ser modelados como LMIs e que estas podem ser

resolvidas de forma simples e eficaz utilizando software de analise numerica, como

por exemplo o Matlab [27].

4.3.2 Atrasos variantes no tempo

Atrasos constantes costumam ser muito restritivos e com o avanco de aplicacoes

na area de redes de comunicacao houve uma motivacao para estudos que consideram

atrasos que variam com o tempo [27, 28].

Atrasos deste tipo sao mais prejudiciais a estabilidade do sistema do que os atrasos

constantes e quanto mais rapida for a variacao do atraso, mais prejudicial e o atraso

[28]. Muitos autores consideram a seguinte suposicao para facilitar o estudo do

sistema:

0 ≤ h(t) ≤ h2 (4.14)

onde h2 e um escalar positivo.

Entretanto, essa suposicao pode ser muito restritiva, pois e permitido que a funcao

de atraso chegue a zero, o que na pratica significaria que transporte da informacao

50

acontece de forma arbitrariamente rapida, e em algumas aplicacoes a velocidade e

limitada [27]. Por conta disso, a suposicao (4.14) e reescrita como:

0 < h1 ≤ h(t) ≤ h2 (4.15)

onde h1 e h2 sao escalares positivos.

Alem dessas suposicoes e muito comum existirem condicoes sobre a derivada da

funcao de atraso. A mais comum e:

h(t) ≤ d ≤ 1 (4.16)

A suposicao (4.16) exemplifica uma classe importante de atrasos variantes no

tempo: os atrasos que variam lentamente com o tempo. Alem disso, essa suposicao

implica que a funcao que representa a evolucao da informacao com atraso no tempo,

f(t) = t− h(t), so pode aumentar. Isso significa que a informacao afeta os sistemas

de forma cronologica [27]. Essa suposicao pode ser generalizada para:

d1 ≤ h(t) ≤ d2 (4.17)

onde d2 nao e necessariamente menor que 1. Essa generalizacao e necessaria

quando as condicoes para estabilidade dependem linearmente da derivada do atraso

[27].

Por fim, no caso da analise de sistemas onde ocorre amostragem de dados, e

comum existir a seguinte suposicao:

h(t) ≤ 1 (4.18)

A suposicao (4.18) implica que a funcao f(t) = t− h(t) pode ser constante, o que

significa que a informacao e mantida quando h(t) = 1, que e exatamente o efeito da

amostragem [27].

51

4.4 Tipos de TDSs

Como foi visto, TDSs se encaixam na classe de FDEs. Todavia, nao existe apenas

um tipo de sistema com atraso. Em relacao ao tipo de atraso que existe no sistema

e possıvel separar os TDSs em dois:

1. Sistemas com atraso discreto

2. Sistemas com atraso distribuıdo

Sistemas com atraso discreto sao sistemas representados pela seguinte FDE:

x(t) = Ax(t) + Adx(t− h), ∀t ≥ 0

x(t) = ϕ(t), ∀t ∈ [−h, 0](4.19)

onde x(t) e o vetor de estados e ϕ e a funcao de condicao inicial. No caso mais

simples pode-se assumir que A e Ad sao matrizes constantes.

A equacao (4.19) representa uma equacao de um TDS com atraso discreto, pois

apenas um valor discreto da funcao de estado, neste caso x(t− h), afeta a dinamica

do sistema. Esse tipo de sistema com atraso aparece em problemas de redes de

comunicacao, na area de Biologia e no controle de trafego por exemplo [27, 28].

Ja os sistemas com atraso distribuıdo sao sistemas onde toda funcao de estado xt

afeta a dinamica atual do sistema e podem ser modelados da seguinte forma:

x(t) = Ax(t) +

∫ 0

−hAd(θ)x(t+ θ)dθ, ∀t ≥ 0

x(t) = ϕ(t), ∀t ∈ [−h, 0]

(4.20)

Como visto em (4.20), valores antigos do estado influenciam a evolucao do sistema

por meio de uma soma contınua (integral). Esse tipo de sistema e comumente

encontrado em sistemas de foguetes, analise de epidemias, entre outras aplicacoes

[28].

52

De forma mais geral, um sistema linear invariante no tempo (Linear Time-Invariant

- LTI ) com atraso pode ser modelado da seguinte maneira:

x(t) =

q∑l=1

Dlx(t− ωl) +k∑i=0

(Aix(t− hi) +Biu(t− hi))

+r∑j=1

∫ t

t−τj(Gj(θ)x(θ) +Hj(θ)u(θ)) dθ (4.21)

y(t) =k∑i=0

Cix(t− hi) +r∑j=1

∫ t

t−τjNj(θ)x(θ)dθ (4.22)

Em (4.21), quando h0 = 0, A0 representa o ganho instantaneo de feedback. Ai(i >

0) representa o efeito dos atrasos discretos, enquanto a soma das integrais representa

o efeito dos atrasos distribuıdos. As matrizes Di correspondem a parte neutra do

sistema. Bi e Hj sao as matrizes de entrada. Em (4.22), y(t) ∈ R e a saıda do

sistema, com Ci representando a parte dos atrasos discretos e Nj representa a parte

dos atrasos distribuıdos.

Considerando sistemas como os da equacao (4.21), com relacao ao tipo de equacao

diferencial, eles podem ser divididos em dois tipos:

1. Equacoes diferenciais retardadas (Retarded Differential Equations - RDEs)

2. Equacoes diferenciais neutras (Neutral Type Differential Equations - NDEs)

A equacao (4.23) e um exemplo de uma RDE, enquanto (4.24) e um exemplo de

NDE.

x(t) = ax(t− h) + bx(t), x(t) ∈ R (4.23)

x(t) = ax(t− h) + bx(t), x(t) ∈ R (4.24)

De forma geral, RDEs sao representadas como na equacao (4.25) e NDEs sao

representadas como em (4.26). Como foi visto na figura 4.4, que ilustra o metodo

dos passos para uma RDE, existe um efeito suavizante na solucao do sistema. Este

53

efeito nao e mais verdadeiro nas NDEs, pois a derivada x(t) pode replicar qualquer

irregularidade da condicao inicial, o que torna difıcil de aplicar o metodo dos passos

a esse tipo de sistemas [25].

x(t) = f(t, xt, ut) (4.25)

x(t) = f(t, xt, xt, ut) (4.26)

Devido as dificuldades impostas pelas NDEs, esse trabalho vai lidar apenas com

RDEs. Alem disso, sistemas com atrasos distribuıdos sao mais difıceis de serem

analisados e controlados e, portanto, tambem nao serao abordados nesse trabalho.

54

Capıtulo 5

Estabilidade e Desigualdades

Matriciais Lineares

5.1 LMIs

Este capıtulo visa explicitar como a analise da estabilidade de TDSs e feita utili-

zando LMIs. Para isto, e necessario definir o que e uma LMI.

LMIs sao desigualdades matriciais que sao lineares em um conjunto de variaveis.

Estas variaveis podem ser um conjunto de vetores no espaco Rn, por exemplo.

Porem e muito comum ter matrizes como variaveis. Essencialmente, LMIs sao res-

tricoes (constraints) convexas. Portanto, problemas descritos por LMIs sao proble-

mas convexos de otimizacao. Esses problemas de otimizacao podem ser resolvidos

de forma eficiente, utilizando pacotes especializados na resolucao de LMIs, nor-

malmente conhecidos como programacao semidefinida (Semidefinite Programming -

SDP) [29, 30]. Detalhes de alguns dos Toolboxs utilizados para a resolucao de LMIs

se encontram no Apendice A.

Uma LMI tem a seguinte forma geral:

F (x) =m∑i=1

xiFi > 0 (5.1)

onde x ∈ Rn e a variavel e as matrizes simetricas Fi ∈ Rn×n sao conhecidas. A

inequacao (5.1) significa que F (x) e positiva definida, uTF (x)u > 0.

55

A inequacao (5.1) representa uma LMI estrita, porem tambem existem LMIs nao

estritas, que possuem a seguinte forma:

F (x) ≥ 0 (5.2)

Uma serie de problemas pode ser representado por LMIs: inequacoes lineares,

inequacoes lineares quadraticas e condicoes que surgem de problemas de controle,

como Lyapunov e inequacoes matriciais, sao alguns exemplos [12]. Considere a

inequacao de Lyapunov como um exemplo simples de LMI:

ATP + PA < 0

A matriz A ∈ Rn×n e conhecida e a matriz P = P T e a variavel.

Mesmo que varios problemas de controle possam ser expressos na forma de LMIs,

alguns desses problemas podem resultar em desigualdades matriciais nao lineares.

Existem alguns “truques” utilizados para transformar essas desigualdades nao line-

ares em formas permitidas para LMIs [29]. Alguns deles sao: mudanca de variaveis,

Procedimento-S e Complemento de Schur.

Nesse trabalho, o “truque” mais utilizado e baseado no Complemento de Schur.

Para entender melhor como o Complemento de Schur e utilizado para transformar

inequacoes em LMIs, considere a seguinte LMI e o conjunto de inequacoes:

Q(x) S(x)

S(x)T R(x)

> 0 (5.3)

R(x) > 0, Q(x)− S(x)R(x)−1ST > 0 (5.4)

Pelo Complemento de Schur, e facil perceber que o conjunto de inequacoes (5.4)

pode ser representado pela LMI (5.3).

Outro exemplo da utilizacao do Complemento de Schur para reescrever uma ine-

quacao como uma LMI e a equacao algebrica de Riccati:

56

ATP + PA+ PBR−1BTP +Q < 0 (5.5)

onde A, B, Q e R sao matrizes conhecidas de tamanho apropriado, sendo Q e

R matrizes positivas definidas, e P = P T e a variavel. A inequacao (5.5) pode ser

expressa pela seguinte LMI:

−ATP − PA−Q PB

BTP R

> 0 (5.6)

Essa transformacao e feita utilizando o conceito do Complemento de Schur. Cha-

mando −ATP − PA − Q de A, PB de B e R de C, e possıvel utilizar o resultado

obtido no Capıtulo 2, Definicao 2.1. Para que a matriz da LMI (5.6) seja maior que

0 e necessario que:

C > 0, A− BC−1BT > 0

Expandindo o termo A− BC−1BT > 0:

−ATP − PA−Q− PBR−1BTP > 0

Multiplicando por −1:

ATP + PA+Q+ PBR−1BTP < 0 (5.7)

A inequacao (5.7) e igual a (5.5) e prova que e possıvel expressar (5.5) pela LMI

(5.6). Alem disso, ao representar a inequacao (5.5) como uma LMI, fica claro que a

inequacao e convexa, o que nao e obvio a primeira vista.

Existem tres problemas mais comuns envolvendo LMIs, sao eles: o problema da

admissibilidade, o problema do autovalor e o problema do autovalor generalizado.

57

O problema da admissibilidade corresponde a, dada uma LMI F (x) > 0, encon-

trar xfeas tal que que F (xfeas) > 0 ou determinar que a LMI nao possui solucao

admissıvel. Esse problema e um problema de admissibilidade convexa. Um exemplo

de um problema de admissibilidade e o problema de estabilidade de Lyapunov para

varias matrizes. Dadas as matrizes Ai ∈ Rn×n, i = 1, . . . , L, e necessario encontrar

um matriz P que satisfaca a LMI:

P > 0, ATi P + PAi < 0, i = 1, . . . , L

Ou determinar que nao existe nenhuma matriz P que satisfaca essa LMI.

O problema do autovalor tem como objetivo minimizar o autovalor maximo de

uma matriz que depende diretamente de uma variavel, sujeito a uma restricao dada

por uma LMI (ou determinar que essa restricao nao possui solucao). Um exemplo

e:

minizar λ

sujeito a λI − A(x) > 0, B(x) > 0

Onde A e B sao matrizes simetricas que dependem diretamente da otimizacao da

variavel x. Esse tipo de problema e um problema de otimizacao convexa.

Esse tipo de problema tambem pode aparecer na forma equivalente de mini-

mizacao de uma funcao linear sujeita a uma LMI, por exemplo:

minizar cTx

sujeito a F (x) > 0

Onde F e uma funcao que depende diretamente de x. No caso especial onde

as matrizes Fi sao todas diagonais o problema e reduzido a um problema de pro-

gramacao linear: minimizar a funcao linear cTx sujeita a um conjunto de inequacoes

lineares em x.

58

Para ficar mais claro o que e um problema do autovalor, considere o problema um

pouco mais complexo:

minizar γ

sujeito a

−ATP − PA− CTC PB

BTP γI

> 0, P > 0

As matrizes A ∈ Rn×n, B ∈ Rn×p e C ∈ Rm×n sao conhecidas e P e γ sao as

variaveis a serem otimizadas.

Por fim, o problema do autovalor generalizado tem como objetivo minimizar o

maximo autovalor generalizado de um par de matrizes que dependem diretamente

de uma variavel, sujeito a restricao dada por uma LMI. Esse problema tem a seguinte

forma geral:

minizar λ

sujeito a λB(x)− A(x) > 0, B(x) > 0, C(x) > 0

Onde A,B e C sao matrizes simetricas que sao funcoes de x. Esse problema pode

ser expresso como:

minizar λmax(A(x), B(x))

sujeito a B(x) > 0, C(x) > 0

Onde λmax(A(x), B(x)) denota o maior autovalor generalizado de λB(x)−A(x) >

0 com B(x) > 0. Esse tipo de problema e um problema de otimizacao quase convexo

uma vez que a restricao e convexa, porem o objetivo, λmax(A(x), B(x)), e quase

convexo.

Um exemplo de um problema do autovalor generalizado e:

59

minizar α

sujeito a − ATP − PA− 2αP > 0, P > 0

Onde a matriz A e conhecida e as variaveis a serem otimizadas sao a matriz

simetrica P e o escalar α.

Esses tres tipos de problemas podem ser resolvidos em tempo polinomial e po-

dem ser resolvidos na pratica de forma eficiente. Resolver esses problemas significa

determinar se o problema possui ou nao solucao admissıvel e, caso possua, calcular

um ponto que respeite o objetivo a ser atingido dentro de uma acuracia pre definida

[12].

5.2 Estabilidade de TDSs

O conceito de estabilidade foi definido no Capıtulo 2 para sistemas que nao pos-

suem atraso e apesar de nao ser muito diferente para sistemas com atraso, e impor-

tante definir o conceito para TDSs.

Considere o seguinte TDS:

x = f(t, xt), t ≥ t0

x(t0 + s) = ϕ(s), s ∈ [−h, 0] (5.8)

onde h > 0 representa o atraso e ϕ(s) e a funcao que representa a condicao inicial.

O estado do sistema, denotado por xt, e definido por:

xt(θ) = x(t+ θ), θ ∈ [−h, 0]

Assume-se que o sistema (5.8) admite a solucao x(t) = 0, ou seja, f(t, 0) = 0, que

e normalmente referida como solucao trivial.

60

Definicao 5.1 Considere φ, entao a norma uniforme de φ e definida como

||φ||C = maxs∈[a,b]

|φ(s)| (5.9)

Definicao 5.2 Considere o sistema com atraso (5.8). A solucao trivial e dita

� estavel no sentido de Lyapunov se para qualquer t0 ≥ 0 e qualquer ε > 0,

existe δ = δ(t0, ε) > 0 tal que

‖xt0‖C ≤ δ ⇒ |x(t)| ≤ ε (5.10)

para todo t ≥ t0.

� atrativa se para qualquer t0 ≥ 0 e qualquer ε > 0, existe δ = δ(t0, ε) > 0 com

a propriedade

‖xt0‖C ≤ δa ⇒ limt→∞|x(t)| = 0 (5.11)

� assintoticamente estavel se e estavel e atrativa.

� uniformemente estavel se e estavel e δ = δ(t0, ε) nao depende de t0.

� exponencialmente estavel se existe δ, α > 0 e β ≥ 1 tal que

‖xt0‖C ≤ δ ⇒ |x(t)| ≤ βe−αt |x0| (5.12)

para todo t ≥ 0.

� instavel se nao e estavel no sentido de Lyapunov

Assim como em sistemas sem atraso, um metodo eficiente para analise da estabi-

lidade de TDSs e o metodo direto de Lyapunov. Os dois metodos mais comuns para

TDSs sao: Lyapunov-Krasovskii e Lyapunov-Razumikhin. Na literatura, boa parte

das estrategias de controle por modos deslizantes propostas para controlar TDSs

fazem uso da teoria de Lyapunov-Krasovskii, como, por exemplo, nos seguintes tra-

balhos [13, 31, 32, 5, 4, 7]. Dessa forma, esse trabalho ira se aprofundar apenas

no metodo de Lyapunov-Krasovskii. Mais detalhes sobre o metodo de Lyapunov-

Razumikhin podem ser encontrados em [2].

61

5.3 Lyapunov-Krasovskii

Considere a seguinte RDE:

x(t) = f(t, xt), t ≥ t0 (5.13)

Assuma que (5.13) possua a solucao trivial x(t) = 0 e que possua a condicao

inicial x(θ) = ϕ(θ), θ ∈ [−h, 0].

Considerando V (x) um funcional contınuo e possıvel definir o seguinte teorema:

Teorema 5.1 Supondo f(t, xt) e que u(s), v(s), w(s) sao funcoes contınuas e nao

decrescentes, ou seja, u(s) e v(s) sao positivas para s > 0, e u(0) = v(0) = 0. A

solucao trivial de (5.13) e estavel se existe um funcional contınuo V , que e positivo

definido

u(|ϕ(0)|) ≤ V (t, ϕ) ≤ v(||ϕ||C) (5.14)

tal que sua derivada ao longo da trajetoria (5.13) e nao positiva

V (t, ϕ) ≤ −w(|ϕ(0)|) (5.15)

Se w(s) > 0 para s > 0, entao a solucao trivial e assintoticamente estavel. Se, alem

disso, lims→∞ u(s) =∞, a solucao trivial e globalmente assintoticamente estavel.

Prova: ver [2].

5.3.1 Condicoes para estabilidade de TDSs

Como foi citado no capıtulo anterior, ao realizar a analise de sistemas com atraso

utilizando o metodo direto de Lyapunov, e possıvel obter condicoes que dependem

do atraso ou condicoes que nao dependem do atraso. Naturalmente isso significa

que a estabilidade do sistema pode depender ou nao do atraso [33, 1]. Apesar de

representarem de forma um pouco mais realista os sistemas de controle praticos, as

condicoes dependentes do atraso possuem formulacao matematica mais complexa e,

como fogem do escopo desse trabalho, nao serao abordadas. Informacoes detalhadas

dessas condicoes podem ser encontradas em [33, 2].

62

Aqui sera explorado apenas o caso de condicoes independentes. Para isso, consi-

dere a seguinte RDE linear:

x = Ax(t) + A1x(t− τ(t)), t ≥ t0 (5.16)

onde x(t) ∈ Rn, com um atraso variante no tempo τ(t) ∈ [0, h]. A e A1 sao

matrizes constantes n× n.

Para a analise da estabilidade de (5.16) com atraso constante τ = h, uma forma

geral para o funcional de Lyapunov-Krasovskii e:

V (xt) = xT (t)Px(t) + 2xT (t)

∫ 0

−hQ(ξ)x(t+ ξ)dξ

+

∫ 0

−h

∫ 0

−hxT (t+ s)R(s, ξ)x(t+ ξ)dsdξ (5.17)

Esse funcional de Lyapunov-Krasovskii leva a problemas complicados e e comu-

mente substituıdo por uma versao mais simples:

V (t, xt) = xTPx+

∫ t

t−τ(t)

xT (s)Qx(s)ds (5.18)

P e Q sao matrizes positivas definidas n×n. Em (5.18) V depende do tempo por

conta do termo τ(t). No caso onde o atraso e constante τ = h, o funcional (5.18) nao

dependera mais do tempo. Para o caso onde o atraso e de fato variante no tempo,

assume-se que τ ≤ d < 1, que representa os atrasos que variam lentamente com o

tempo. O funcional acima satisfaz a condicao (5.14) do Teorema 5.1 e derivando V

ao longo das trajetorias de (5.16), obtem-se:

V (t, xt) = xT (t)Px(t) + xT (t)Px(t) + xT (t)Qx(t)− (1− τ)xT (t− τ)Qx(t− τ)

Substituindo x(t) da equacao (5.16):

63

V (t, xt) ≤ xT (t)(ATP + PA+Q)x(t) + xT (t)PA1x(t− τ)

+ xT (t− τ)AT1 Px(t)− (1− d)xT (t− τ)Qx(t− τ)

V (t, xt) =[xT (t) xT (t− τ)

]W

x(t)

x(t− τ)

≤ α |x(t)|2

para algum α > 0 se

W =

ATP + PA+Q PA1

AT1 P −(1− d)Q

< 0 (5.19)

A LMI (5.19) nao depende do atraso h e e dessa forma independente do atraso,

apesar de depender da derivada do atraso. Pelo Teorema 5.1, a viabilidade da LMI

(5.19) e uma condicao suficiente para a estabilidade assintotica uniforme de sistemas

com atrasos que variam lentamente no tempo. Esse resultado pode ser resumido da

seguinte maneira:

� O sistema (5.16) e assintoticamente uniformemente estavel para qualquer atraso

τ(t) com τ ≤ d < 1 se existem as matrizes positivas definidas P e Q tal que a

LMI (5.19) possui solucao.

64

Capıtulo 6

SMC aplicado a Sistemas com

Atraso

Esse capıtulo tem como objetivo apresentar a tecnica de controle desenvolvida

para controlar sistemas com atraso, baseada no artigo [4]. Essa tecnica utiliza o

conceito de controle por modos deslizantes (SMC), mais especificamente o controle

por modos deslizantes integral (ISMC). Sao controlados sistemas incertos com atra-

sos na sua propria dinamica e na entrada, incertezas parametricas descasadas e

perturbacoes externas. A estabilidade global do sistema em malha fechada e garan-

tida utilizando a teoria de estabilidade de Lyapunov e o conceito de LMIs. Alem

disso, e atingida uma norma H∞ limitada da atenuacao da perturbacao existente no

sistema. O metodo proposto tem como principais vantagens:

� a ordem da equacao do movimento durante o deslizamento e igual a ordem do

sistema original;

� a robustez do sistema e garantida durante toda a reposta do sistema, desde o

tempo inicial;

� a estabilidade assintotica e garantida sem a necessidade do uso de preditores

de estado.

Uma desvantagem que esse metodo possui e a necessidade de se saber perfeita-

mente a informacao de algumas matrizes do sistema, o que nem sempre e facil de se

obter em sistemas praticos.

65

Notacao: Durante esse capıtulo, x(t) sera chamado de estado para seguir a

convencao encontrada na literatura, porem a definicao formal de estado para um

sistema com atraso e a encontrada no Capıtulo 4. As entradas indicadas por ∗

representam entradas simetricas na matriz.

6.1 Formulacao do Problema

Considere o seguinte TDS incerto:

x(t) = (A+ ∆A(t))x(t) + Adx(t− h) +Bu(t) +Bdu(t− h) +B1w(t)

y(t) = Cx(t)

x(t) = 0, u(t) = 0 t < 0; x(0) = x0, u(0) = u0 (6.1)

Em (6.1), x(t) ∈ Rn e o estado, u(t) ∈ Rm e a entrada de controle, w(t) ∈ Rl

e a perturbacao externa, que possui ‖w(t)‖ ≤ δw, y(t) ∈ Rp e a saıda do sinal

controlado, A,Ad, B e Bd sao matrizes conhecidas de dimensoes apropriadas e h > 0

e o atraso no tempo, constante e conhecido. A incerteza parametrica ∆A(t) nao e

conhecida e e variante com o tempo, alem disso, assume-se que ela e limitada em

norma e possui a seguinte forma:

∆A(t) = D1F (t)E1 (6.2)

Onde D1 e E1 sao matrizes conhecidas de dimensoes apropriadas, que representa

a estrutura da incerteza, e F (t) e uma matriz desconhecida satisfazendo:

F T (t)F (t) ≤ I (6.3)

O objetivo, entao, e desenvolver um controlador por modo deslizante robusto que

estabilize a classe de sistemas incertos com atrasos na sua propria dinamica e na

entrada. Alem disso, o controlador deve assegurar que os efeitos da perturbacao

na saıda do sistema sejam atenuados. A norma da saıda, passa a ser limitada pela

norma da perturbacao conforme a definicao a seguir:

66

Definicao 6.1 Sujeita a condicoes iniciais nulas, x(t) = 0, t < 0, a saıda do sinal

controlado y(t) e dita ser ‖Tyw‖ ≤ γ, γ > 0, caso satisfaca ‖y(t)‖2 < γ ‖w(t)‖2 para

qualquer perturbacao nao nula w(t).

6.2 Projeto da superfıcie de deslizamento

O primeiro passo para realizar o projeto de um controlador baseado no SMC e

especificar a superfıcie de deslizamento. Nesse trabalho, sera utilizada uma superfıcie

de deslizamento integral, baseada nos conceitos citados no Capıtulo 3:

s(t) = Gx(t) + z(t)

s(t) = Gx(t) +Gx(0)−G∫ t

0

[(A+BK)x(τ) + Adx(t− τ) +Bdu(t− τ)] dτ︸︷︷︸z(t)

(6.4)

Onde a matriz G ∈ Rm×n e escolhida de forma que GB seja nao singular e

K ∈ Rm×n e projetado tal que o sistema (6.1) seja assintoticamente estavel durante

o deslizamento.

A seguir, sao derivadas as condicoes para avaliar a estabilidade e robustez do TDS

incerto (6.1) restrito a superfıcie de deslizamento s(t) = 0. Essas condicoes estao

sujeitas a existencia de matrizes positivas definidas apropriadas.

Teorema 6.1 O TDS incerto (6.1) com w(t) = 0 e assintoticamente estavel no

modo deslizante se a superfıcie de deslizamento integral (6.4) e usada, e existem

matrizes positivas definidas R1 ∈ Rn×n, R2 ∈ Rm×m e P ∈ Rn×n para qualquer

matriz incerta F (t) admissıvel tal que a seguinte inequacao e satisfeita

Ξ = Π1 + Π2R−11 ΠT

2 + PBdR−12 BT

d P < 0 (6.5)

onde

67

Π1 = P (A+DaF (t)Ea +BK) + (A+DaF (t)Ea +BK)TP +R1 +KTR2K

Π2 = P (Ad +DdF (t− h)Ed)

Da = [I −B(GB)−1G]D1

Dd = −Bd(GB)−1GD1

Ea = Ed = E1

Prova: ver [4].

Teorema 6.2 Considere o TDS incerto (6.1) com superfıcie de deslizamento inte-

gral definida pela funcao (6.4). Se existe uma constante γ > 0 e matrizes positivas

definidas R1 ∈ Rn×n, R2 ∈ Rm×m e P ∈ Rn×n tais que para qualquer matriz incerta

F (t) admissıvel a seguinte inequacao e satisfeita

T = Π1 + Π2R−11 ΠT

2 + PBdR−12 BT

d P + CTC + γ−2PB1BT1 P < 0 (6.6)

onde Π1 e Π2 sao definidas em (6.5). Entao, durante o deslizamento, o sistema

(6.1) e assintoticamente estavel e ‖Tyw‖ ≤ γ.

Prova: ver [4].

O proximo teorema visa formular o Teorema 6.2 na forma de LMI, alem de definir

o valor do ganho K.

Teorema 6.3 O TDS incerto (6.1) com superfıcie de deslizamento integral dada por

(6.4) e assintoticamente estavel durante o deslizamento e ‖Tyw‖ ≤ γ se existe uma

constante γ > 0, uma constante positiva ε > 0, uma matriz W ∈ Rm×n e matrizes

positivas definidas M1 ∈ Rn×n, M2 ∈ Rm×m e X ∈ Rn×n tais que a seguinte LMI e

satisfeita

68

Λ AdM1 BdM2 X W T XETa 0 XCT

∗ −M1 0 0 0 0 M1ETd 0

∗ ∗ −M2 0 0 0 0 0

∗ ∗ ∗ −M1 0 0 0 0

∗ ∗ ∗ ∗ −M2 0 0 0

∗ ∗ ∗ ∗ ∗ −εI 0 0

∗ ∗ ∗ ∗ ∗ ∗ −εI 0

∗ ∗ ∗ ∗ ∗ ∗ ∗ −I

< 0 (6.7)

onde Λ = AX+XAT +BW +W TBT +εDaDTa +εDdD

Td +γ−2B1B

T1 . Alem disso,

a matriz de ganho K e dada por

K = WX−1 (6.8)

Prova: ver [4].

E importante dizer que nesse trabalho sera considerado apenas os casos onde o

atraso e constante, porem a estrategia escolhida tambem pode ser expandida para

lidar com sistemas que possuem atraso variavel, desde que h(t) ≤ ρh < 1 [4].

6.3 Projeto do controlador

O proximo passo apos o desenvolvimento da superfıcie de deslizamento e o de-

senvolvimento de uma lei de controle apropriada que satisfaca a condicao de al-

cancabilidade-η, ss ≤ −η|s|. Essa condicao garante que que a lei de controle levara

o sistema ate a superfıcie de deslizamento e o mantem nela uma vez que foi al-

cancada. A escolha da lei de controle se baseia na lei apresentada para o ISMC no

Capıtulo 3:

u(t) = uo(t) + un(t) (6.9)

69

Nesse caso, o ganho de feedback, uo(t), e usado para confirmar a performance do

SMC e e escolhido como uo(t) = Kx(t), com a matriz K dada por (6.8). O termo

nao linear, un(t), e utilizado para induzir o modo deslizante e vencer o efeito de

qualquer perturbacao externa ou variacao de parametro do sistema (6.1), possui a

seguinte forma:

un(t) = −(GB)−1ρ(t, x)s(t)

‖s(t)‖(6.10)

Dessa forma, a equacao (6.9) pode ser reescrita como:

u(t) = Kx(t)− (GB)−1ρ(t, x)s(t)

‖s(t)‖(6.11)

Como foi indicado no Capıtulo 3, uma boa escolha para a matriz G e:

G = B+ =(BTB

)−1BT (6.12)

Essa escolha de G com a pseudo inversa de B traz como principal vantagem a nao

amplificacao de incertezas descasadas. Alem disso, ela leva a seguinte propriedade:

GB =(BTB

)−1BT︸︷︷︸

G

B = Im

O termo ρ(t, x) e encontrado provando que o controlador (6.11) satisfaz a condicao

de alcancabilidade-η. Assim:

s(t) = Gx(t)−G(A+BK)x(t)−GAdx(t− h)−GBdu(t− h)

= G∆A(t)x(t) +GBu(t) +GB1w(t)−GBKx(t) (6.13)

Para encontrar a condicao de alcancabilidade-η e necessario fazer sT (t)s(t), por-

tanto, multiplicando (6.13) por sT (t), utilizando a equacao (6.11) para u(t) e os

fatos GB = I e sT (t)s(t) = ‖s(t)‖2, obtem-se:

70

sT (t)s(t) = sT (t)(G∆A(t)x(t) +GBu(t) +GB1w(t)−GBKx(t))

= sT (t)G∆A(t)x(t)− ρ(t, x) ‖s(t)‖2 + sT (t)GB1w(t)

≤ ‖s(t)‖ (−ρ(t, x) + ‖G∆A(t)x(t)‖+ ‖GB1w(t)‖) (6.14)

O valor da modulacao ρ(t, x) deve ser maior que qualquer perturbacao ou incerteza

do sistema, portanto, ρ(t, x) deve satisfazer:

ρ(t, x) ≥ ‖G‖ ‖D1‖ ‖E1‖ ‖x(t)‖+ ‖GB1‖ δw + η (6.15)

Para obter (6.15) foram utilizadas as equacoes (6.2) e (6.3) e o fato de que ‖w(t)‖ ≤

δw. Dessa forma, com essa escolha para ρ(t, x) e possıvel escrever (6.14) como:

sT (t)s(t) ≤ −η ‖s(t)‖ (6.16)

Onde η > 0 e um parametro escolhido durante o projeto. Com o resultado (6.16),

prova-se que a condicao de alcancabilidade-η e satisfeita e o termo de controle e

dado por (6.11) com ρ(t, x):

ρ(t, x) = ‖G‖ ‖D1‖ ‖E1‖ ‖x(t)‖+ ‖GB1‖ δw + η (6.17)

Com a escolha da lei de controle (6.11) e com as matrizes satisfazendo a LMI (6.7)

e garantido que o TDS incerto (6.1) e assintoticamente estavel.

Por fim, um ultimo ajuste deve ser feito na lei de controle para evitar o efeito do

chattering causado pelo termo s(t)‖s(t)‖ . Utilizando o uso do conceito de boundary layer

citado no Capıtulo 3, substitui-se s(t)‖s(t)‖ por uma funcao de saturacao. Dessa forma,

a lei de controle (6.11) e reescrita como:

u(t) = Kx(t)− (GB)−1ρ(t, x) sat

(s(t)

δ

)(6.18)

Onde δ e a medida da espessura da camada de fronteira (boundary layer).

71

6.4 Exemplo Ilustrativo

Essa secao visa ilustrar e mostrar a viabilidade da estrategia desenvolvida por

meio de um exemplo numerico. Considere um TDS incerto descrito por (6.1) com:

A =

−1 0

0.2 0.3

, Ad =

0.01 −0.04

0.02 0

, B =

2

1

,

Bd =

1

0

, h = 0.8

Para ilustrar a utilizacao do esquema proposto, sao escolhidas tambem as matrizes

da incerteza parametrica, da perturbacao externa e do sinal controlado na saıda:

D1 =

0.1

0.1

, F (t) = sen(t), E1 =[0 1

], B1 =

0

0.1

,

w(t) = sen(t)e−t, C =[1 0

]De acordo com (6.12), G e escolhido de forma que GB = I e escolhe-se γ = 0.5.

Com esses dados, basta resolver a LMI (6.7). A referencia [4] utiliza o LMI Toolbox

para encontrar a solucao da LMI. Por dificuldades de implementacao encontradas

com esse Toolbox, sera utilizada a ferramenta Yalmip, uma vez que a definicao e

resolucao da LMI e mais intuitiva por meio dela e os resultados obtidos nao afetam

o desempenho final do sistema. As solucoes obtidas para ε, W , M1, M2 e X sao:

1 epsilon = 1.4484

2

3

4 M1 = 1.4184 -0.0660

5 -0.0660 0.7131

6

7

8 M2 = 0.5100

9

10

72

11 W = -0.1719 -0.1469

12

13

14 X = 0.6856 0.0112

15 0.0112 0.0642

16

17 % K = WXˆ-1

18 K = -0.2139 -2.2499

Com os valores obtidos, a lei de controle (6.18) fica:

u(t) =[−0.2139 −2.2499

]x(t)− (‖G‖ ‖D1‖ ‖E1‖ ‖x(t)‖+ ‖GB1‖+ 1) sat

(s(t)

0.1

)Onde foram escolhidos η = 1, δ = 0.1 e δw = 1. Para δw foi escolhido esse valor,

pois essa modulacao precisa vencer o valor da perturbacao externa w(t), que possui

valor maximo igual a 1. Para δ, quanto mais proximo de 0, mais perto do termo

s(t)‖s(t)‖ fica a aproximacao feita pela saturacao, portanto 0.1 e um valor razoavel.

As figuras a seguir ilustram o resultado da simulacao do sistema, com uma

condicao inicial x(0) =[−1 2

]T. A figura 6.1 mostra as trajetorias do sistema,

confirmando a estabilidade assintotica do sistema em malha fechada. A figura 6.2

mostra a entrada de controle e pode ser visto que o fenomeno do chattering e eli-

minado. A figura 6.3 mostra a superfıcie de deslizamento e fica claro que, com as

escolhas apropriadas dos termos, a fase de aproximacao e eliminada e o sistema entra

em modo deslizante desde o primeiro instante.

73

Figura 6.1: Trajetorias do sistema do exemplo considerado.

Figura 6.2: Sinal de controle do exemplo considerado.

Figura 6.3: Superfıcie de deslizamento do exemplo considerado.

74

Em comparacao com o artigo [4], as mudancas feitas no projeto da superfıcie de

deslizamento e na matriz G fazem com que o sistema obtenha o comportamento

esperado, uma vez que a tecnica se baseia no ISMC. Dessa forma, ao inves do

sistema possuir uma fase de aproximacao como e visto em [4], a fase de aproximacao

e eliminada e o sistema desliza desde o inıcio da resposta em malha fechada.

Para ilustrar isso foi feita a simulacao novamente, porem trocando apenas o valor

de G e a forma que superfıcie de deslizamento foi projetada, seguindo o proposto

em [4]. Como esperado, a superfıcie de deslizamento passa a possuir a fase de

aproximacao.

Figura 6.4: Superfıcie de deslizamento projetada como em [4].

Dessa forma, fica claro que as mudancas realizadas no projeto melhoram o de-

sempenho do sistema, fazendo com que ele entre em deslizamento durante toda a

resposta em malha fechada.

Diante dos resultados apresentados, fica claro que estrategia de controle proposta

possui boa performance e robustez contra atrasos na sua propria dinamica e na

entrada, incertezas parametricas descasadas e perturbacoes externas.

75

Capıtulo 7

Conclusao

Esse trabalho apresentou uma tecnica de controle robusto capaz de controlar

sistemas incertos com atraso. Para isso, primeiramente foi apresentado um estudo

sobre os conceitos matematicos mais importantes que permeiam todo o texto.

A partir desse ponto, foi apresentado um estudo sobre o controle por modos desli-

zantes, verificando suas principais propriedades, vantagens e dificuldades de imple-

mentacao. Dentro desse contexto, foi dada enfase ao estudo do controle por modos

deslizantes integral (Integral Sliding Mode Control - ISMC ), devido as suas vanta-

gens apresentadas em comparacao com controle por modos deslizantes convencional.

Duas de suas vantagens mais importantes sao a eliminacao da fase de aproximacao e

a capacidade de lidar com incertezas descasadas, desde que sejam seguidas algumas

regras para escolha dos parametros do sistema.

O trabalho entao apresentou com mais detalhes a classe de sistemas considerada.

O estudo sobre sistemas com atraso mostrou a dificuldade matematica que a in-

clusao do atraso traz para a analise do sistema. Dessa forma, foi delimitado que os

sistemas a serem controlados seriam sistemas com atrasos discretos, que possuem

sua formulacao matematica na forma de equacoes diferenciais retardadas. A seguir,

foi apresentado o conceito de desigualdade matriciais lineares (Linear Matrix Ine-

qualities - LMI ) e estabilidade para sistemas com atraso. Foi demonstrado que,

utilizando a Teoria de Lyapunov, a estabilidade de um TDS pode ser analisada por

meio de uma LMI.

76

Tendo como motivacao o fato de que muitos sistemas praticos sao incertos, foi

proposto um esquema de controle baseado no ISMC para controlar sistemas incer-

tos e que possuem atraso. Foi considerado o caso mais geral onde o sistema pode

possuir atraso na entrada e no estado. Alem disso, como a lei de controle utili-

zou os conceitos do ISMC, a estrategia desenvolvida foi capaz de nao amplificar os

efeitos das incertezas descasadas. Esta estrategia possui desempenho satisfatorio,

garantindo a estabilidade assintotica do sistema em malha fechada. As condicoes

necessarias para estabilidade do sistema foram encontradas por meio de uma LMI.

O trabalho tem como contribuicoes o uso de LMIs para analise da estabilidade do

sistema e o uso do ISMC para o projeto do controlador. Como trabalhos futuros,

pode-se estudar se e possıvel de fato utilizar o esquema proposto para sistemas com

atraso variavel. Alem disso, pode-se estudar a possibilidade do desenvolvimento de

alguma algoritmo de controle para sistemas discretos com atraso. Uma outra possi-

bilidade e estudar o controle de sistemas a dados amostrados como sendo equivalente

a um sistema contınuo com atraso variavel.

77

Referencias Bibliograficas

[1] FRIDMAN, E., “Tutorial on Lyapunov-based methods for time-delay systems”,

European Journal of Control, v. 20, n. 6, pp. 271 – 283, 2014.

[2] FRIDMAN, E., Introduction to Time-Delay Systems: Analysis and Control,

Systems & Control: Foundations & Applications. Springer International Pu-

blishing, 2014.

[3] SLOTINE, J., LI, W., Applied Nonlinear Control. Prentice Hall, 1991.

[4] PAI, M.-C., “Sliding Mode Control of Vibration in Uncertain Time-delay Sys-

tems”, Journal of Vibration and Control, v. 16, pp. 2131–2145, 2010.

[5] ZHANG, X., “Integral sliding mode control for uncertain systems with input

delay based on singular perturbation approach”. In: Proceeding of the 11th

World Congress on Intelligent Control and Automation, pp. 4657–4662, 2014.

[6] RICHARD, J.-P., GOUAISBAUT, F., PERRUQUETTI, W., “Sliding Mode

Control in the Presence of Delay”, Kybernetika, v. 3, pp. 277–294, 2001.

[7] PAI, M.-C., “Chaotic sliding mode controllers for uncertain time-delay chao-

tic systems with input nonlinearity”, Applied Mathematics and Computation,

v. 271, pp. 757 – 767, 2015.

[8] HUNG, J. Y., GAO, W., HUNG, J. C., “Variable Structure Control: A Survey”,

IEEE Transactions on Industrial Eletronics, v. 40, pp. 2–22, 1993.

[9] NUNES, E. V. L., Controle por modos deslizantes de ordem superior com es-

tabilidade global. M.Sc. dissertation, Universidade Federal do Rio de Janeiro,

Maio 2004.

78

[10] UTKIN, V. I., “Variable structure systems with sliding modes”, IEEE Tran-

sactions on Automatic Control, v. 22, pp. 212–222, 1977.

[11] UTKIN, V. I., Sliding Modes and Their Application in Variable Structure Sys-

tems. MIR, 1978.

[12] BOYD, S., EL GHAOUI, L., FERON, E., et al., Linear Matrix Inequalities in

System and Control Theory. Society for Industrial and Applied Mathematics,

1994.

[13] FRIDMAN, E., HAN, X., SPURGEON, S., “A Singular Perturbation Approach

to Sliding Mode Control in the Presence of Input Delay”, IFAC Proceedings

Volumes, v. 43, pp. 1272 – 1277, 2010.

[14] STRANG, G., Linear algebra and its applications. 4 ed. Thomson, Brooks/Cole,

2006.

[15] GALLIER, J., “http://www.cis.upenn.edu/∼jean/schur-comp.pdf”, 2010,

(Acesso em 21 Junho 2018).

[16] FRIDMAN, E., “New Lyapunov-Krasovskii functionals for stability of linear

retarded and neutral type systems”, Systems & Control Letters, v. 43, n. 4,

pp. 309 – 319, 2001.

[17] EDWARDS, C., SPURGEON, S., Sliding mode control: theory and applications,

Series in Systems and Control. Taylor & Francis, 1988.

[18] SHTESSEL, Y., EDWARDS, C., FRIDMAN, L., et al., Sliding Mode Control

and Observation. Springer Science New York, 2014.

[19] LEE, H., UTKIN, V. I., “Chattering suppression methods in sliding mode con-

trol systems”, Annual Reviews in Control, v. 31, pp. 179 – 188, 2007.

[20] FILIPPOV, A. F., “Differential Equations with Discontinuous Right-Hand

Side”, Translations. Series 2. American Mathematical Society., v. 42, n. 2,

pp. 199 – 231, 1964.

[21] FILIPPOV, A. F., Differential Equations with Discontinuous Righthand Side.

Kluwer Academic Publishers, 1988.

79

[22] HAMAYUN, M. T., EDWARDS, C., ALWI, H., Fault Tolerant Control Schemes

Using Integral Sliding Modes, Studies in Systems, Decision and Control 61. 1

ed. Springer International Publishing, 2016.

[23] UTKIN, V. I., “Sliding mode control design principles and applications to elec-

tric drives”, IEEE Transactions on Industrial Electronics, v. 40, pp. 23–36,

1993.

[24] UTKIN, V. I., LEE, H., “Chattering Problem in Sliding Mode Control Sys-

tems”. In: International Workshop on Variable Structure Systems, 2006.

VSS’06., pp. 346–350, 2006.

[25] RICHARD, J.-P., “Time-delay systems: an overview of some recent advances

and open problems”, Automatica, v. 39, n. 10, pp. 1667 – 1694, 2003.

[26] MIRKIN, L., “Introduction to Time-Delay Systems”, 2012.

[27] SEURET, A., GOUAISBAUT, F., BAUDOUIN, L., D1.1 -Overview of Lyapu-

nov methods for time-delay systems, Research report, LAAS-CNRS, 2016.

[28] BRIAT, C., Linear Parameter-Varying and Time-Delay Systems: Analysis, Ob-

servation, Filtering & Control, chapter Introduction to Time-Delay Systems,

Berlin, Heidelberg, Springer Berlin Heidelberg, pp. 123–164, 2015.

[29] ZHANG, J., SWAIN, A. K., NGUANG, S., Robust Observer-Based Fault Di-

agnosis for Nonlinear Systems Using MATLAB®. Springer International Pu-

blishing, 2016.

[30] GAHINET, P., NEMIROVSKIAND, A., LAUB, A., et al., LMI control toolbox

user’s guide. The MathWorks, Inc., 1995.

[31] HAN, X., FRIDMAN, E., SPURGEON, S., “Sliding mode control in the pre-

sence of input delay: A singular perturbation approach”, Automatica, v. 48,

n. 8, pp. 1904 – 1912, 2012.

[32] XIA, Y., YANG, H., FU, M., et al., “Sliding Mode Control for Linear Systems

with Time-Varying Input and State Delays”, Circuits, Systems, and Signal

Processing, v. 30, n. 3, pp. 629 – 641, 2011.

80

[33] BRIAT, C., Linear Parameter-Varying and Time-Delay Systems: Analysis, Ob-

servation, Filtering & Control, chapter Stability Analysis of Time-Delay Sys-

tems, Berlin, Heidelberg, Springer Berlin Heidelberg, pp. 165–242, 2015.

[34] GRANT, M. C., BOYD, S. P., The CVX Users Guide Release 2.1. CVX Rese-

arch, Inc., 2017.

[35] LOFBERG, J., “YALMIP : a toolbox for modeling and optimization in MA-

TLAB”. In: 2004 IEEE International Conference on Robotics and Automation

(IEEE Cat. No.04CH37508), pp. 284–289, 2004.

81

Apendice A

Toolboxs para resolucao de LMIs

Este trabalho faz uso do Matlab para a resolucao de LMIs. As tres ferramentas

mais comuns para resolucao de LMIs no Matlab sao: Yalmip, CVX e LMI Control

Toolbox. As duas primeiras sao mais recentes e podem ser instaladas de graca no

Matlab, a ultima e incluıda na instalacao do Matlab.

As duas ferramentas mais recentes, Yalmip e CVX, sao na verdade linguagens de

modelagem que somam-se ao Matlab para tornar possıvel a resolucao de problemas

convexos, como e o caso das LMIs [34, 35]. Ja o LMI Control Toolbox implementa

ferramentas para analise e projeto de sistemas robustos baseando-se no conceito de

LMI. Alem disso, oferece um ambiente para especificar e resolver LMIs, o LMI Lab

[30].

A resolucao de fato de alguma LMI em qualquer uma das tres ferramentas so e

capaz de ser realizada utilizando algum solver. O LMI Control Toolbox traz consigo

tres solvers diferentes que sao capazes de resolver os tres problemas mais comuns

envolvendo LMIs: o problema da admissibilidade, o problema do autovalor e o

problema do autovalor generalizado, explicados com mais detalhes no Capitulo 5 [30].

No caso das linguagens de modelagem, os solvers nao sao acoplados e exclusivos das

ferramentas e sao desenvolvidos por terceiros, sendo possıvel ambas as linguagens

possuırem solvers em comum. No caso do CVX, o solver padrao e o SDPT3, porem

a instalacao da ferramenta tambem inclui outro solver, o Sedumi [34]. A instalacao

do Yalmip nao inclui os solvers mais comuns para resolucao de LMIs, por isso faz-se

necessaria a instalacao separada deles [35].

82

Cada um desses toolboxs possuem diferencas na implementacao e resolucao de

LMIs. Mais detalhes de como definir e resolver uma LMI utilizando cada uma

dessas ferramentas sao apresentados nas secoes seguintes. Todavia, antes de entrar

em detalhes sobre cada ferramenta separadamente, e importante evidenciar uma

caracterıstica que o Yalmip e o CVX possuem em comum: ambos nao permitem o

uso de LMIs estritas. Para contornar esse problema, uma solucao encontrada que

nao afeta significativamente o resultado e fazer a seguinte mudanca:

F (x) > 0

F (x) ≥ δI

Onde I e a matriz identidade de dimensao apropriada. A ideia e escolher um δ

pequeno o suficiente que permita que a ferramenta resolva a LMI, mas que nao afete

tanto o resultado final obtido.

Dessa forma, o Yalmip e o CVX possuem uma desvantagem em relacao ao LMI

Control Toolbox, que e capaz de implementar LMIs estritas. Porem, como sera visto

adiante, outras vantagens como facilidade de implementacao e a presenca de solvers

mais recentes tornam interessante o uso das linguagens de modelagem no lugar do

toolbox incluso no Matlab.

As proximas secoes tem como objetivo mostrar como especificar e resolver um

sistema de LMIs, alem de comparar os toolboxs. As referencias [35, 34, 30] foram

utilizadas como base para resolucao de problemas envolvendo LMIs em cada uma

das ferramentas e possuem mais detalhes sobre os toolboxs.

A.1 LMI Control Toolbox

O primeiro passo para resolucao de LMIs utilizando o LMI Control Toolbox e a

inicializacao da descricao do sistema de LMIs. Isso e feito utilizando o comando

setlmis([ ]).

83

Feito isso, e necessario definir as variaveis desconhecidas. Estas variaveis sao ca-

racterizadas pela sua estrutura. O comando responsavel pela definicao das variaveis

possui a seguinte estrutura: lmivar(tipo,estrutura). A definicao do argumento

estrutura depende da definicao anterior do argumento tipo, que pode ter tres valores:

� tipo = 1: estrutura simetrica em blocos diagonais. Isso corresponde a

variaveis com a seguinte forma:D1 0 . . . 0

0 D2. . .

......

. . . . . . 0

0 . . . 0 Dr

Cada bloco diagonal Dj e uma matriz quadrada, que pode ser uma matriz

nula, uma matriz simetrica completa ou uma matriz escalar. A estrutura para

esse tipo e um vetor que contem todos os blocos da matriz. Cada elemento

do vetor representa um bloco e possui dois valores: o tamanho do bloco e

a natureza do bloco (1 para um bloco simetrico completo, 0 para um bloco

escalar e -1 para um bloco nulo).

O tipo = 1 engloba as variaveis que sao escalares (1 bloco escalar de tamanho

1). Como exemplo de variaveis desse tipo, tem-se:

1 X = lmivar(1,[2 0,2 1]);

2 Y = lmivar(1,[5 1]);

3 e = lmivar(1,[1 0]);

No exemplo X possui 2 blocos diagonais, o primeiro bloco possui tamanho

2 e e escalar e o segundo bloco tambem possui tamanho 2, mas e um bloco

completo. A variavel Y possui apenas 1 bloco, sendo uma matriz simetrica

completa de dimensao igual a 5. A variavel e representa um escalar.

� tipo = 2: estrutura retangular. Corresponde a uma matriz retangular n×m,

tendo como estrutura um vetor de tamanho 1, cujo primeiro elemento indica

a quantidade de linhas da matriz e o segundo indica a quantidade de colunas.

Como exemplo, considere a matriz retangular X de tamanho 5× 4:

84

1 X = lmivar(2,[5 4]);

� tipo = 3: estruturas gerais. Este tipo representa matrizes mais complexas,

que nao serao tratadas nesse trabalho.

Apos a definicao das variaveis, o proximo passo e definir a LMI. Isso e feito com o

comando lmiterm(ID,A,B,flag). Os 3 primeiros argumentos desse comando sao

obrigatorios e o argumento flag e opcional. O primeiro argumento ID e um vetor

de dimensao 1 × 4. O primeiro elemento desse vetor indica qual LMI esta sendo

definida, o segundo e terceiro elementos indicam a posicao do termo que esta sendo

definido e o quarto elemento indica qual variavel esta envolvida no termo definido (X

quando envolve a variavel X, 0 quando nao envolve nenhuma variavel e -X quando

envolve XT ). Os argumentos A e B sao os termos que irao multiplicar a variavel a

esquerda e a direita, respectivamente. O argumento opcional flag pode ter o valor

como ’s’, o que torna possıvel definir o termo e seu termo simetrico de forma mais

rapida.

Uma observacao importante a ser feita e que devem ser especificados apenas os

termos nos blocos diagonais ou os termos acima da diagonal da LMI. Como a LMI

deve ser simetrica para ser resolvida com sucesso no LMI Control Toolbox, e suficiente

especificar apenas esses termos. Especificar todos os termos da LMI resulta em

termos duplicados e, portanto, cria uma LMI diferente da esperada.

O ultimo passo para definicao do problema e a criacao da representacao interna

da LMI. Isto e feito com o comando getlmis :

1 nomeDaLMI = getlmis

Esse comando so deve ser utilizado uma vez e apenas apos a declaracao de todas

as variaveis e termos da LMI com os dois comandos anteriores.

Tendo a LMI definida, o ultimo passo e resolve-la. Para isso, o toolbox possui tres

solvers diferentes:

85

� feasp. Resolve o problema da admissibilidade.

� mincx. Resolve o problema do autovalor, que tambem pode ser entendido

como a minizacao de um objetivo linear.

� gevp. Resolve o problema do autovalor generalizado.

Os tres solvers tem a representacao interna da LMI como argumento e retornam

a solucao admissıvel ou otimizada do problema.

Por fim, para ser possıvel mostrar o resultado obtido, e necessario fazer uma

conversao de variaveis. Isso acontece porque durante a especificacao da LMI os

termos sao especificados como variaveis de matrizes, porem, durante o processo de

resolucao, os solvers tratam os termos como variaveis de decisao. Dessa forma,

a solucao retornada pelo solver e uma variavel de decisao e para o resultado ser

convertido para o formato correto e necessario utilizar o comando

1 dec2mat(nomeDaLMI,variavelDeDecisao,variavelDeMatriz)

Feita essa conversao, o resultado pode ser impresso no Matlab com sucesso.

O LMI Control Toolbox oferece um ambiente grafico para especificacao de LMIs, o

LMI Lab, que pode ser acessado utilizando o comando lmiedit. Apesar de facilitar

o processo de definicao do problema, o LMI Lab nao e tao flexıvel quanto o uso

do lmiterm. Devido a essa limitacao, foi preferido nao utilizar o LMI Lab nesse

trabalho.

Um exemplo de resolucao de LMI utilizando o LMI Control Toolbox sera mostrado

mais adiante.

A.2 Yalmip

No caso do Yalmip o primeiro passo e o uso do comando yalmip(’clear’). Apesar

de nao ser um comando obrigatorio para definicao de LMIs, ele limpa definicoes

86

anteriores feitas no toolbox e evita que algum valor antigo que tenha sido guardado

pelo Matlab influencie no problema atual.

Feito isso, o proximo passo e a definicao das variaveis do problema. Aqui, isso

e feito utilizando o comando sdpvar. Toda matriz quadrada definida no Yalmip e

assumida ser simetrica, nao precisando explicitar isso. Alem disso, muitos opera-

dores do Matlab podem ser aplicados diretamente a objetos criados pelo comando

sdpvar, o que simplifica a definicao de algumas matrizes especiais. Considere as

seguintes variaveis para exemplificar o uso desse comando:

1 P = sdpvar(n); % matriz simetrica

2 P = sdpvar(n,n); % matriz simetrica

3 P = sdpvar(n,n,'symmetric'); % matriz simetrica

4 M = sdpvar(n,m); % matriz retangular

5 X = diag(sdpvar(n,1)); % matriz diagonal

6 X = toeplitz(sdpvar(n,1)); % matriz de Toeplitz

Definidas as variaveis, o proximo passo e definir as restricoes impostas pela LMI.

No Yalmip isso e feito de forma bem simples e clara. Considere o exemplo onde a

restricao requer que a variavel X seja positiva definida e a variavel Y seja negativa

definida.

1 X = sdpvar(n,n);

2 Y = sdpvar(m,m);

3 LMI = [X > 0, Y < 0];

Uma vez que todas as variaveis e restricoes estejam definidas, basta resolver o pro-

blema. Isto e feito utilizando o comando optimize(restricoes,objetivo,opcoes).

Caso o problema tratado seja o problema de admissibilidade, o argumento objetivo

pode ser omitido. O argumento opcoes e opcional, porem permite selecionar opcoes

alem das padroes no Yalmip, como escolher o solver por exemplo. A escolha das

opcoes e feita por um segundo comando, o sdpsettings.

Feita a otimizacao do problema, o ultimo passo e extrair o valor numerico da

variavel, de forma que seja possıvel exibir o valor obtido no Matlab. O comando que

87

realiza essa operacao e o comando value(variavel). Considere o exemplo linear

simples para ilustrar o uso desses 3 comandos:

min cTx sujeito a Ax ≤ b

Esse problema pode ser resolvido com o seguinte codigo:

1 x = sdpvar(length(c),1);

2 restricao = [A*x ≤ b];

3 objetivo = c'*x;

4 optimize(restricao,objetivo);

5 solucao = value(x)

Caso seja procurada apenas uma solucao admissıvel, o objetivo pode ser omitido:

1 optimize(restricao);

Caso deseje-se escolher o solver e definir quantas informacoes o solver ira mostrar

na saıda faz-se:

1 opcoes = sdpsettings('solver',sedumi,'verbose',0);

2 solucao = optimize(restricao,objetivo,opcoes)

3 solucao = optimze(restricao,[],opcoes) % quando deseja-se apenas uma solucao ...

admissıvel

A opcao verbose indica a quantidade de informacoes que sera exposta na saıda

do Matlab. O padrao para essa opcao e 1, que exibe uma quantidade razoavel de

informacoes, escolher a opcao como o valor 0 ira imprimir a solucao com a menor

quantidade de informacoes possıveis e escolher o valor 2 mostrara a maior quantidade

de informacoes.

O Yalmip nao possui um solver padrao, pois se baseia em solvers externos para

resolucao dos problemas de otimizacao. Quando o usuario nao especifica explici-

tamente qual o solver que deseja utilizar, o toolbox analisa o problema descrito e

seleciona o solver que acha mais apropriado para resolve-lo. Caso o melhor solver

para resolver o problema nao esteja disponıvel, o toolbox realiza a conversao do

problema para uma outra outra formulacao que possua um solver apropriado [35].

88

Nesse trabalho sao instalados os solvers SDPT3 e Sedumi para uso com Yalmip,

uma vez que ambos nao necessitam de licenca para sua utilizacao.

Um exemplo de resolucao de LMI utilizando o Yalmip sera mostrado mais adiante.

A.3 CVX

O CVX assim como o Yalmip e uma linguagem de modelagem que faz uso de

solvers externos, porem com a vantagem de incluir em sua instalacao os solvers

Sedumi e SDPT3, tendo o SDPT3 como padrao.

Para resolver as LMIs utilizando o CVX e importante que todas as declaracoes

estejam inclusas dentro do bloco que comeca pelo comando cvx begin e termina

com o comando cvx end.

O comando cvx begin deve incluir um modificador que indique o tipo de pro-

blema que sera resolvido. No caso das LMIs, o comando passa a ser cvx begin sdp,

onde o modificador sdp indica Semidefinite Programming, classe onde se encaixa a

resolucao de LMIs [34]. Alem disso, existe a possibilidade de controlar o que sera

exibido na saıda, assim como era possıvel no Yalmip utilizando verbose = 0. No

CVX isso e feito adicionando o modificador quiet ao comando begin, que passa a ter

a seguinte forma cvx begin sdp quiet.

Com o bloco definido pelos comandos begin e end, pode-se comecar a definir o

sistema de LMIs. Assim como nos outros toolboxs, o primeiro passo e a definicao

das variaveis. Isto e feito com o uso do comando variable seguido pelo nome da

variavel, seu tamanho e outras palavras chaves opcionais que definem a estrutura

da variavel. Como exemplo, considere a definicao das variaveis a seguir:

1 variable X

2 variable Y(5,4)

3 variable P(3,3) symmetric

4 variable Z(10,10) hermitian toeplitz

89

Nesse caso, X e uma variavel escalar, Y e uma matriz retangular 5× 4, P e uma

matriz quadrada simetrica e Z e uma matriz especial hermitiana e de toeplitz.

O proximo passo e definir as restricoes das LMIs. Caso a LMI trate de um pro-

blema de autovalor ou autovalor generalizado, havera um objetivo a ser minimizado

ou maximizado. Para isso, o CVX possui dois comandos: minimize e maximize.

Se nenhum objetivo for definido com esses dois comandos, assume-se que se trata

de um problema de admissibilidade, que e equivalente a realizar a minimizacao com

objetivo igual a 0.

As restricoes sao definidas de forma semelhante ao Yalmip com uma unica dife-

renca de nao ser necessario atribuir uma variavel a elas. Considere o mesmo exemplo

do Yalmip, onde a restricao requer que a variavel X seja positiva definida e a variavel

Y seja negativa definida.

1 cvx begin sdp quiet

2 variable X(n,n) symmetric

3 variable Y(m,m) symmetric

4 [X > 0, Y < 0]

5 cvx end

O processo de solucao no CVX nao possui uma funcao especıfica igual aos ou-

tros toolboxs. O comando que indica o inıcio do processo de solucao e o cvx end.

Portanto, fora do bloco com a definicao do problema ja e possıvel obter o resultado.

Isto e feito igual ao Yalmip, com a funcao value, que extrai o valor numerico da

variavel.

Um exemplo completo utilizando o CVX se encontra na proxima secao, que ira

comparar os 3 toolboxs.

A.4 Comparacao entre os Toolboxs

Pelas diferencas citadas acima, e facil perceber que a definicao do problema utili-

zando o Yalmip e o CVX e mais simples e intuitiva. Alem disso, esses dois toolboxs

90

possuem a vantagem de trabalharem com solvers mais recentes, que possuem de-

sempenho melhor ao lidar com problemas grandes, o que nao e visto nos solvers

inclusos no LMI Control Toolbox.

Um ponto positivo do LMI Control Toolbox e a possibilidade de se trabalhar com

LMIs estritas. Todavia, a dificuldade da definicao do problema imposta pelo uso do

comando lmiterm faz com que seja mais interessante o uso do CVX ou Yalmip,

uma vez que eles passam mais seguranca ao usuario do que esta sendo definido por

ele.

Considere o exemplo simples da equacao de Lyapunov para ilustrar o uso de cada

um dos toolboxs estudados:

P > 0, ATP + PA < 0 (A.1)

Essas duas inequacoes podem ser combinadas na LMI:

ATP + PA 0

0 −P

< 0 (A.2)

O codigo abaixo mostra como e resolvida a LMI com o LMI Control Toolbox e o

resultado obtido.

1 clear all;

2 close all;

3

4 A = [0 1;-2 -3];

5 setlmis([])

6 P = lmivar(1,[size(A,1) 1]);

7 lmiterm([1 1 1 P],1,A,'s');

8 lmiterm([1 1 2 0],1);

9 lmiterm([1 2 2 P],-1,1);

10 lmis = getlmis;

11 [tmin,Pfeas] = feasp(lmis);

12 P = dec2mat(lmis,Pfeas,P)

13

14 Resultado:

15 P = 65.9992 12.8946

16 12.8946 15.1836

91

Utilizando o Yalmip tem-se o seguinte codigo:

1 clear all;

2 close all;

3

4 A = [0 1;-2 -3];

5

6 yalmip('clear');

7 P=sdpvar(2,2);

8 LMI=[A'*P+P*A, zeros(2);zeros(2), -P] ≤ 1e-4*eye(4)

9 ops=sdpsettings('solver','sdpt3','verbose',0);

10 optimize(LMI,[],ops);

11 P=value(P)

12

13 Resultado:

14 P = 11.7628 2.2073

15 2.2073 2.8078

Utilizando o CVX, tem-se:

1 clear all;

2 close all;

3

4 A = [0 1;-2 -3];

5 cvx begin sdp quiet

6 variable P(2,2) symmetric

7 [A'*P+P*A, zeros(2);zeros(2), -P] ≤ 1e-4*eye(4)

8 cvx end

9 P=value(P)

10

11 Resultado:

12 P = 25.0780 4.7113

13 4.7113 5.9725

Com o Yalmip e CVX foi necessario fazer um ajuste para tornar a LMI estrita

em nao estrita.

Por serem ferramentas diferentes, e esperado que o resultado nao seja o mesmo.

Porem, como o caso analisado e um problema de admissibilidade, o fato de se obter

3 resultados diferentes nao e um problema, uma vez que qualquer solucao admissıvel

e uma resposta valida.

92

Por conta da dificuldade de implementacao encontrada no LMI Control Toolbox,

alem do fato de utilizar solvers mais antigos, nesse trabalho sera preferido o uso do

CVX ou do Yalmip.

93

CONTROLE DE SISTEMAS INCERTOS COM ATRASO USANDO …

Documents

Transcript of CONTROLE DE SISTEMAS INCERTOS COM ATRASO USANDO …