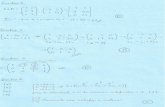MINISTRIO DA EDUCAO

INSTITUTO FEDERAL DE

EDUCAO, CINCIA E

TECNOLOGIA DE

PERNAMBUCO

PR-REITORIA DE ENSINO

DIRETORIA DE EDUCAO A

DISTNCIA

1) Considere os vetores u =(4,10,5), v1 = (1,1,2), v2 =(2,0,3) e v3 = (1,2,3).

Escreva o vetor u como combinao linear dos vetores v1, v2 e v3.

(4,10,5) = x(1,2,2) + y(2,0,3) + z(1,2,3)

(4,10,5) = (x,2x,2x) + (2y,0,3y) + (z,2z,3z)

(4,10,5) = (

Motamos um sistema lnear a aplicamos o processo de escalonamento.

{

=> {

{

=> ,

DATA: 22 / 12 /2014 Curso: LICENCIATURA EM MATEMTICA

COMPONENTE CURRICULAR:

LGEBRA LINEAR

Professor(a): Jos de Arimata

Tutores(as): Adyr Marinho, Cleiton Luis e

Fernando Galdino

{

4y = -2

x+2y+z = 4

(

) (

)

x-1-

= 4

x = 4+1+

x = 5+

x =

x =

(4,10,5) =

(1,2,2)

(2,0,3)

(1,2,3)

2)Dado o seguinte sistema:

Aplicamos o processo de escalonamento.

=> {

=>

{

{

{

-1+

10(-1+

-10 +20

=>

-1+

=>

(

=>

Logo o sistema possvel e determinado, ou seja, possui apenas uma nica

soluo, S = {2,-1,0}.

Podemos afirmar que:

a) Trata-se de um sistema impossvel.

b) Trata-se de um sistema possvel e indeterminado

c) Trata-se de um sistema possvel e determinado

d) Trata-se de um sistema homogneo.

3) Ainda em relao ao sistema da questo anterior podemos afirmar que :

a)x1 = 1, x2 = 2, x3 = 0

b) x1 = x2 = x3= 1

c) x1 = x2 e x3 =0

d) x1 = 2, x2 = -1, x3 =0

Esses valores foi encontrado anteriormente pelo processo de escalonamento,

mas pode ser encontrado pela regra de Cramer.

A = [

] => det A = |

|

|

|

[

] |

|

[

] => |

|

[

] |

|

4) Defina subespao vetorial e mostre 5 exemplos que no sejam subespao

vetorial.

Sejam V um espao vetorial e S um subconjunto no-vazio de V. O

subconjunto S

um subespao vetorial de V se S um espao vetorial em relao adio e

multiplicao por escalar definidas em V.

Um subconjunto S, no-vazio, de um espao vetorial V, um subespao

vetorial

de V se forem satisfeitas as seguintes condies:

I) Para quaisquer u,v u+v

II) Para quaisquer IR, u S, S.

EXEMPLO 1

Considere o subconjunto S do R , S ={(x,4-2x); x }

Sejam u = (1,2) e v = (0,4) . Ento:

u+v = (1,6) ou se

Portanto S no um subespao vetorial do R.

EXEMPLO 2)

Considere o subconjunto S do R , S = {(x,y) IR2/y = 4 - 2x}. Considere os

vetores u = (1,2) e v = (2,0) . Verifique que S no um subespao vetorial

u + v = (3,2) , logo no um subespao vetorial.

EEMPLO 3

Considere o subconjunto S S = {(x, |x| ); x IR} IR. Considere ainda u =

(3,3) e v = (-2,2). Mostre que S no um subespao vetorial.

u + v = (1,5) , o que mostra no ser S subespao vetorial do IR.

EXEMPLO 4

Seja V = R2 e W = f(x; x2) R2 x R), um subespao vetorial?

Se escolhermos u = (1; 1) e v = (2; 4) W, temos: u + v = (3; 5) W, portanto

W no

subespao vetorial de R2:

EXEMPLO 5

Considere o subconjunto S do R , S = {(x,y) IR y = 1 + 2x}. Considere os

vetores u = (2,5) e v = (1,3) . Verifique que S no um subespao vetorial

u + v = (3,8) , logo no um subespao vetorial.

5) Se A uma matriz 5Xm, B uma matriz 4Xn. incorreto afirmar que:

a) A operao A+B assim como B+A no est definida.

b) Se o produto A.B estiver bem definido, ento necessariamente m = 4.

c) Se o produto B.A estiver bem definido ento necessariamente n = 5

d) Se o produto B.A estiver bem definido ento necessariamente m = 4 e n = 5.

6) Coloque V para verdadeiro e F para falso.

a) ( V ) (0,1) e (1,0) so a base cannica do R. Assim um vetor

(x,y)=x(1,0)+y(0,1).

b) ( F ) (1,-1) e ( -1,2) no geram R, desta forma os vetores (x, y) no podem

ser escritos como combinao linear dos vetores mencionados.

c) ( F ) Os vetores cannicos do R so: (0,0,1); (0,1,0) e (1,0,0).

d) ( F ) O ncleo de uma transformao linear sempre o vetor nulo.

e) ( V ) Dada a seguinte transformao linear: T: V W com V um espao

finito, ento, vale o seguinte teorema: dim N(T) + dim Im(T)= dim V

7) Na diagonalizao da seguinte matriz:

Clculo dos autos valores

(

[

] [

]

[

] [

]

[

]

[

]

(4- ( (

4-

-

4-

- = - 4 =>

Podemos afirmar que:

a) Temos dois autovalores iguais.

b) A soma dos trs autovalores 10.

c) Essa matriz tem todos os seus autovalores nulos.

d) Trata-se de uma matriz triangular logo, os autovalores so os elementos

da diagonal secundaria.

8) Seja F: R R T(x,y,z)=(2x-y+z,3x+y-2z) uma funo definida do R no R.

Podemos afirmar que F uma transformao linear? Justifique sua resposta.

Sejam u = (x1, y1, z1) e v = (x2, y2, z2)

T(u+v) = T((x1, y1, z1 )+( x2, y2, z2))

T(u+v) = T(x1+ x2, y1+ y2, z1+ z2)

= 2( (x1+ x2)- (y1+ y2)+( z1+ z2),3(x1+ x2)+( y1+ y2) -2(z1+ z2))

= ( 2x1+2x2) )- (y1+ y2)+( z1+ z2), (3x1+ 3x2)+( y1+ y2)- (2z1+ 2z2))

= (2x1- y1+ z1, 3x1+ y1-2z1) + (2x2- y2+ z2, 3x2+ y2 -2z2)

= T(u) + T(v)

A primeira condio satisfeita.

T( (

= (2

(

= (

A segunda condio tambm foi satisfeita.

Assim, T verifica as duas condies e, portanto uma Transformao Linear.

Temos que T(x,y,z)=(2x-y+z,3x+y-2z) admite o vetor nulo.

T(0,0,0) = (2.0-0+0,3.0+0-2.0)

T(0,0,0) =(0,0)

9) Verifique se as afirmaes abaixo so VERDADEIRAS ou FALSAS. Se

forem verdadeiras, exiba o teorema ou propriedade. Se forem falsas, d um

contra-exemplo.

a) A multiplicao de matrizes comutativa.

FALSA

A = *

+ e B = *

+

A.B = *

+ . *

+ ( (

*

+

B. A = *

+ *

+

= *

+

LOGO AB

A propriedade comutativa no vale para a multiplicao de matizes.

b) O produto de duas matrizes no nulas pode ser uma matriz nula.

Verdadeiro

A =

e B =

A.B =

c) Todo sistema linear homogneo admite apenas a soluo trivial,

(0,0,0...,0).

VERDADEIRO

Uma equao linear homognea uma equao que possui os termos

independentes iguais a zero, por exemplo, 2x+5y-z = 0 uma equao

homognea, portanto, podemos concluir que um sistema linear ser

considerado homogneo se todas as suas equaes tiverem os seus

termos independentes iguais zero.

d) Sempre possvel calcular a inversa de uma matriz desde que a

mesma seja quadrada, ou seja, o nmero de linhas seja igual ao

nmero de colunas.

FALSA

Seja calcular a inversa de A = *

+

= *

+ e I = *

+

*

+ *

+ *

+

,

= *

+

(I) ,

(II) ,

Para (I)

,

=> ,

=> 0 = 2 (impossvel)

Se o sistema I impossvel, no h necessidade da soluo do sistema II.

Ento podemos afirmar que a matriz A no admite inversa ou que a matriz A

no invertvel ou que no singular.

10) Calcule a matriz inversa da seguinte matriz A,

A = *

+

Uma matriz quadrada A dita invertvel quando existe outra matriz denotada A-

1 tal que:

A-1 A = I

A A-1= I

onde I a matriz identidade A-1 e a matriz inversa de A.

= *

+ e I = *

+

*

+ *

+ *

+

,

= *

+

(III) ,

(IV) ,

Para( I)

2 ,

Para (II)

2 ,

2b+3d = 1

2b+3(-5) = 1

2b-15 = 1

2b = 16 => b =8

Logo a matriz inversa pedida = *

+

*

+ *

+ *

+

*

+ *

+

11) Dado o vetor V=(2,3,2) R. Pode se afirmar que V uma combinao

linear de v1 = (1,0,0), v2 = (1,1,0) R. Apresente um vetor que seja combinao

linear de v1 e v2 .

(2,3,2) = a(1,0,0)+b(1,1,0)

(2,3,2) = (a,0,0)+(b,b,0)

(2,3,2) = (a+b,b,0)

{

Sistema incompatvel, o que comprova no poder o vetor V ser escrito como

combinao linear de v1 e v2.

V no combinao linear v1 e v2.

(x,y,z) = a(1,0,0)+b(1,1,0)

(x,y,z) = (a+b,b,0)

{

V = (a+b,b,0), tomando a =1 e b = 2 por exemplo, V = (3,2,0)

Ento temos que:

(3,2,0) = (a+b,b,0)

{

z = 0

a+b = 3

a+2 = 3

a = 3-2

a =1

b = 2

(3,2,0) = a(1,0,0)+b(1,1,0)

(3,2,0) = 1.(1,0,0)+2.(1,1,0)

12) Sejam v1 = (1, 2, 5), v2 = (7, 1, 5) e v3 = (1, 1, 1) vetores do R. Esses

vetores so LI ou LD? Justifique.

x(1,2,5) +y(7,-1,5)+z(1,-1-1) = (0,0,0)

(x,2x,5x) + (7y,-y,+5y) + (z,-z,-z) = (0,0,0)

(x+7y+z,2x-y-z,5x+5y-z) = (0,0,0)

{

=> {

, como a z a incgnita livre, ou seja, z pode

assumir qualquer valor, ento os vetores so LD.

Poderemos comprovar isso escalonando o sistema

{

{

{

=> {

{

, o sistema est escalonado. Como a terceira linha o dobro

da segunda, podemos afirmar que os vetores so LD.

Tambm podemos aplicar o determinante para saber se o conjunto de vetores

so LI ou LD. Se valor do determinante for nulo, ento os vetores

considerados so LD. Caso contrrio, sero LI.

[

]

|

|

Como o determinando D= 0, o conjunto de vetores LD.