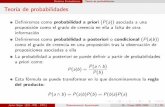
Probabilidades

1

Modelos Parametricos

Probabilidades- conceitos basicos -

2

...um pouco de historia o calculo de probabilidadesteve, eventualmente o seu inicio por volta de 1684(sec. XVII), como resultado da troca de correspondenciaentre Fermat e Pascal. A Pascal foi dito que resolve-se alguns problemas de azar.

...alguns nomes

Thomas Bayes (1708-1761) teorema de BayesJacob Bernoulli (1654-1705) lei dos grandes numerosAbraham Moivre (1667-1754) distribuicao normalPierre Simon Laplace (1748-1827) 1a sistematizacao do

calculo das probabilidadesA.N. Kolmogorov (1903-1987) Teoria Axiomatica das

probabilidades

3

Em contraste com as

experiencias deterministas, que produzem o mesmoresultado quando repetidas nas mesmas condicoes(a` mesma velocidade e durante o mesmo perodo detempo, o espaco percorrido e o mesmo, e = vt),

temos as experiencias aleatorias, em que o resultadovaria com as diferentes realizacoes da experiencia(lancar um dado, o resultado e incerto podendo ser1, 2, 3, 4, 5, 6)

As Probabilidades tratam de estudar esta realidadenao determinista (casual, aleatoria, estocastica).

4

Experiencia aleatoria:

pode ser repetida em condicoes analogas,

conhecemos todos os resultados possveis,

antes de ser realizada nao sabemos o resultadoque ira ocorrer (podemos atribuir a cada um dos resul-tados um grau de probabilidade de ocorrencia)

Exemplo:

1. lancamento de uma moeda. Que face sa?

2. lancamento de tres moedas. Qual o no de euros/caras?

3. uma caixa tem 5 bolas brancas e 5 pretas. Retiramos duasbolas em simultaneo, que cor tem?

4. lancamento de um dado. Que face sa?

5

Experiencia aleatoria:

Espaco amostral: (espaco de resultados) e consti-tudo por todos os resultados possveis,

= {R1, R2, . . . , Rn}

Exemplo:

1. = {=C, Ca}

2. = {CaCaCa,CaCa=C, Ca=C=C, Ca=CCa,=CCaCa, =CCa=C, =C=CCa, =C=C=C}

3. = {, , }

4. = {1,2,3,4,5,6}

Acontecimento: e um subconjunto qualquer do espacoamostral

A,B,C, . . . subconjuntos de Exemplo:

1. A = sada de cara

2. A = sada de duas caras = {CaCa=C, Ca=CCa, =CCaCa}

3. B = sada de bola

4. C = sada de face par = {2,4,6}

6

Acontecimento elementar: e um acontecimento comum unico modo de realizacao, isto e, constitudo porum unico elemento do espaco amostral.Exemplo:

C = sada de face 2 = {2}

Acontecimento impossvel: e um acontecimento quenunca ocorre na realizacao de uma experiencia,

Acontecimento certo: e um acontecimento que ocorresempre.Exemplo:

sada de zero no totoloto - acontecimento impossvel

sada de um no positivo no totoloto - acontecimento certo

7

Na medida em que os acontecimentos sao subcon-juntos do espaco de resultados, a` algebra de acon-tecimentos associa-se a algebra de conjuntos.

espaco amostralA A

acontecimento impossvel acontecimento certo complementar de um acontecimento A A = Aoperacoes entre acontecimentos ,,

Notas

A e o acontecimento que se realiza quando nao se realiza A,

o complementar do acontecimento certo e o acontecimento impossvel,

o complementar do acontecimento impossvel e o acontecimento certo,

A B e o acontecimento que consiste na realizacao de A ou de B,

A B e o acontecimento que consiste na realizacao de A e de B,

A e B dizem-se acontecimentos exclusivos se A B = .

8

Exemplo 1:Sejam A,B e C acontecimentos associados a uma certa ex-periencia aleatoria. Definam-se os seguintes acontecimentos:

pelo menos um dos acontecimentos ocorre

A B C

apenas ocorre o acontecimento A

A B C

ocorre exactamente um dos acontecimentos

(A B C) (B A C) (C A B)

ocorrem exactamente dois acontecimentos

(A B C) (B A C) (C A B)

9

Probabilidades

P - denota a probabilidade,

A,B,C - sao acontecimentos especficos,

P(A) - denota a probabilidade de ocorrer o acon-tecimento A,

10

Interpretacoes do conceito de probabilidade

1. Interpretacao classica

Sendo finito com n resultados possveis e A um acontecimento, obe-decendo ao princpio de simetria (todos os resultados sao igualmentepossveis)

P (A) =no casos favoraveis

no total de casos possveis=

(A)

()

Exemplo:

A: sada de face 3 num dado

P (A) = 1/6

A: sada de face par num dado

P (A) = 3/6 = 1/2

: lancamento de duas moedas

A: sada de pelo menos uma cara

P (A) = 3/4

11

2. Interpretacao frequencista

a probabilidade de um acontecimento pode ser avaliada ou estimadaobservando a frequencia relativa do mesmo acontecimento numa sucessaonumerosa de provas ou experiencias identicas e independentes

P (A) no de vezes que A ocorreno experiencias realizadas

=f

n

f : frequencia absoluta de A;

fn: frequencia relativa de A

Lei dos grandes numeros: quando uma experiencia e repetida um grandeno de vezes, o valor da frequencia relativa de um acontecimento tendea aproximar-se do valor da verdadeira probabilidade

Propriedades:

0 fn 1

fn= 1, sse A ocorre nas n provas.

3. Interpretacao axiomatica

Definicao axiomatica:

Seja o espaco amostral associado a uma experiencia aleatoria. `Afuncao que a cada acontecimento A associa um valor real P (A), quesatisfaz os seguintes axiomas, chama-se medida de probabilidade ousimplesmente probabilidade:

(i) P (A) 0 (nao negatividade)

(ii) P () = 1

(iii) P (Ai) =P (Ai) (aditividade)(se os Ai forem disjuntos dois a dois)(P (A B) = P (A) + P (B))

Propriedades:

(a) P () = 0

(b) P (A) = 1 P (A)

(c) P (A B = P (A) + P (B) P (A B) (regra da adicao)

(d) se A B entaoP (B A) = P (B) P (A)

(e) se A B entaoP (A) P (B)

Exerccio 1:Um dado e lancado 2 vezes.SejaA = {sada de um no de pintas, no 1o lanc., nao superior a 2}B = {sada de um no de pintas, no 2o lanc., superior ou igual a 5}Qual a probabilidade que se verifique A ou B?

Exerccio 2:Sabe-se que numa determinada populacao, 9.8% das pessoasadquirem a revista A, 22.9% adquirem a revista B e 5.1% am-bas as revistas.Admite-se que a medida de proporcionalidade e a proporcao deindivduos da populacao que adquirem as revistas.Defina os acontecimentos:A: adquirir a revista AB: adquirir a revista B

1. Determine a probabilidade de adquirir somente a revista A.

2. Determine a probabilidade de uma pessoa escolhida aoacaso adquirir pelo menos uma das revistas.

3. Determine a probabilidade de uma pessoa escolhida aoacaso nao adquirir nem a revista A nem a revista B.

12

1. A B = A BP (AB) = P (A)P (AB) = 0.0980.051 = 0.047

2. P (A B) = P (A) + P (B) P (A B) =0.098+ 0.229 0.051 = 0.276

3. P (A B) = 1 P (A B) = 1 0.276 = 0.724

Acontecimentos independentesDois acontecimentos dizem-se acontecimentos independentes se a realizacaode qualquer um deles nao influencia nem e influenciado pela realizacao dooutro.

Matematicamente: A e B dizem-se independentes se:

P (A B) = P (A) P (B)

Generalizando: A1, . . . , An sao acontecimentos independentes se:

P (A1 An) = P (A1) P (An)

Exemplo 1: Lancamento de um dado 2 vezes.

A: sada de face par no 1o lancamento

B: sada de face superior a 4 no 2o lancamento

Qual a probabilidade de se obter uma face par no 1o lancamento e um nosuperior a 4 no 2o lancamento?

(Estes acontecimentos sao independentes; o dado nao tem memoria)P (A) = 3/6 = 1/2; P (B) = 2/6 = 1/3; P (A B) = 6/36 = 1/6

ou, de outro modo, P (A B) = P (A).P (B) = 1/2.1/3 = 1/6

Exemplo 2: Consideremos a experiencia que consiste em retirar uma cartade um baralho de 52 cartas. Seja A o acontecimento, sada de uma copa eB o acontecimento sada de uma figura.

Os acontecimentos sao independentes?

P (A) = 13/52; P (B) = 12/52;

P (A B) = P (A\B).P (A) = 3/13 13/52

P (A).P (B) = 13/52 12/52 = 3/52

13

Probabilidade condicionalConsidere-se que se sabe que numa determinada experienciaaleatoria ocorreu um acontecimento B. Para qualquer acontec-imento A que se realize ha que considerar o facto de se ter re-alizado anteriormente B. Define-se uma nova probabilidade, efalamos de probabilidade de A dado B , ou condicional de B ,ou probabilidade de A se B .

Matematicamente: Sejam A e B acontecimentos de um espaco e

P (B) > 0. A probabilidade de A dado B e definida por:

P (A\B) = P(AB)P(B)

Nota: se B ocorreu, os unicos resultados de A que podem terocorrido sao os de A B.

14

Exemplo:

No lancamento simultaneo de 2 dados equilibrados, sejamA eB os seguintesacontecimentos:

A: sada da face 5; B: soma dos pontos igual a 7;

Qual a probabilidade de a soma dos pontos ser igual a 7, sabendo que a saiua face 5?

1 2 3 4 5 61 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

P (A) = 11/36;

P (B) = 6/36;

P (A B) = 2/36 = 1/18

P (A\B) =118636

=1

3

15

Exemplo:Numa Universidade 60% dos alunos estudam Matematica, 20% dos alunosestudam Informatica e 10% dos alunos estudam Matematica e Informatica.

Seleccionou-se aleatoriamente um aluno dessa Universidade e verificou-seque estudava Matematica. Qual a probabilidade de estudar tambem Informatica?

M = {alunos que estudam Matematica} ;P (M) = 0.6;

I = {alunos que estudam Informatica} ;P (I) = 0.2;

P (I M) = 0.1

P (I \M) =P (M I)

P (M)=

0.1

0.6=

1

6

16

Propriedades

1. Se A e B sao acontecimentos independentes,

entao A e B tambem o sao.

A = (A B) (A B)

P (A) = P (A B) + P (A B) = P (A B) + P (A).P (B),

porque A e B sao independentes

Tem-se entao P (A B) = P (A) (1 P (B)) = P (A).P (B)

2. Se A e B sao acontecimentos independentes e P (B) > 0

entao P (A \B) = P (A)

P (A \B) =P (A B)

P (B)=

P (A).P (B)

P (B)= P (A)

3. Se P (A \B) < P (A) entao P (B \A) < P (B)

P (A \B) =P (A B)

P (B)=

P (B \A).P (A)

P (B)

Se P (A \B) < P (A) = P (B \A).P (A)P (B)

< P (A)

= P (B \A) < P (B)

17

Arvores de ProbabilidadeFrequentemente precisamos de calcular a probabilidade de ocorrencia si-multanea de mais do que um acontecimento. De acordo com a probabilidadecondicional tem-se que:

P (A \B) =P (A B)

P (B)= P (A B) = P (A \B).P (B)

Podemos entao estabelecer a seguinte regra da multiplicacao

P (A1 A2 . . . An) = P (A1).P (A2 \A1).P (A3 \A1 A2) . . .

. . . P (An \A1 . . . An1)

Demonstracao:

P (A1).P (A2 \A1).P (A3 \A1 A2) . . . P (An \A1 . . . An1) =

= P (A1).P (A1 A2)

P (A1).P (A3 A2 A1)

P (A1 A2). . .

P (A1 An)

P (A1 An1)=

= P (A1 An)

Exemplo:

Um saco contem 3 bolas vermelhas, 2 bolas azuis e 5 verdes. Tiramse (semreposicao), 4 bolas desse saco.Qual a probabilidade de nenhuma das bolas ser azul?Ai: a bola i nao e azul

P (A1 A2 A3 A4) = P (A1).P (A2 \A1).P (A3 \A1 A2).

.P (A4 \A1 A2 A3)

=8

107

96

85

7=

30

90=

1

3

(Ver como se constroem arvores de probabilidades)18

Exemplo:Qual a probabilidade de nao sair a bola no 1 no concurso detotoloto (7 extraccoes sem reposicao e bolas numeradas de 1 a47)?Ai : nao sair a bola 1 na i-esima extraccaoP (A1 A2 A7) = P (A1).P (A2 \A1).P (A3 \A1 A2).P (A7 \A1 A6) =

=46

47.45

46.44

45.43

44.42

43.41

42.40

41=

40

47

19

Teorema das Probabilidades TotaisSejam A1 . . . An acontecimentos que formam uma particao deum espaco amostral (nao se intersectam e a sua uniao e oespaco).Considere-se um acontecimento B definido em .O acontecimento B nao pode ocorrer isoladamente, tera que severificar pelo menos um dos acontecimentos Aj.

Se P (Ai) > 0 entao

P (B) =

i P (B \ Ai).P (Ai)

Demonstracao:

P (B) = P (B ) = P (B (A1 A2 An)) =

= P ((B A1) (B A2) (B An))

acontecimentos mutuamente exclusivos, ja que Ai o sao= P (B A1) + P (B A2) + . . . P (B An)

= P (B \A1).P (A1) + P (B A2)P (A2) + . . . P (B An)P (An)

Exemplo:

Um aluno tem um despertador que toca na hora pretendida com probabili-dade 0.7. Se tocar, a probabilidade de o aluno acordar e 0.8, se nao tocar,a probabilidade de o aluno acordar a tempo de ir a`s aulas e 0.3. Qual aprobabilidade do aluno chegar a horas a` aula?D = o despertador toca na hora pretendida; A = o aluno acorda a tempo; H=o aluno chega a horasP (H) = P (A \D).P (D) + P (A \D).P (D) = 0.8 0.7+ 0.3 0.3

20

Teorema de BayesEste teorema e uma consequencia da definicao de probabilidade condicionale do teorema das probabilidades totais

Sejam A1 . . . An acontecimentos que formam uma particao deum espaco amostral .

Considere-se um acontecimento B, em , tal que P (B) > 0.

Entao, para cada k, k = 1, . . . , n tem-se:

P (Ak \B) =P (B \Ak).P (Ak)i P (B \ Ai).P (Ai)

Tambem conhecido como formula das probabilidades das causas permitecalcular a probabilidade do evento B ocorrer (causa) dado que A ocorreuDemonstracao:

P (Ak \B) =P (Ak B)

P (B)=

P (B \Ak)P (Ak)

B=

tendo-se pelo teorema das probabilidades totais

=P (B \Ak)P (Ak)iP (B \Ai)P (Ai)

21

Exemplo:Admita-se que, num determinado pais, em 1% da populacao tem tuberculosee, ainda que:

para uma pessoa que tenha, de facto contrado a doenca, uma micror-radiografia tem resultado positivo (isto e detecta a doenca) em 95%dos casos

para uma pessoa nao tuberculosa, esta percentagem e de apenas0.5%

Pretende-se saber qual a probabilidade de uma pessoa a quem a microrra-diografia tenha dado resultado positivo tenha tuberculose.

Consideremos os acontecimentos

T = pessoa seleccionada tem tuberculose,

T= pessoa seleccionada tem nao tuberculose,

Pos=resultado positivo

Pretende-se calcular P (T \ Pos) =?

P (T \ Pos) =P (T Pos)

P (Pos)

(faca-se a arvore das probabilidades)tem-se entao que

P (Pos) = P (Pos \T ).P (T )+P (Pos \ T ) = 0.95 0.01+0.005 0.99

Assim

P (T \ Pos) =0.95 0.001

0.95 0.01+ 0.005 0.99= 0.657 = 65.7%

22

Analise CombinatoriaA definicao classica de probabilidade (definicao de Laplace) exige o conhec-imento do no de caso favoraveis e do no de casos possveis. E pois conve-niente dispor de certas tecnicas de contagem, dizendo essencialmente re-speito ao no de subcoleccoes (ordenadas ou nao), satisfazendo uma dadadefinicao, que se podem formar a partir de um conjunto inicial.Essas tecnicas de contagem sao conhecidas por analise combinatoria.

Principio Basico da Analise Combinatoria

Se o acontecimento Ai, i = 1,2, . . . , r se pode realizar de ni maneirasdiferentes, entao o acontecimento

A1A2 . . . Ar pode realizar-se de n1n2 . . . nr maneiras.

Exemplo:

Um exame e constitudo por 12 perguntas de V/F e 5 perguntas de escolhamultipla com 4 opcoes.

De quantas maneiras diferentes e possvel responde no exame?

Consideremos os acontecimentos A1 . . . A12 referentes a`s questoes de re-spostas V/F, os quais se podem realizar de duas maneiras diferentes, isto en1 = = n12 = 2,

e os acontecimentos A13 . . . A17 referentes a`s questoes de escolha multiplaos quais se podem realizar de quatro maneiras diferentes, isto e n13 = =n17 = 4

Assim, n = 212 45 = 4194394

23

Define-se por permutacao de n objectos, o no de maneiras de dispor emlinha (sem repeticao) n objectos, o qual e igual a n!.Escreve-se:

Pn = n!

Exemplo:Quantas palavras de 4 letras podemos escrever com todas as letras da palavraMESA?

P4 = 4! = 24

Define-se por arranjos de r em n, o no de maneiras de dispor r objectos(distintos) em linha escolhidos de um total de n, o qual e igual a n!/(n r)!.Escreve-se:

Anr =n!

(nr)!

Exemplo Quantas palavras de 2 letras podemos escrever com todas as letrasda palavra MESA?

A42 =4!

2!=

4 3 2 1

2 1= 12

ExemploCom oito bandeiras diferentes, quantos sinais podem ser feitos com 3 ban-deiras diferentes?Entendendo-se que a ordem pela qual se vao apresentando as bandeiras erelevante para o sinal a realizar, tem-se que:

A83 =8!

(8 3)!= 336

24

Define-se por combinacoes de r em n, o no de maneiras de escolher robjectos (distintos) independentemente da ordem, de um total de n objectos,o qual e igual a n!

r!(n r)!.

Escreve-se:

Cnr =

(nr

)= n!

r!(nr)!

Exemplo

Num teste de 5 perguntas de quantas maneiras se podem escolher 3 pararesponder?

Considerando que Pi, i = 1,2,3,4,5, denota a pergunta i, podemos orga-nizar as perguntas do seguinte modo:

P1P2P3P1P2P4P1P2P5P1P3P4P1P3P5P1P4P5

perfaz um total de 6 possveis respostas

{P2P3P4P2P3P5P2P4P5

perfaz um total de 3 possveis respostas

{ P3P4P5 perfaz mais uma possvel resposta

Assim temos: C53 =(

53

)=

5!

3!(5 3)!=

5 4 3 2 1

3 2 1 2 1= 10

Exemplo

Qual o no possvel de resultados distintos no sorteio do totoloto?

C496 =

(496

)=

49!

6!(43)!= 13.983.816

25

Exemplo

De entre oito pessoas, quantas comissoes de 3 membros se podem formar?

Entendendo-se que duas comissoes sao iguais se forem constitudas pelasmesmas pessoas independentemente da ordem de escolha, temos que saopossveis

C38 =

(83

)=

8!

3!(5)!= 56

Define-se por arranjos com repeticao o no de maneiras de dispor r ob-jectos com repeticao em linha escolhidos de um total de n, o qual e igual anr.

Escreve-se:

Anr = n

r

Exemplo

Quantos numeros de 2 algarismos se podem formar com os algarismos 3, 5e 7?

Observando que: 3{

357

5

{357

7

{357

temos

A32 = 3

2 = 9

26

Em sntese:

No de maneiras de escolher r objectos de um total de n?

r < n?

SIM interessa a ordem

SIM com repeticao

SIM Anr = nr

N AO Anr = n!(nr)!

N AO Cnr = n!r!(nr)!N AO

27