1

MATEMÁTICA 2

Agronomia 2º P

Prof. Raquel Gondim

1. MATRIZES

Um conglomerado é composto por 5 lojas numeradas e 1 a 5. A tabela a seguir apresenta o faturamento, em

reais, nos quatro primeiros dias do mês de agosto de um determinado ano.

Qual o faturamento da loja 3 no dia 2?

Qual o faturamento total de todas as lojas no dia 3?

Qual o faturamento total da loja 1 nos 4 dias?

Podemos representar a tabela acima, abstraindo o significado de suas linhas e colunas, da seguinte maneira (que

chamamos de matriz):

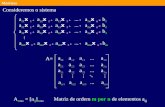
Definição 1: Um arranjo ordenado de m.n escalares aij (i=1,2,...,m; j=1,2,...,n) é denominado matriz de

dimensão m×n. As matrizes são descritas por letras maiúsculas do alfabeto romano expressas em itálico, e

assumem a forma:

Consiste em m.n elementos dispostos em m (i) linhas e n (j) colunas, que indicaremos mxnijaA )( .

Se a matriz A é de ordem m por n, costuma-se escrever simplesmente mxnA .

Os elementos de uma matriz são denominados coeficientes.

Exemplo: A matriz P abaixo fornece a quantidade de vitaminas A, B e C (representadas nas colunas) contidas

nos alimentos I e II (representados nas linhas).

A matriz é de ordem________

O elemento 12a __________

1.1 Tipos Especiais de Matrizes.

1.1.2 Matriz Nula – é aquela em que aij = 0, ∀i, ∀j.

1.1.3 Matriz Linha – é toda matriz do tipo xnijaA 1)(

2

Exemplo: A =(− 1 0 4 3). Esta matriz tem ordem 1x4.

1.1.4 Matriz Coluna – é toda matriz do tipo 1)( mxijaA

1.1.5 Matriz Retangular – é toda matriz onde .nm

Exemplo: 4/3

8

52

11A

1.1.6 Matriz Quadrada – é toda matriz do tipo nxnijaA )( , isto é, o número de linhas é igual ao número de

colunas. Neste caso, dizemos que A é uma matriz quadrada de ordem n e podemos usar a notação An.

Definições:

1. Diagonal Principal - Numa matriz quadrada A de ordem n, os elementos ija , em que i=j constituem a

diagonal principal. Exemplo: a11, a22, a33, ..., ann.

2. Diagonal Secundária - Numa matriz quadrada A de ordem n, os elementos ija , em que i+j=n+1

constituem a diagonal secundária.

Diz-se também que os elementos 7, 1 e 4 formam a diagonal secundária.

1.1.7 Matriz Diagonal – é a matriz quadrada em que os elementos que não estão na diagonal principal são

nulos.

1.1.8 Matriz Escalar – é a matriz diagonal em que os elementos da diagonal principal são iguais.

1.1.9 Matriz Identidade – é uma matriz diagonal em que os elementos da diagonal são iguais a 1. Usamos a

notação In para indicar a matriz identidade de ordem n.

Exemplos:

1.1.10 Matriz Triangular Superior – é uma matriz quadrada em que todos os elementos abaixo da diagonal

principal são nulos, isto é, a ij =0 , se i> j.

3

1.1.11 Matriz Triangular Inferior – é uma matriz quadrada em que todos os elementos acima da diagonal

principal são nulos, isto é, a ij =0 , se i< j.

1.2 Operações com Matrizes

1.2.1 Igualdade - Duas matrizes mxnijaA )( e

rxsijbB )( são iguais se possuem a mesma ordem, isto é, m = r

e n = s e aij=bij, ., ji

Exemplo: Seja 00

121

xA e

06

2

t

zyB , encontre o valor de x, y, z e t para que A=B.

1.2.3 Transposta – Dada uma matriz Amxn, denomina-se transposta de A a matriz nxmtA :

Exemplo: Seja tAA

46

53

23

1.2.4 Adição - A soma de duas matrizes de mesma ordem

mxnijaA )( e mxnijbB )( é outra matriz C de

mesma ordem mxn que denotamos por C = A + B, tal que mxnijcC )( , onde cij= aij + bij,, ., ji

Propriedades da adição:

I) Comutatividade: A + B = B + A.

II) Associatividade: A + (B + C) = (A + B) + C.

III) Elemento neutro: A + 0 = 0 + A, onde 0 representa a matriz nula.

IV) Elemento oposto: Dada a matriz A, existe a matriz oposta de A, que denotaremos por -A, tal que

A + (–A) = 0.

Exercício: Verifique que as propriedades acima são validas. (Invente as matrizes A, B e C)

Observação: A diferença A – B é a soma de A com a oposta de B, isto é A + (–B).

1.2.5 Multiplicação por um Escalar – Seja mxnijaA )( e k um escalar. Define-se a matriz B=kA, onde

mxnijbB )( , tal que bij=kaij. Isto é, multiplicam-se todos os elementos de A por k.

4

Propriedades da multiplicação por escalar:

I) k(A + B) = kA + kB.

II) (k1 + k2)A = k1A + k2A.

III) k1.(k2A) = (k1 . k2 )A.

IV) 1.A=A

Obs.: kA = Ak .

Exercícios:

1) Obter a matriz 33)( xijaA em que jiaij 3 e 33)( xijbB onde jibij 2 .

2) Usando as matrizes do exercício 1) encontre:

a) A+B

b) 2A-B

c) At

d) Bt

3) Seja a matriz ,22)( xijaA , sendo 2)( jiaij

a) Qual a ordem da matriz A? d) Para quais valores de i tem-se 0ija ?

b) Escreva o elemento 32a . e) Quais os elementos da diagonal principal?

c) Qual a transposta de A? f) Quais os elementos da diagonal secundária?

1.2.6 Multiplicação de Matrizes - Considere as matrizes mxnijaA )( e

nxpjkbB )( . O produto

mxpnxpmxn CBA . , onde nkinkijk

n

j

ijik bababac ...... 11

1

.

Obs.: De acordo com a definição, somente é possível multiplicar matrizes onde o número de colunas da

primeira é igual ao número de linhas da segunda matriz. O diagrama abaixo auxilia a interpretação.

Nem todas as matrizes podem ser multiplicadas entre si.

A ordem da multiplicação é importante.

A segunda dimensão da primeira matriz (nº de colunas) deve ser igual à primeira dimensão da segunda

matriz (nº de linhas) para que a multiplicação seja possível.

A matriz resultado terá o número de linhas da primeira matriz e o número de colunas da segunda matriz.

A multiplicação de matrizes pode ser vista como uma série de produtos internos.

5

Exemplo: Dadas as matrizes abaixo, calcule B x C

Exemplos:

1) Um corretor da bolsa de valores, calculando o patrimônio adquirido no dia por dois clientes, nas quatro

primeiras horas do pregão, montou as seguintes matrizes:

Onde:

Cada elemento a ij da matriz A é a quantidade das ações de uma empresa adquiridas pelo cliente i na hora j.

Por exemplo, o elemento a 23 =800 nos diz que foram adquiridas 800 ações pelo cliente 2 na hora 3.

Cada elemento b ij da matriz B é o preço, em dólares, de cada ação na hora i. Por exemplo, o elemento b21 nos

diz que na hora 2 o preço de cada ação era de 2,5 dólares.

Quanto investiu cada cliente para adquirir suas ações?

Esse investimento é calculado multiplicando-se o número de ações adquiridas em cada hora pelo preço unitário

e somando-se os resultados.

Cliente 1: 5000×2 + 2000× 2,5 + 1800×3 + 1000×4 = 24400.

Cliente 2: 2000×2 + 3000× 2,5 + 800×3 + 1200×4 = 18700.

Formando assim a matriz 18700

24400C

2) Sejam 210

012A e

1

2

5

1

2

4

1

1

3

B encontre A.B

3)

Propriedades da multiplicação de matrizes.

Desde que sejam possíveis os produtos entre as matrizes, são válidas as seguintes propriedades:

i) A(B ± C) = AB ± AC. (distributiva à esquerda).

ii) (A ± B)C = AC ± BC. (distributiva à direita).

iii) (AB)C = A(BC). (associativa).

iv) A.0 = 0.

Obs.:

1. Em geral ABBA ..

2. AAIIA ..

6

2. DETERMINANTES

Seja M uma matriz quadrada de ordem n. Chamamos determinante da matriz M e indicamos por det(M) (ou os

elementos da matriz entre barras verticais) o número real que obtemos operando com os elementos de M da

seguinte forma:

2.1 Cálculo do Determinante

I) Se M é de ordem n = 1 , então det(M) é o único elemento de M.

Exemplo: 2)det(22)2( AouA

II) Se M é de ordem n = 2 , então det(M) é o produto dos elementos da diagonal principal menos o produto dos

elementos da diagonal secundária.

Exemplo: 52

31A então det(A) =

III) Se M é de ordem n = 3, então det(M) é definido pela Regra de Sarrus:

Exemplos:

1) Encontre os determinantes:

a)

120

413

752

)det( A

b)

423

215

113

)det(B

2) Resolva a equação 15

102

1

132

xx

7

Principais propriedades dos determinantes.

Sejam A e B matrizes quadradas de ordem n. Então:

I) det (A) = det (AT ).

II) Se a matriz A possui fila nula, então det (A) = 0 .

III) det (λA)= λn det (A).

IV) Se a matriz A é triangular (superior ou inferior), det (A) é o produto dos elementos da diagonal principal.

V) det(A. B)= det(A). det(B).

VI) Se a matriz A tem duas linhas (ou colunas) iguais o determinante é nulo.

VII) Se 2 linhas (ou colunas) de uma matriz quadrada forem iguais ou proporcionais o determinante é nulo.

VIII) Trocando-se entre si duas linhas (ou colunas) de uma matriz o determinante muda de sinal.

IV) Se M é de ordem n > 3, então calcularemos o determinante de M usando o Teorema de Laplace. Veremos

as definições preliminares de menor complementar e cofator que serão utilizados no citado teorema.

Cofator.

Definição: Dada uma matriz A, quadrada de ordem n, *Nn e n 2 , denomina-se cofator aij o produto de ji)1( pelo determinante Dij da matriz que se obtém quando se retira de A a i-ésima linha e a j-ésima coluna.

Então: ij

ji

ij Dc .)1(

Por exemplo: 3332

232211

11

333231

232221

131211

.)1(aa

aac

aaa

aaa

aaa

A

Exemplo: Seja

1

2

5

1

2

4

1

1

3

B , calcule c11, c32, c22:

Teorema de Laplace – Dada uma matriz A, quadrada de ordem n, *Nn e n 2 . O determinante dessa matriz

é igual à soma dos produtos dos elementos de uma linha ou coluna qualquer pelos respectivos cofatores.

Exemplo: 131312121111

333231

232221

131211

...)det( acacacA

aaa

aaa

aaa

A

Exemplo: Calcule det (A), onde

126

540

312

A

Observação 1: Para calcular o determinante de uma matriz de ordem maior que 3, 1º aplica-se o Teorema de

Laplace e depois a Regra de Sarrus.

Observação 2: É melhor escolher uma fila da matriz que possua a maior quantidade de zeros com a finalidade

de simplificar os cálculos do determinante.

Exemplo: Calcular o determinante de

1422

5100

3432

0121

A

8

3. SISTEMAS LINEARES

Pense: Um caminhão pode levar no máximo 58 caixas do tipo A ou B, de mesmo tamanho. Elas têm

respectivamente 56 Kg e 72 Kg. À carga máxima para esse caminhão é de 3,84 toneladas em cada viagem.

Quantas caixas de cada tipo são transportadas, estando o caminhão com capacidade máxima?

3.1 Equação Linear Equação linear é toda equação da forma: a1x1 + a2x2+ a3x3 + ... + anxn = b

onde a1, a2, a3, ... , an são números reais, que recebem o nome de coeficientes das incógnitas

x1, x2,x3, ... , xn, e b é um número real chamado termo independente ( quando b=0, a equação recebe o nome de

linear homogênea).

Veja alguns exemplos de equações lineares:

1) 3x - 2y + 4z = 7

2) -2x + 4z = 3t - y + 4

3) (homogênea)

As equações a seguir não são lineares:

1) xy - 3z + t = 8

2) x2- 4y = 3t – 4

3)

3.2 Sistema Linear

Um conjunto de equações lineares da forma:

é um sistema linear de m equações e n incógnitas.

A solução de um sistema linear é a n-upla de números reais ordenados (r1, r2, r3,..., rn) que é,

simultaneamente, solução de todas as equações do sistema.

Exemplo 1: Verifique se (-1, 2) é solução do sistema:

13

94

ba

ba

Exemplo 2: Numa lanchonete os pastéis têm preço único e os refrigerantes também. Nesse lugar, paguei

R$ 5,80 por 5 pastéis e 3 copos de refrigerante e meu amigo pagou R$ 3,60 por 3 pastéis e 2 copos de

refrigerante. Qual o preço do pastel e refrigerante?

Vamos chamar: x o preço do pastel e y o preço do refrigerante

3.2.1 Sistemas Homogêneos

Um sistema é homogêneo quando todos os termos independentes das equações são nulos:

9

Veja um exemplo:

A n-upla (0, 0, 0,...,0) é sempre solução de um sistema homogêneo com n incógnitas e recebe o nome de

solução trivial. Quando existem, as demais soluções são chamadas não-triviais.

3.2.2 Classificação de um Sistema Quanto ao Número de Soluções

Exemplo: Resolva os sistemas lineares abaixo em ℜ2

e interprete geometricamente as soluções.

3.2.3 Matrizes Associadas a um Sistema Linear A um sistema linear podemos associar as seguintes matrizes:

matriz incompleta: a matriz A formada pelos coeficientes das incógnitas do sistema.

Em relação ao sistema:

a matriz incompleta é:

10

matriz completa: matriz B que se obtém acrescentando à matriz incompleta uma última coluna formada

pelos termos independentes das equações do sistema.

Assim, para o mesmo sistema acima, a matriz completa é:

3.2.4 Sistemas Equivalentes Dois sistemas são equivalentes quando possuem o mesmo conjunto solução.

Por exemplo, dados os sistemas:

e

Verifica-se que o par ordenado (x, y) = (1, 2) satisfaz ambos e é único.

Logo, S1 e S2 são equivalentes: S1 ~ S2.

3.2.5 Propriedades

a) Trocando de posição a equação de um sistema obtém outro sistema equivalente.

Por exemplo:

e

S1 ~S2

b) Multiplicando uma ou mais equações de um sistema por um número K (K IR*), obtém um sistema

equivalente ao anterior. Por exemplo:

S1 ~S2

c) Adicionando a uma das equações de um sistema o produto de outra equação desse mesmo sistema por um

número k ( K IR*), obtém um sistema equivalente ao anterior.

Por exemplo:

Dado , substituindo a equação (II) pela soma do produto de (I) por -1 com (II), obtém:

S1~S2, pois (x,y)=(2,1) é solução de ambos os sistemas.

3.2.6 Sistemas Escalonados Dizemos que um sistema, em que existe pelo menos um coeficiente não-nulo em cada equação, está

escalonado se o número de coeficientes nulos antes do primeiro coeficiente não nulo aumenta de equação para

equação.

Para escalonar um sistema adotamos o seguinte procedimento:

a) Fixamos como 1º equação uma das que possuem o coeficiente da 1º incógnita diferente de zero.

b) Utilizando as propriedades de sistemas equivalentes, anulamos todos os coeficientes da 1ª incógnita das

demais equações.

c) Repetimos o processo com as demais incógnitas, até que o sistema se torne escalonado.

11

Vamos então aplicar a técnica do escalonamento, considerando dois tipos de sistema:

I. O número de equações é igual ao número de incógnitas (m=n)

Exemplo 1:

1ºpasso: Anulamos todos os coeficientes da 1º incógnita a partir da 2º equação, aplicando as propriedades dos

sistemas equivalentes.

2º passo: Anulamos os coeficientes da 2º incógnita a partir da 3º equação.

3º passo: O sistema está escalonado e pode-se resolvê-lo.

Exemplo 2:

II) O número de equações é menor que o número de incógnitas (m < n)

Exemplo:

1º passo: Anulamos todos os coeficientes da 1º incógnita a partir da 2º equação.

2º passo: Anulamos os coeficientes da 2º incógnita, a partir da 3º equação.

3º passo: O sistema está escalonado. Como m<n, o sistema é possível e indeterminado, admitindo infinitas

soluções. A diferença entre o número de incógnitas (n) e o de equações (m) de um sistema nessas condições é

chamada grau de indeterminação (GI):

GI= n - m

Para resolver um sistema indeterminado, procedemos do seguinte modo:

Calculamos o grau de indeterminação do sistema nessas condições:

GI = n-m = 4-3 = 1

Como o grau de indeterminação é 1, atribuímos a uma das incógnitas um valor , supostamente conhecido, e

resolvemos o sistema em função desse valor. Sendo t= , substituindo esse valor na 3º equação.

Para cada valor que seja atribuído a , encontraremos uma quádrupla que é solução para o sistema.

3.2.7 Sistema Normal Um sistema é normal quando tem o mesmo número de equações (m) e de incógnitas (n) e o determinante da

matriz incompleta associada ao sistema é diferente de zero. Se m=n e det A 0, então o sistema é normal.

12

I) Regra de Cramer

Todo sistema normal tem uma única solução dada por:

em que i { 1,2,3,...,n}, D= det A é o determinante da matriz incompleta associada ao sistema, e Dxi é o

determinante obtido pela substituição, na matriz incompleta, da coluna i pela coluna formada pelos termos

independentes.

Discussão de um sistema linear pela Regra de Cramer

Se um sistema linear tem n equações e n incógnitas, ele pode ser:

a) Possível e determinado, se D=det A 0; caso em que a solução é única.

Exemplo:

m=n=3

Então, o sistema é possível e determinado, tendo solução única.

b) Possível e indeterminado, se D= Dx1 = Dx2 = Dx3 = ... = Dxn= 0, para n=2. Se n 3, essa condição só será

válida se não houver equações com coeficientes das incógnitas respectivamente proporcionais e termos

independentes não-proporcionais.

Um sistema possível e indeterminado apresenta infinitas soluções.

Exemplo:

D=0, Dx =0, Dy=0 e Dz=0

Assim, o sistema é possível e indeterminado, tendo infinitas soluções.

c) Impossível, se D=0 e Dxi 0, 1 i n; caso em que o sistema não tem solução.

Exemplo:

Como D=0 e Dx 0, o sistema é impossível e não apresenta solução.

4. Matriz Inversa

Seja A uma matriz quadrada de ordem n. Dizemos que A é uma matriz inversível se existir uma matriz B tal que

AB = BA = In . A matriz B é chamada de inversa da matriz A e denotada por B = 1A .

Obs.: É evidente que a matriz inversa 1A , se existir, deve ser também quadrada de ordem n, pois

1A comuta

com A.

13

Definição: Matriz singular é uma matriz quadrada que o determinante é nulo. A matriz singular não tem

inversa.

Teorema:

Onde:

Propriedades da inversa de uma matriz.

Se A e B são matrizes quadradas de ordem n e inversíveis, então:

iv) )det(

1)det( 1

AA

Exemplos:

1) Verificar se B é inversa de A, onde 23

58A e

83

52B

2) Seja 41

32A determine

1A :

3) Seja

201

110

011

A determine 1A :

Exercícios

1. Escreva a matriz em cada caso:

a) ,13)( xijaA , sendo jiaij b) ,22)( xijaA , sendo 2)( jiaij

2. Determine x e y em cada caso:

a) 04

743

04

3

xx

yx b)

030

8

030

211 xyxy

3. Dada as matrizes 345

021A e

1569

1263B , determine:

a) -2.A b) )(2

1BA

c) B+A d) -4A - tB3

2

4. Dadas as matrizes A e B, encontre o determinante de A.B:

4,1

4,1)( 43

jise

jiseacomaA ijxij e

4,1

4,1)( 34

jise

jiseacombB ijxij

1 1( )

detadjA A

A

11 12 13

21 22 23

31 32 33

( ) t

tC C C

adj C C C C

C C C

A

14

5. Encontre o determinante das matrizes em cada caso:

a)

126

540

312

B b)

1422

5100

3432

0121

C

6. Considere que se queira fazer 5 construções rurais de madeira, 7 de alvenaria e 12 mistas. O quadro as

seguir designa quanto de material será gasto em cada tipo de construção:

Tábuas Tijolos(mil) Telhas(mil) Tinta ( litros) Mão-de-obra

Madeira 200 1 5 80 12

Alvenaria 10 10 5.5 60 9

Mista 80 4 5 70 10

Quantas unidades de cada componente serão gastas?

7. Sendo as matrizesny

mxA

32 e

91

68B , achar os valores de x, y, m e n para que se tenha A=B.

8. Dadas as matrizes 108

62A ,

08

52B e

42

63C , calcular CBA 2

9. Se A = (aij) é matriz quadrada de ordem 3 tal que aij = i - j então podemos afirmar que o seu determinante é

igual a:

10. O valor de a para que a igualdade matricial 10

01

1

11.

11

12

aseja verdadeira é:

a. 1 b. 2 c. 0 d. -2 e. -1

11. Na equação 1012

3x, o valor de x é:

(A) 16 (B) 4 (C) 5 (D) 15 (E) -4

12. Sobre a matriz

431

865

431

A , marque a alternativa correta:

(A) O elemento 113a

(B) A diagonal principal é composta pelos elementos 5, 6 e 8

(C) A diagonal secundária é formada pelos elementos 1, 6 e 4

(D) A ordem da matriz transposta de A é 3x2

(E) O elemento 622a e pertence à diagonal principal

13. Sendo as matrizes3/

2

ny

mxA e

92/1

216B , os valores de x, y, m e n para que se tenha A=B, são:

14. Sobre matrizes pode-se afirmar corretamente:

a) Duas matrizes nulas são sempre iguais.

b) Toda matriz tem inversa.

c) Todas as matrizes iguais são quadradas.

d) Nem sempre podemos somar duas matrizes.

15. Se A é uma matriz 3 x 4 e B uma matriz n x m, então:

a) existe A + B se, e somente se, n = 4 e m = 3;

15

b) existe AB se, e somente se, n = 4 e m = 3;

c) existem AB e BA se, e somente se, n = 4 e m = 3;

d) existem, iguais, A + B e B + A se, e somente se, A = B;

e) existem, iguais, AB e BA se, e somente se, A = B.

16. Se A, B e C são matrizes do tipo 2x3, 3x1 e 1x4, respectivamente, então o produto A. B. C:

a. É matriz do tipo 4x2

b. É matriz do tipo 2x4

c. É matriz do tipo 3x4

d. É matriz do tipo 4x3

e. Não é definido.

17. Uma associação promoveu um show, onde compareceram 2.000 pessoas. A associação arrecadou ao todo

R$ 34.000,00, sabendo que todas as pessoas pagaram ingresso, e que cada ingresso custava R$ 20,00 e os

estudantes pagaram metade desse valor. O número de estudantes presentes no show foi:

18. Necessita-se corrigir um terreno, acrescentando a cada 10 m2

140g de nitrato, 190g de fósforo e 205g de

potássio. Dispõe-se de 4 tipos de adubo com as seguintes características por kg:

Adubo I – contém 10g de nitrato, 10g de fósforo e 100g de potássio e custa R$ 5,00

Adubo II – contém 10g de nitrato, 100g de fósforo e 30g de potássio e custa R$ 15,00

Adubo III – contém 50g de nitrato, 20g de fósforo e 20g de potássio e custa R$ 5,00

Adubo IV – contém 20g de nitrato, 40g de fósforo e 35g de potássio e custa R$ 10,00

Quanto de cada adubo deve ser misturado para conseguir o efeito desejado, podendo se gastar R$ 40,00 para

cada 10 m2 de adubação?

"São as dúvidas que nos fazem crescer, porque nos obrigam a olhar sem medo

para as muitas respostas de uma mesma pergunta."

Paulo Coelho

Bom Trabalho!!!