Matrizes
3
MINISTÉRIO DA EDUCAÇÃO COLÉGIO PEDRO II – UNIDADE SÃO CRISTÓVÃO III PROF. WALTER TADEU NOME: GABARITO DATA: 24 DE MARÇO DE 2008 TURMA: 2ª SÉRIE ATENÇÃO : Este teste pode ser realizado em grupo com até 5 alunos. O objetivo é que vocês possam discutir, entre si, possibilidades de resolução, dirimir dúvidas que ainda possuam e que individualmente não foi possível. Participem o máximo que puderem. Não desperdicem a chance de aprender com o colega. De alguma forma, mostrem sempre o desenvolvimento ou argumento na solução. Boa sorte! TESTE SOBRE MATRIZES – VALENDO 1,0 PONTO 01. Obter a matriz A = (a ij ) 2x2 definida por a ij = 3 i - j. Se a matrix é 2x2 então os valores de i e j variam de 1 a 2. Calculando os valores, temos: A 11 = 3 x 1 – 1 = 2 A 12 = 3 x 1 – 2 = 1 A 21 = 3 x 2 – 1 = 5 A 22 = 3 x 2 – 2 = 4 02. Se A é uma matriz quadrada de ordem 2 e A t sua transposta, determine A, de forma que A = 2 . A t . Temos as equações: A = e 2 x A T = a = 2a; b = 2c; c = 2b e d = 2d. Nessas condições só existe solução se: a = b = c = d = 0. Logo A é a matriz nula . 2 1 5 4 a b c d 2a 2c 2b 2d
Transcript of Matrizes
MINISTÉRIO DA EDUCAÇÃOCOLÉGIO PEDRO II – UNIDADE SÃO CRISTÓVÃO III PROF. WALTER TADEU
NOME: GABARITO
DATA: 24 DE MARÇO DE 2008 TURMA: 2ª SÉRIE
ATENÇÃO: Este teste pode ser realizado em grupo com até 5 alunos. O objetivo é que vocês possam discutir, entre si, possibilidades de resolução, dirimir dúvidas que ainda possuam e que individualmente não foi possível. Participem o máximo que puderem. Não desperdicem a chance de aprender com o colega. De alguma forma, mostrem sempre o desenvolvimento ou argumento na solução. Boa sorte!
TESTE SOBRE MATRIZES – VALENDO 1,0 PONTO
01. Obter a matriz A = (aij)2x2 definida por aij = 3 i - j.
Se a matrix é 2x2 então os valores de i e j variam de 1 a 2. Calculando os valores, temos:
A11 = 3 x 1 – 1 = 2
A12 = 3 x 1 – 2 = 1
A21 = 3 x 2 – 1 = 5
A22 = 3 x 2 – 2 = 4
02. Se A é uma matriz quadrada de ordem 2 e At sua transposta, determine A, de forma que A = 2 . At. Temos as equações: A = e 2 x AT = a = 2a; b = 2c; c = 2b e d = 2d.
Nessas condições só existe solução se: a = b = c = d = 0. Logo A é a matriz nula.
03. Se uma matriz quadrada A é tal que At = -A, ela é chamada matriz anti-simétrica. Sabe-se que M é anti-simétrica e:
Se M é anti-simétrica, então:
=
SOLUÇÃO: a12 = 4; a13 = 2 e a23 = -4
2 1
5 4
a b
c d
2a 2c
2b 2d
4+a a b
a12 b+2 c
a13 a23 2c-8
-4-a -a12 -a13
-a -b-2 -a23
-b -c -2c+8
1) 4+a = -4 –a. Logo 2a = -8 indicando a = -4.
2) a12 = -a. Logo a12 = 4.
3) b+2 = -b -2. Logo 2b = -4 indicando b = -2.
4) –a13 = b. Logo a13 = 2.
5) 2c-8 = -2c+8. Logo 4c=16 indicando c = 4 = -a23.
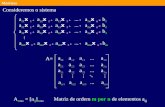
04. Na confecção de três modelos de camisas (A, B e C) são usados botões grandes (G) e pequenos (p). O número de botões por modelos é dado pela tabela:
Camisa A Camisa B Camisa C
Botões p 3 1 3
Botões G 6 5 5
O número de camisas fabricadas, de cada modelo, nos meses de maio e junho, é dado pela tabela:
Maio Junho
Camisa A 100 50
Camisa B 50 100
Camisa C 50 50
Nestas condições, obter a tabela que dá o total de botões usados em maio e junho. SOLUÇÃO: O problema se resume na multiplicação das matrizes:
X =
Maio Junho
Botões p 500 400
Botões G 1100 1050
05. Sejam as matrizes: A = (aij)4x3, aij = j.i e B = (bij)3x4, bij = j.i . Seja C a matriz resultante do produto entre A e B. Calcule elemento c23 da matriz C.
Cada elemento é calculado pelo produto de sua linha e coluna. Temos:
A X B= X
SOLUÇÃO: c23 = 2x3 + 4x6 + 6x9 = 6 + 24 + 54 = 84.
3 1 3
6 5 5
100 50
50 100
50 50
500 400
1100 1050
1 2 3
2 4 6
3 6 9
4 8 12
1 2 3 4
2 4 6 8
3 6 9 12
Não é necessário encontrar todos os resultados. Basta procurar o elemento c23 da matriz C que é calculado pela operação da 2ª linha de A com a 3ª coluna de B.
