Colectanea exercicios

DEPARTAMENTODE

ENGENHARIA MECÂNICA

MatemáticaComputacionalColectânea de Exercícios

• Propostas de resolução• Conceitos fundamentais• Algoritmos básicos• Gráficos ilustrativos

Leonel Fernandes

Miguel Matos Neves

Virgínia Infante

José Viriato

Licenciaturas em Engenharia Mecânica, Engenharia Aeroespacial eEngenharia e Arquitectura Naval - Ano Lectivo 2007/08

Para uma melhor leitura imprimir este documento em frente e verso.

ÍNDICE

TERMINOLOGIA v

2 12.1 NÚMEROS INTEIROS:

Conversão da base b para a base 10 . . . . . . . . . . . . . . . . . . . . 12.2 NÚMEROS INTEIROS:

Conversão da base b1 para a base b2 . . . . . . . . . . . . . . . . . . . 22.3 NÚMEROS REAIS:

Conversão da base 10 para a base b < 10 . . . . . . . . . . . . . . . . . 32.4 NÚMEROS REAIS:

Conversão da base b1 para a base b2

(b1 6= 10, b2 6= 10 e ambas > 2) . . . . . . . . . . . . . . . . . . . . . . 42.5 NÚMEROS REAIS:

Conversão da base 10 para base b > 10 . . . . . . . . . . . . . . . . . . 62.6 SISTEMAS DE PONTO FLUTUANTE:

Erros de representação, Unidade de arredondamento, Overflow e Un-derflow . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

3 113.1 ARITMÉTICA EM SISTEMAS FP:

Cancelamento subtractivo . . . . . . . . . . . . . . . . . . . . . . . . . 113.2 FORMATO SIMPLES IEEE 754:

Erros de representação . . . . . . . . . . . . . . . . . . . . . . . . . . . 143.3 FORMATO SIMPLES IEEE 754:

Erros de representação e Operações 0/0 e 1/0 . . . . . . . . . . . . . . 17

4 194.1 CONDICIONAMENTO DE UMA FUNÇÃO . . . . . . . . . . . . . . 194.2 CONDICIONAMENTO DE UMA FUNÇÃO E

CANCELAMENTO SUBTRACTIVO . . . . . . . . . . . . . . . . . . 204.3 INTERPOLAÇÃO POLINOMIAL:

Formas de Lagrange e Newton . . . . . . . . . . . . . . . . . . . . . . 224.4 INTERPOLAÇÃO POLINOMIAL:

Algoritmo de Horner . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24

5 275.1 INTERPOLAÇÃO POLINOMIAL:

Máximos e mínimos locais, Pontos de inflexão . . . . . . . . . . . . . . 27

ii ÍNDICE

5.2 INTERPOLAÇÃO POLINOMIAL:Interpolação de Hermite, Nós duplos e diferença dividida confluente . 31

5.3 INTERPOLAÇÃO POLINOMIAL:Interpolação de Hermite, Nós triplos e diferença dividida confluente . . 33

6 356.1 INTERPOLAÇÃO POLINOMIAL:

Spline quadrático . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 356.2 INTERPOLAÇÃO POLINOMIAL:

Spline cúbico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 376.3 INTERPOLAÇÃO POLINOMIAL:

Erros em splines cúbicos . . . . . . . . . . . . . . . . . . . . . . . . . . 41

7 437.1 DIFERENCIAÇÃO NUMÉRICA:

Diferenças finitas de primeira e segunda ordens . . . . . . . . . . . . . 437.2 DIFERENCIAÇÃO NUMÉRICA:

Majorante do erro . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 457.3 DIFERENCIAÇÃO NUMÉRICA:

Espaçamento óptimo . . . . . . . . . . . . . . . . . . . . . . . . . . . . 477.4 DIFERENCIAÇÃO NUMÉRICA:

Ponto de inflexão . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 497.5 DIFERENCIAÇÃO NUMÉRICA:

Espaçamento desigual . . . . . . . . . . . . . . . . . . . . . . . . . . . 54

8 578.1 INTEGRAÇÃO NUMÉRICA:

Regras do trapézio simples e de Simpson simples e composta . . . . . 578.2 INTEGRAÇÃO NUMÉRICA:

Regra de Gauss-Legendre e de Gauss-Legendre-Lobatto . . . . . . . . 608.3 INTEGRAÇÃO NUMÉRICA:

Regras de Gauss-Legendre e do trapézio composta . . . . . . . . . . . 61

9 659.1 INTEGRAÇÃO NUMÉRICA:

Dedução e grau de regras de integração . . . . . . . . . . . . . . . . . 659.2 INTEGRAÇÃO NUMÉRICA:

Regra do trapézio corrigida . . . . . . . . . . . . . . . . . . . . . . . . 669.3 INTEGRAÇÃO NUMÉRICA:

Regra de Simpson adaptativa iterativa . . . . . . . . . . . . . . . . . . 68

10 7510.1 DETERMINAÇÃO DE ZEROS DE EQUAÇÕES NÃO-LINEARES:

Métodos da Bissecção, Falsa Posição e Secante . . . . . . . . . . . . . 7510.2 EQUAÇÕES NÃO-LINEARES:

Método da Bissecção e zeros múltiplos . . . . . . . . . . . . . . . . . . 79

ÍNDICE iii

10.3 EQUAÇÕES NÃO-LINEARES:Método da Falsa Posição . . . . . . . . . . . . . . . . . . . . . . . . . . 80

11 8311.1 EQUAÇÕES NÃO-LINEARES:

Natureza e localização de zeros de polinómios (metodologia) . . . . . . 8311.2 EQUAÇÕES NÃO-LINEARES:

Método de Newton-Raphson . . . . . . . . . . . . . . . . . . . . . . . . 8611.3 EQUAÇÕES NÃO-LINEARES:

Método do Ponto Fixo. Localização de zeros de polinómios e aceleraçãode Aitken . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88

12 9512.1 SISTEMAS DE EQUAÇÕES LINEARES:

Método de Gauss . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9512.2 SISTEMAS DE EQUAÇÕES LINEARES:

Método de Gauss com escolha de pivot total . . . . . . . . . . . . . . . 9712.3 SISTEMAS DE EQUAÇÕES LINEARES:

Método de Gauss com escolha de pivot parcial . . . . . . . . . . . . . 101

13 10713.1 SISTEMAS DE EQUAÇÕES LINEARES:

Métodos de Doolittle e Crout. Factorização LU . . . . . . . . . . . . . 10713.2 SISTEMAS DE EQUAÇÕES LINEARES:

Factorização LU. Cálculo do determinante . . . . . . . . . . . . . . . 11113.3 SISTEMAS DE EQUAÇÕES LINEARES:

Método de Choleski e factorização LDLT . . . . . . . . . . . . . . . . 11313.4 SISTEMAS DE EQUAÇÕES LINEARES:

Método de Doolittle. Inversa, determinante e número de condição . . . 115

REFERÊNCIAS 119

TERMINOLOGIA

Listamos seguidamente as principais abreviaturas, símbolos e notação matemáticausados neste texto. No que respeita a matrizes e vectores, ambos são grafados a negro:os primeiros em maiúsculas e os segundos em minúsculas. Também incluímos umatabela com as funções elementares, seus significados e respectivas expressões usadaspela maior parte das linguagens de cálculo científico, nomeadamente em MATLAB.

Tabela de funções elementaresSÍMBOLO SIGNIFICADO EXPRESSÃO

exp x ≡ ex Exponencial de x exp(x)

ln x ≡ loge x Logaritmo natural (base e) de x log(x) ou ln(x)

cos x Co-seno de x cos(x)

cosh x ≡ (ex + e−x)/2 Co-seno hiperbólico de x cosh(x)

sin x ≡ sen x Seno de x sin(x)

sinh x ≡ (ex − e−x)/2 Seno hiperbólico de x sinh(x)

tan x ≡ tg x Tangente de x tan(x)

√x ≡ x1/2 Raiz quadrada de x sqrt(x)

|x| Valor absoluto de x abs(x)

2

TÓPICOS: Números Inteiros: Conversão da base b para a base 10; Conversãoda base b1 para a base b2. Números Reais: Conversão da base 10 para a base b < 10;Conversão da base b1 para a base b2 (b1 6= 10, b2 6= 10 e ambas > 2); Conversão da base10 para base b > 10. Sistemas de Ponto Flutuante: Erros de representação,Unidade de arredondamento, Overflow e Underflow.LEITURAS RECOMENDADAS: Capítulo 1 (pp. 1–12) do livro [Pina(1995)]

2.1 NÚMEROS INTEIROS:

Conversão da base b para a base 10

Ache a representação decimal dos seguintes números inteiros:

a) (101101)2; b) (221)3; c) (427)8

CONCEITOS TEÓRICOSNúmeros inteiros positivos: Conversão da base b ≥ 2 para a base 10† (exp. (1.2.2),

p. 4, [Pina(1995)]):

(dndn−1 . . . d1d0)b = dnbn + dn−1bn−1 + · · ·+ d1b

1 + d0b0

com 0 6 di < b− 1, i = 0, 1, . . . , n. Assim, existem (n + 1) dígitos. ¤

RESOLUÇÃOa)

(10110¸d0

1)2 = 1× 25 + 0× 24 + 1× 23 + 1× 22 + 0× 21 + 1× 20

= 32 + 8 + 4 + 1 = (45)10 = 45

No MATLAB escrevemos bin2dec(’101101’), resultando ans = 45.b)

(221)3 = 2× 32 + 2× 31 + 1× 30 = 25

†Para representar os inteiros de 0 a 10 necessitamos de quantos bits? Necessitamos de 4 bits ou16 configurações, pois 23 < 10 < 24.

2 SEMANA 2

No MATLAB escrevemos base2dec(’221’,3), resultando ans = 25.c)

(427)8 = 4× 82 + 2× 81 + 7× 80 = 4× 64 + 16 + 7 = 256 + 23 = 279

No MATLAB escrevemos base2dec(’427’,8), resultando ans = 279. ¥

2.2 NÚMEROS INTEIROS:


Obtenha a representação octal (base 8) dos números inteiros:

a) (101001)2; b) (1000111)2

CONCEITOS TEÓRICOSNúmeros inteiros positivos: Conversão da base 10 para a base b > 2 (p. 5,

[Pina(1995)]):

dnbn + dn−1bn−1 + · · ·+ d1b + d0

b= dnbn−1 + dn−1b

n−2 + · · ·+ d1 +d0

b

sendo d0 o resto da divisão. ¤

RESOLUÇÃOa) Apresentamos duas resoluções alternativas:

Resolução 1:Converter da base 2 para a base 10 e posteriormente para a base octal, ou seja,

(101001)2 → ( )10 → ( )8.

( )2 → ( )10:Aplicamos a exp. (1.2.2), p. 4, [Pina(1995)], pelo que (101001)2 = (41)10 = 41.( )10 → ( )8:(101001)2 = 41 = (51)8, pois efectuamos as divisões (inteiras) e tomamos os restos

na ordem inversa:

41 |81 5 |8

5 0

Resolução 2:Converter da base 2 para a base 2n, com n ≥ 2 e inteiro, através de agrupamentos

de n dígitos. Neste caso n = 3, pois na base 8 temos os dígitos 0, 1, 2, . . . , 6, 7, quese representam na base 2 como (000)2, (001)2, (010)2, . . . , (110)2, (111)2, respectiva-mente. Por outras palavras, necessitamos de 3 bits para representar os algarismos 0a 7. Esquematicamente temos

(101001)2 → ( )8.

EXERCÍCIOS DE MATEMÁTICA COMPUTACIONAL 3

Assim, (101 | 001)2 → (22 + 20 | 20)8 → (5 | 1)8, ou seja,

(101001)2 = (51)8b) À semelhança do que fizemos na alínea a), obtemos

Resolução 1:

(1000111)2 → (26 + 22 + 21 + 20)10 = 64 + 4 + 2 + 1 = 71 →

71 |87 8 |8

0 1 |81 0

(1000111)2 = (107)8

Resolução 2:

(001 | 000 | 111)2 → (20 | 0 | 22 + 21 + 20)8 → (1 | 0 | 7)8,ou seja (101001)2 = (107)8 ¥

2.3 NÚMEROS REAIS:

Conversão da base 10 para a base b < 10

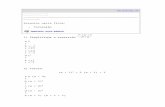
Determine a representação binária do número real (0.5)10.

CONCEITOS TEÓRICOS

Números reais: Conversão da base 10 para a base b (p. 7, [Pina(1995)]):

Para converter um real da base 10 para a base b procede-se segundo 4 passos:

i) Separar a parte inteira da parte não-inteira;

ii) Converter a parte inteira;

iii) Converter parte não-inteira, multiplicando sucessivamente por b, usando acomponente não-inteira do resultado para continuar e guardando a parte inteira paraa representação;

iv) Reunir as duas partes. ¤

RESOLUÇÃO

Aplicando os conceitos teóricos acima, teremos

i) Parte inteira: 0; Parte não-inteira: .5

ii) Converter a parte inteira: (0)10 = (0)2iii) Converter parte não-inteira:

0.5× 2 = 1.0 −→ 1

0.0× 2 = 0.

Portanto, obtemos (.1)2 como representação de (0.5)10 = 12

iv) Reunindo vem (0.5)10 = (0)2 + (.1)2 = (.1)2¥

Facilmente de verifica que (0.1)2 = 0× 20 + 1× 2−1 = 12 = (0.5)10 ¡

4 SEMANA 2

2.4 NÚMEROS REAIS:


(b1 6= 10, b2 6= 10 e ambas > 2)

Dado o número real 437.125 na base octal, determine a sua representação binária com7 dígitos após a vírgula.

CONCEITOS TEÓRICOS

Ver pp. 7–8, [Pina(1995)] e resolução do Exercício 2.3.

Números reais: Conversão da base b para a base 10 (exp. (1.3.2), p. 7, [Pina(1995)]):

(dndn−1 . . . d1d0.d−1d−2 . . . d−k)b =dnbn + dn−1bn−1 + · · ·+ d1b

1 + d0b0

+d−1b−1 + d−2b

−2 + · · ·+ d−kb−k,

sendo (dndn−1 . . . d1d0)b e (d−1d−2 . . . d−k)b os dígitos das parte inteira e não-inteirado número, respectivamente. ¤

RESOLUÇÃO

Este Exercício pode ser resolvido de duas formas, indicadas de seguida.

Resolução 1:

Esquematicamente, temos dois passos principais

(437.125)8 → ( )10 → ( )2

Conversão da base octal para a base 10:

Aplica-se a exp. (1.3.2), p. 7, [Pina(1995)], ou seja

4× 82 + 3× 81 + 7× 80 + 1× 8−1 + 2× 8−2 + 5× 8−3 = 287 + 0.166015625

= 287.166015625

Dado que devemos considerar somente 7 dígitos após a vírgula

(437.125)8 ≈ 287.1660156.

Conversão da base 10 para a base binária:


ii) Converter a parte inteira:


287 | 21 143 | 2

1 71 | 21 35 | 2

1 17 | 21 8 | 2

0 4 | 20 2 | 2

0 1 | 21 0

287 = (100011111)2

iii) Converter a parte não-inteira:

0.1660156× 2 = 0.3320312 −→ 0

0.3320312× 2 = 0.6640624 −→ 0

0.6640624× 2 = 1.3281248 −→ 1

0.3281248× 2 = 0.6562496 −→ 0

0.6562496× 2 = 1.3124992 −→ 1

0.3124992× 2 = 0.6249984 −→ 0

0.6249984× 2 = · · ·

(0.125)8 = (0.0010101 . . .)2

iv)

(437.125)8 = (100011111.0010101 . . .)2

Considerando 7 dígitos após a vírgula, o resultado é

(437.125)8 ≈ (100011111.0010101)2

Resolução 2:

Uma vez que necessitamos de 3 bits para representar os números 0 a 7 (ver Reso-lução 2 do Exercício 2.2), cada dígito do número (437.125)8 corresponde a um grupode 3 dígitos (3 bits) na base 2. Assim,

(437.125)8 = (4 | 3 | 7 | . | 1 | 2 | 5)8

→ (100 | 011 | 111 | . | 001 | 010 | 101)2

Como são pedidos 7 dígitos após a vírgula, ficamos com

(437.125)8 ≈ (100011111.0010101)2 ¥Verificação da parte não-inteira: (.0010101)2 = 1 × 2−3 + 1 × 2−5 + 1 × 2−7 =

0.1640625. Existe então um erro na representação da parte não-inteira, que deveriaser 0.166015625. Isto deve-se a termos truncado após o dígito d−7, quando seriamnecessários 9 dígitos. ¡

6 SEMANA 2

2.5 NÚMEROS REAIS:

Conversão da base 10 para base b > 10

Dado o número real 539.125 na base decimal, achar a sua representação na basehexadecimal.

CONCEITOS TEÓRICOS

Quando a base é tal que b > 10, há que recorrer a outros símbolos para represen-tar os dígitos 10, 11, 12, . . . Uma possibilidade é recorrer às letras do alfabeto latinoA,B, C, . . .

No caso da base hexadecimal ou base 16, resulta, 0, 1, . . . , 9, A,B, C, D,E, F , cor-respondendo as letras aos dígitos

A = 10, B = 11, C = 12, D = 13, E = 14, F = 15. ¤Após esta ressalva, a conversão da base 10 para a base b > 10 processa-se segundo

os quatro passos referidos nos Conceitos Teóricos do Exercício 2.3.

RESOLUÇÃO

Esquematicamente

(539.125)10 → ( )16


ii) Converter a parte inteira:

539 |1659 33 |1611 1 2 |16

2 0

539 = (21B)16

iii) Converter a parte não-inteira:

0.125× 16 = 2.0 −→ 2

0.000× 16 = 0.0 −→ 0

(0.125)10 = (0.2)16

iv) Reunindo a parte inteira à parte não-inteira fica

(539.125)10 = (21B.2)16

obtendo-se uma representação exacta. ¥


2.6 SISTEMAS DE PONTO FLUTUANTE:

Erros de representação, Unidade de arredonda-

mento, Overflow e Underflow

Considere os sistemas de ponto flutuante FP (10, 5, 2, A) e FP (10, 5, 2, T ).

a) Represente o número −327.258 nesses sistemas.

b) Qual o maior número em módulo representável nesses sistemas?

c) Qual o menor número em módulo representável nesses sistemas?

c) Calcule os erros relativos de representação e compare-os com as respectivas unidadesde arredondamento.

CONCEITOS TEÓRICOS

Um sistema FP (b, p, q) é constituído por todos os números reais x da forma([Pina(1995)], pp. 9-10)

x = ±mbt em que

b−1 6 m 6 1− b−p

|t| 6 bq − 1

e ainda x = 0.

Portanto,

x = ±(.d−1d−2d−3 . . . d−p)b±(tq−1...t1t0),

sendo p um número finito de dígitos para a mantissa e q um número finito de dígitospara o expoente, denominando-se b por base.

Salvo indicação em contrário, considera-se que a mantissa é normalizada, i.e.,d−1 6= 0, exceptuando a representação do zero.

Truncatura (T ): Desprezam-se os dígitos do número real x que não cabem namantissa, i.e., os dígitos para além dos p primeiros não são incluídos na representação.([Pina(1995)], p. 10)

Arredondamento (A): O número real x é representado pelo número do sistemaque lhe está mais próximo. ([Pina(1995)], pp. 10-11)

Limite de overflow: Maior número em módulo representável nesses sistemas, ouseja, em termos computacionais, maior número que posso guardar em memória. Estenúmero não depende de se fazer arredondamento ou truncatura.

Limite de underflow: Menor número em módulo representável nesses sistemas.Este número depende de se considerar a mantissa normalizada ou não.

Unidade de arredondamento, u: Majorante do erro relativo na representação deum número num dado sistema FP (b, p, q), tal que ([Pina(1995)], p. 12)

u =

12b1−p em FP (b, p, q, A)

b1−p em FP (b, p, q, T )

¤

8 SEMANA 2

RESOLUÇÃO

a) Concretizando para o caso em análise ficamos com

FP (10, 5, 2) : fl(x) = ±mb±t = ±(.d−1d−2d−3d−4d−5)10±(t1t0)

com 0 6 di 6 9, para i = −1,−2,−3,−4,−5.

Normalizando o número dado obtemos

x = −(.327258)10+3

verificando-se que tem 6 dígitos na mantissa.

Nos sistemas de ponto flutuante referidos teremos

fl(−327.258) = −(.32726)10+03 em FP (10, 5, 2, A)

fl(−327.258) = −(.32725)10+03 em FP (10, 5, 2, T )

b) O número limite de overflow é

(0.99999)10+99 em FP (10, 5, 2, A)

(0.99999)10+99 em FP (10, 5, 2, T )

sendo igual para T ou A.

c) Para o formato normalizado, o número limite de underflow é

(0.10000)10−99 em FP (10, 5, 2, A)

(0.10000)10−99 em FP (10, 5, 2, T )

sendo igual para T ou A.

Se tivermos um formato não normalizado este número é (0.00001)10−99. Nestecaso falamos em underflow gradual.

d) Atendendo à definição de unidade de arredondamento teremos neste caso

u =

12101−5 = (0.50000)10−4 em FP (10, 5, 2, A)

101−5 = (0.10000)10−3 em FP (10, 5, 2, T )

O erro relativo de representação é

e =x− x

x,


onde x = fl(x) é a representação no sistema de ponto flutuante e x é o número real arepresentar. Assim, os erros relativo neste caso são

∣∣∣−(0.32726)103−(−327.258)−327.258

∣∣∣ = (.61114)10−7 < (0.50000)10−4 em FP (10, 5, 2, A)

∣∣∣−(0.32725)103−(−327.258)−327.258

∣∣∣ = (.24446)10−6 < (0.10000)10−3 em FP (10, 5, 2, T )

¥

3

TÓPICOS: Aritmética em Sistemas FP: Cancelamento Subtractivo. For-mato Simples IEEE 754: Erros de representação; Erros de representação e Ope-rações 0/0 e 1/0.

LEITURAS RECOMENDADAS: Capítulo 1 (pp. 12–27) do livro [Pina(1995)]

3.1 ARITMÉTICA EM SISTEMAS FP:

Cancelamento subtractivo

Determine no sistema FP (10, 4, 2, T ) as raízes da equação

x2 + 0.7341x + (0.600)10−4 = 0

considerando que não existem dígitos de guarda† no processamento das operações emponto flutuante.

a) Usando a fórmula resolvente. Indique os erros absolutos Ex1 e Ex2 .

b) Justifique a origem do erro relativo obtido na menor raiz (em módulo) e sugirauma forma de melhoria numérica para a resolução deste problema.

CONCEITOS TEÓRICOS

As operações aritméticas no sistema de ponto flutuante FP desenvolvem-se deacordo com os seguintes passos (DAONA):‡

1. Decomposição dos operandos nas respectivas mantissas e expoentes: (mbt);

2. Alinhamento das mantissas, no caso de soma ou subtracção. Por exemplo, parat1 > t2

m1bt1 + m2b

t2 = (m1 + m2bt2−t1)bt1

(.1)10−1 + (.5)10−2 = [(.1) + (.5)10−2+1]10−1;

3. Operação com mantissas e expoentes;

4. Normalização da mantissa. Por exemplo, (1.1)10−1 = (0.11)100;

5. Arredondamento ou truncatura na mantissa.

†O processador pode ter mais dígitos que a memória, designando-se os dígitos adicionais pordígitos de guarda.

‡Em geral, as operações em FP não respeitam as propriedades comutativa, distributiva ou asso-ciativa.

12 SEMANA 3

Cancelamento subtractivo: Verifica-se quando se subtraem números muito próxi-mos no sistema de ponto flutuante utilizado. ¤

RESOLUÇÃO

a) Sabemos que

ax2 + bx + c = 0 ⇔ x1,2 =−b±√b2 − 4ac

2a

e para a = 1, é matematicamente equivalente utilizar

x2 + bx + c = 0 ⇔ x1,2 =−b±√b2 − 4c

2.

A sequência de realização deste cálculo em ponto flutuante é:

fl(b) = (.7341)100

fl(b2) = (.7341× .7341)× (100 × 100) = (.5389 *Truncar028)100 = (.5389)100

fl(c) = (.6000)10−4

fl(4) = (.4000)10+1

fl(2) = (.2000)10+1

fl(4c) = (.4000× .6000)× (10−4 × 10+1) = (.2400)10−3

fl(b2 − 4c) = (.5389)100 − (.2400)10−3

= (.5389− .0002 *100 em evidencia e truncar400)100 = (.5387)100

fl(√

b2 − 4c)

= [(.5387)100]1/2 = (.7339 :Truncar618519)100 = (.7339)100

No cálculo de√

b2 − 4c assumimos que√

x = x1/2 é uma função implementada,não sendo necessário decompô-la em funções elementares.

Para a primeira raiz:

fl(−b−

√b2 − 4c

)= −(.7341)100 − (.7339)100

= −(1.4680) ºNormalizar e truncar

|100 = −(.1468)101

fl

(−b−√b2 − 4c

2

)=−(.1468)101

(.2000)101= −(.7340)100 = fl(x1)


Para a segunda raiz:

fl(−b +

√b2 − 4c

)= −(.7341)100 + (.7339)100

= −(0.0002) ºNormalizar

|100 = −(.2000)10−3

fl

(−b +

√b2 − 4c

2

)=−(.2000)10−3

(.2000)101= −(1.) º

Normalizar

|10−4 = −(.1000)10−3 = fl(x2)

Para calcular os erros cometidos em aritmética FP é necessário conhecermos osvalores exactos das raízes, com 5 dígitos na mantissa:

x1,2 =−b±√b2 − 4c

2=−0.7341±√0.73412 − 4× 0.00006

2

x1 = −(0.73402)100 ∨ x2 = −(0.81742)10−4

pelo que os erros absolutos e relativos efectivamente cometidos são:

|Ex1 | =∣∣−(0.7340)100 − [−(0.73402)100]

∣∣ = (0.20000)10−4

|Ex2 | =∣∣−(0.1000)10−3 − [−(0.81742)10−4]

∣∣ = (0.18258)10−4,

|ex1 | =∣∣∣∣Ex1

x1

∣∣∣∣ =∣∣∣∣

(0.2000)10−4

−(0.73402)100

∣∣∣∣ = (0.27247)10−4

|ex2 | =∣∣∣∣Ex2

x2

∣∣∣∣ =∣∣∣∣

(0.18258)10−4

−(0.81742)10−4

∣∣∣∣ = (0.22336)100 ≡ 22.3%.

Apesar dos erros absolutos serem praticamente iguais, verificamos que o mesmonão acontece com o erro relativo. A segunda raiz apresenta um erro relativo superiorem quatro ordens de grandeza ao correspondente erro da primeira raiz.

b) Onde ocorreu o erro? Não aplicamos nós o mesmo processo a x1 e a x2!? Então,o que terá sucedido?

Sabemos que entre as operações +,−,×,÷, em FP existe um cálculo perigosoque é a subtracção de valores muito próximos, já que os primeiros dígitos damantissa se anulam e após a normalização surgem zeros à direita que, possivelmente,o não seriam caso se utilizasse um maior número de dígitos.

De facto, há uma subtracção de valores muito próximos quando calculamos x2 emFP (10, 4, 2, T ),

fl(−b +

√b2 − 4c

)= −(.7341)100 + (.7339)100 = −(0.0002)100

= −(.2000)10−3

14 SEMANA 3

Mas em aritmética com um maior número de dígitos na mantissa teríamos

fl(−b +

√b2 − 4c

)= −.7341 +

√.73412 − 4× 0.0006

= −(0.16348)10−3

Dividindo este número por 2 obteríamos um valor mais próximo do valor exacto.Portanto, a origem do problema no cálculo de x2 foi o cancelamento subtrac-

tivo, que se verifica quando subtraímos números muito próximos em FP.Como contornar o problema? Sabendo nós que o problema é a subtracção, o que

há a fazer é evitá-la. Existem duas alternativas:

Alternativa 1: Manipulando simbolicamente a equação de segundo grau genérica,obtemos

ax2 + bx + c = a(x− x1)(x− x2) = a(x2 − x1x− x2x + x1x2)

= ax2 − a(x1 + x2)x + ax1x2,

e concluímos que

c = ax1x2 ⇔ x2 =c

ax1.

Substituindo pelos valores conhecidos, c, a e x1, no sistema FP dado, obtemos

fl(

c

x1

)=

(.6000)10−4

−(.7340)100= −(.8174 >

Truncar38)10−4 = −(.8174)10−4 = x2.

Alternativa 2: Neste caso manipulamos a fórmula resolvente, tal que

x2 =−b +

√b2 − 4c

2=−b +

√b2 − 4c

2× −b−√b2 − 4c

−b−√b2 − 4c=

b2 − (b2 − ¸2

4c)2(−b−√b2 − 4c)

=2c

−b−√b2 − 4c=

c

x1.

Notar que obtemos a mesma expressão da alternativa 1, pois a = 1. ¥

3.2 FORMATO SIMPLES IEEE 754:

Erros de representação

a) Represente o número 512.15 em formato simples IEEE 754 com truncatura.b) Determine o erro de representação cometido na alínea anterior. Se preferir indiqueum majorante adequado do erro cometido.c) Será possível representar 10−32 e −10+42 no formato simples? Justifique.

CONCEITOS TEÓRICOSNa norma IEEE 754 a mantissa é normalizada, ou seja, o primeiro bit é sempre 1

e diz-se implícito.O expoente é enviesado, isto é, é dado por e− 127.


O maior expoente é 11111110 e o menor 00000001, estando os expoentes 11111111e 00000000 reservados para:

00000000 → Número desnormalizado, prevendo underflow gradual.

x = (−1)s(0.d−1 . . . d−23)2e−126 → Limite de underflow gradual :

2−23 × 2−126 = 2−149 = 1.4× 10−45

11111111 → Ocorrência de overflow. Neste caso podem surgir duas mensagens:

Se m = 0 → NaN

Se m 6= 0 → +INF

¤

RESOLUÇÃOa) Esquematicamente

(512.15)10 → FP (2, 24, 8, T )

pois segundo a norma IEEE 754, no formato simples, b = 2, p = 24 e q = 8.Representar a parte inteira da mantissa:

512 | 20 256 | 2

0 128 | 20 64 | 2

0 32 | 20 16 | 2

0 8 | 20 4 | 2

0 2 | 20 1 | 2

1 0

512 = (1000000000)2

Representar a parte fraccionária da mantissa:

0.15× 2 = 0.30 −→ 0

0.30× 2 = 0.60 −→ 0

0.60× 2 = 1.20 −→ 1|0.20× 2 = 0.40 −→ 0|0.40× 2 = 0.80 −→ 0|0.80× 2 = 1.60 −→ 1|0.60× 2 = 1.20 −→ 1

· · ·

16 SEMANA 3

0.15 = (0.001001 . . .)2

Representar toda a mantissa:

512.15 = (1 000 000 000.00 1001 1001 1001 . . .)2

A norma IEEE 754 requer um bit implícito de valor 1 e o expoente enviesado:

x = (−1)s2e−127(1.d−1d−2d−3 . . . d−23)2

Assim,

512.15 = (1.000 000 000 00 1001 1001 1001 :Truncar1001 . . .)2 × 29

= (1.000 000 000 00 1001 1001 1001)2 × 29

Representar o expoente (enviesado):

e− 127 = 9 ⇔ e = 136

136 | 20 68 | 2

0 34 | 20 17 | 2

1 8 | 20 4 | 2

0 2 | 20 1 | 2

1 0

136 = (10001000)2

Temos então a seguinte alocação dos 32 bits, no formato simples IEEE 754:

0 10001000 00000000000100110011001Sinal Expoente Mantissa1 bit 8 bits 23 bits

b) Erro de representação cometido:O valor exacto é

(512.15) = (1.000 000 000 00 1001 1001 1001 |1001 1001 1001 1001 . . .)2 × 29

Na norma IEEE 754 teremos o valor

(512.15)IEEE 754 = (20 + 2−12 + 2−15 + 2−16 + 2−19 + 2−20 + 2−23)× 29

= 512.1499634


e o erro em valor absoluto é

|E| = |512.1499634− 512.15| = (3.7)10−5

ou, em alternativa, podemos realizar o cálculo estimando o valor truncado

|E| = (2−24 + 2−27 + 2−28 + 2−31 + 2−32 + . . .)× 29 = (3.7)10−5

O majorante do erro cometido em truncatura é†

|E|maj = bt−p = 210−24 = 2−14 = (6.10)10−5

c) Para responder à pergunta colocada temos que determinar os limites de overflowe underflow:

Limite de overflow : (1.111 . . . 1)× 2(11111110)2−127 = (1.111 . . . 1)× 2(254−127)

= (2− 2−23)× 2127 = (3.4)10+38

Limite de underflow : (1.000 . . . 0)× 2(00000001)2−127 = (1.000 . . . 0)× 2(1−127)

= 20 × 2−126 = (1.2)10−38

Portanto,

10−32 tem representação aproximada no formato simples IEEE 754, dado que

1.2× 10−38 < 10−32 < (3.4)10+38.

10+42 não tem representação aproximada no formato simples IEEE 754, originandooverflow, pois

10+42 > (3.4)10+38.

¥

3.3 FORMATO SIMPLES IEEE 754:

Erros de representação e Operações 0/0 e 1/0

a) Estime o erro cometido na representação do número (0.1)10 no sistema de pontoflutuante FP (2, 24, 8, T ).

b) Determine o número limite de overflow e a unidade de arredondamento do sistemade ponto flutuante em formato simples na norma IEEE 754. Indique a mensagemgerada em aritmética IEEE 754 pelas operações 0/0 e 1/0.

RESOLUÇÃO

†O expoente t refere-se à representação em FP. Não esquecer que o formato IEEE 754 consideradotem um bit implícito, o que não acontece em FP. Por essa razão o expoente é 10 e não 9.

18 SEMANA 3

Representação de (0.1)10 em FP (2, 24, 8, T ):

0.1× 2 = 0.2 −→ 0

0.2× 2 = 0.4 −→ 0|0.4× 2 = 0.8 −→ 0|0.8× 2 = 1.6 −→ 1|0.6× 2 = 1.2 −→ 1|0.2× 2 = 0.4 −→ 0

· · ·

Detectamos a presença de um padrão repetitivo, ou seja,

0.1 = (0.0 0011 0011 0011 0011 0011 . . .)2

= (0.1100 1100 1100 1100 1100 1100)2 × 2−3

e pelo facto de truncar no dígito −24 obtemos um erro de representação de:

|E| = |fl(x)− x| ≈ bt−p = 2−3−24 = (7.4506)10−9

b)

Limite de overflow : (20 + 2−1 + . . . + 2−23)× 2(27+26+...21+20−127)

= (2− u)× 2127 ≈ 2128 = (3.402823)10+38

Unidade de arredondamento para truncatura : u = 21−24 = (1.192092)10−7

A 0/0 corresponde a mensagem NaN (Not a Number) e a 1/0 corresponde a men-sagem INF. ¥

A resposta na janela de comando do MATLAB para cada um dos casos é:» 0/0

Warning: Divide by zero.

(Type "warning off MATLAB:divideByZero" to suppress this warning.)

ans =

NaN

» 1/0

Warning: Divide by zero.

(Type "warning off MATLAB:divideByZero" to suppress this warning.)

ans =

Inf ¡

4

TÓPICOS: Condicionamento de uma Função. Condicionamento de

uma Função e Cancelamento Subtractivo. Interpolação Polinomial:Formas de Lagrange e Newton; Algoritmo de Horner.

LEITURAS RECOMENDADAS: Capítulo 1 (pp. 23–27) e Capítulo 2 (pp. 35–52) do livro [Pina(1995)]

4.1 CONDICIONAMENTO DE UMA FUNÇÃO

Estime o número de condição da função f (x) = tg(x2) na origem. A função é bemou mal condicionada nesse ponto? Justifique.

CONCEITOS TEÓRICOS

Número de condição da função f (x): Para analisar em aritmética de Ponto Flu-tuante a influência do erro de representação do argumento x no cálculo de uma dadafunção f (x), a Análise de Erros Directa pode não ser a mais adequada. A alternativaé uma Análise de Erros Indirecta, a qual fornece uma indicação do factor de ampli-ficação dos erros relativos baseada no número de condição de uma função num dadoponto.

Considerando que x sofre um erro de representação, o argumento utilizado nocálculo será x e o erro de representação (erro absoluto) será E = x− x. Do teoremado valor médio, e dado que x e x podem considerar-se suficientemente próximos e f

suficientemente regular, obtém-se a seguinte relação:

f (x)− f (x) = f ′ (ξ)× (x− x) ⇒ f (x)− f (x)f (x)

=f ′ (ξ)× (x− x)

f (x)× x

x

ξ ∈ [xmin − xmax] : xmin = min (x, x) e xmax = max (x, x)

∣∣∣∣f (x)− f (x)

f (x)

∣∣∣∣ ≈∣∣∣∣f ′ (x)× x

f (x)

∣∣∣∣×∣∣∣∣x− x

x

∣∣∣∣

ou, por outras palavras,

ef ≈ condf (x)× ex,

20 SEMANA 4

considerando-se geralmente no lugar de ex o valor da unidade de arredondamento u.Diz-se que uma função é bem condicionada se condf (x) for pequeno e diz-se mal

condicionada nos restantes casos.Para exemplificar melhor a distinção, recorre-se à seguinte comparação baseada

num cálculo em FP (2, 24, 8, A) onde a unidade de arredondamento é:

u =12b1−p =

1221−24 ≈ (0.6) 10−7.

Com este valor de erro relativo de representação, obtém-se no caso decondf (x) = 104 um ef = 10−3 ou seja 0.1% (f(x) é bem condicionada)e no caso decondf (x) = 106 um ef = 10−1 ou seja 10% (f(x) é mal condicionada).

Portanto, uma função ser bem condicionada ou mal condicionada é uma caracte-rística relativa. ¤

RESOLUÇÃO

condf (x) =∣∣∣∣f ′ (x)× x

f (x)

∣∣∣∣ =

∣∣∣∣∣2× x× (

1 + tg2(x2))× x

tg(x2)

∣∣∣∣∣

Lembrando-nos que na vizinhança de x = 0 se tem tg(x2) ≈ (x)2 facilmente seconclui que condf(x = 0) = 2. Uma via mais trabalhosa é fazer o que se segue!

Em x = 0, teremos

condf (x = 0) =

∣∣∣∣∣2× 02 × (

1 + tg2(02))

tg(02)

∣∣∣∣∣ =00

A indeterminação pode ser levantada aplicando sucessivamente a Regra de L’Hôpital-Cauchy:

condf (x = 0) = limx→0

∣∣∣∣2x2 + 2x2tg2(x2)

tg(x2)

∣∣∣∣

= limx→0

∣∣∣∣∣4x + 4xtg2(x2) + 8x3tg(x2)

(1 + tg2(x2)

)

2x(1 + tg2(x2)

)∣∣∣∣∣

=42

= 2

A função é bem condicionada em torno da origem, pois os erros são apenas ampli-ados para o dobro.

Por exemplo, em precisão simples — onde o majorante do erro relativo de repre-sentação de x é de aproximadamente u = (0.6)10−7 — o erro relativo no cálculo dafunção em FP será cerca de (1.2)10−7, ou seja, aproximadamente 0.000012%. ¥

4.2 CONDICIONAMENTO DE UMA FUNÇÃO E

CANCELAMENTO SUBTRACTIVO

a) Mostre que f(x) = sin(x)− x é bem condicionada na vizinhança da origem.


b) Calcule o valor de f(10−2) em FP (10, 3, 2, T ).

c) Determine os erros absolutos e relativos cometidos.

d) Em face do resultado da alínea c) proponha uma forma alternativa para o cálculode f(10−2).

RESOLUÇÃO

a) A aplicação directa da expressão origina uma indeterminação que se pode levan-tar aplicando sucessivamente a regra de L’Hôpital-Cauchy, em três aplicações. Umaalternativa é utilizar a expansão em série

cond (f) =∣∣∣∣f ′ (x) x

f (x)

∣∣∣∣ =∣∣∣∣(cos (x)− 1)x

sin (x)− x

∣∣∣∣ =

∣∣∣∣∣∣

([1− x2

2! +O (x4

)]− 1)

x[x− x3

3! +O (x5)]− x

∣∣∣∣∣∣

=

∣∣∣∣∣x3

2! +O (x5

)x3

3! +O (x5)

∣∣∣∣∣ =

∣∣∣∣∣12 +O (

x2)

16 +O (x2)

∣∣∣∣∣ ≈1216

= 3

A função é bem condicionada em torno da origem pois os erros são apenas ampli-ados para o triplo. Por exemplo, em precisão simples — onde o majorante do errorelativo de representação de x é de u = (0.6)10−7 — o erro relativo no cálculo dafunção em FP será cerca de (1.8)10−7, ou seja, aproximadamente 0.000018%.

b) Para calcular f(x) = sin(x)− x no ponto x = 10−2 em FP (10, 3, 2, T ) tem-se:

fl(x) = fl(10−2) = +(0.100)10−01

Assumindo que sin(x) esteja implementada computacionalmente como função:

fl(sin(x)) = sin(0.100× 10−01) = 0.999 :Truncar9833× 10−02 = +(0.999)10−02

fl(sin(x)− x) = 0.999× 10−02 − 0.100× 10−01 = (0.099− 0.100)ºAlinhar× 10−01

= −0.001× 10−01

= −(0.100)10−03

Como iremos ver de seguida, a truncatura para um número reduzido de dígitos,seguidamente agravada por um alinhamento das mantissas, é potencialmente perigosapara a precisão dos resultados, ocorrendo cancelamento subtractivo.

c) O valor exacto, na precisão da calculadora,† é

f(10−2) = sin(10−02)− 10−02 = −(0.16666)10−6

pelo que

E = −0.100× 10−03 − (−0.166× 10−06) = −0.000099834

†Não esquecer de efectuar os cálculos em radianos e não em graus ou grados!

22 SEMANA 4

|e| =∣∣∣∣

E

f(10−2)

∣∣∣∣ = 0.000099834/(0.16666× 10−06) = 599.03 ≡ 59903%

Obtemos, assim, um valor muito elevado.

Observa-se que f ser bem condicionada na vizinhança deste ponto não significaimune ao cancelamento subtractivo, realçando-se neste exemplo que se tratam de doisconceitos diferentes.

d) Para evitar o cancelamento subtractivo quando x é pequeno, pode utilizar-se neste caso a expansão em série da função seno:

sin (x)− x =[x− x3

3!+

x5

5!−O (

x7)]− x ≈ −x3

6

fl(sin(x) − x) = fl(−x3/6) = −(0.100 × 10−01)/(0.600 × 10+01) = 0.166 × 10−06

obtendo-se a máxima precisão em FP (10, 3, 2, T ). ¥No caso de f(x) = ln(1+x) com x < |u|, para evitar erros de FP usa-se o primeiro

termo da expansão ln(1 + x) = x− x2/2 + x3/3− x4/4 + . . .

Em MATLAB temos os logaritmos natural, log, de base 10, log10 e de base 2, log2,enquanto u é obtido por eps. ¡

4.3 INTERPOLAÇÃO POLINOMIAL:

Formas de Lagrange e Newton

Determine o polinómio interpolador dos valores (0, 1); (1, 3) e (2, 2).

a) Na forma de Lagrange.

b) Na forma de Newton com centros nos nós.

RESOLUÇÃO

a) Na forma de Lagrange este polinómio obtém-se como se segue:

n é o número de pontos, ou nós, menos 1, ou seja o grau do polinómio (desde queos pontos (xk, yk) dados não sejam colineares).

pn (x) =n∑

k=0

Lk (x) yk com Lk =n∏

i=0 i 6=k

x− xi

xk − xi

L0 =x− x1

x0 − x1

x− x2

x0 − x2

=(

x− 1−1

)(x− 2−2

)

L1 =x− x0

x1 − x0

x− x2

x1 − x2

= −x (x− 2)

L2 =x− x0

x2 − x0

x− x1

x2 − x1

=x

2(x− 1)


Obtemos:

p2(x) = L0y0 + L1y1 + L2y2

p2(x) =(x− 1) (x− 2)

2− 3x (x− 2) + x (x− 1)

Podemos verificar rapidamente que p2(0) = 1 sendo L1 = L2 = 0; p2(1) = 3 comL0 = L2 = 0 e p2(2) = 2 com L0 = L1 = 0. Tal é ilustrado pela representação gráficados polinómios na Figura 4.3.1.

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2−0.5

0

0.5

1

1.5

2

2.5

3

3.5

p(x)

L0(x)

L1(x)L2(x)

Figura 4.3.1: Polinómio interpolador e polinómios de Lagrange

b) Na forma de Newton com centros nos nós o polinómio é obtido por:

pn (x) = y [x0] + y [x0, x1] W0 + y [x0, x1, x2]W1 + ... + y [x0, x1, ..., xn]Wn−1

com

y [xk] = yk e y [xi, xi+1, ..., xk−1, xk] =y [xi+1, ..., xk]− y [xi, ..., xk−1]

xk − xi

onde as diferenças divididas se obtêm como indicado na tabela seguinte:

x y[·] y[·, ·] y[·, ·, ·]0 1

2

1 3 −3/2

−12 2

e Wi = (x− x0) . . . (x− xi−1) são os polinómios nodais.

24 SEMANA 4

O polinómio que se obtém na forma de Newton com centros nos nós é

p2(x) = 1 + 2x− 32x(x− 1)

Podemos verificar rapidamente que p2(0) = 1 sendo W0 = W1 = 0, p2(1) = 3 comW1 = 0 e p2(2) = 1 + 4− 3 = 2. Na Figura 4.3.2 observa-se a representação de p(x)e dos polinómios nodais Wi.

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2−3

−2

−1

0

1

2

3

4

p(x)

2x

1

−

3

2x(x − 1)

Figura 4.3.2: Polinómio interpolador e respectivas parcelas ¥As diferentes representações polinomiais obtidas nas alíneas a) e b) são exacta-

mente o mesmo polinómio interpolador, pois este é único (ver Teorema 2.2.2. daUnicidade, na p. 44 em [Pina(1995)]). ¡


Algoritmo de Horner

Determine o polinómio interpolador dos valores (0, -1); (1, 1); (2, 4) e (3, 2).a) Na forma de Newton com centros nos nós.b) Na forma de Lagrange.c) Calcule p(4) pelo algoritmo de Horner.

ALGORITMOSCálculo do valor do polinómio num dado ponto x através de 3 algoritmos distintos

Algoritmo 1 - Cálculo do valor de polinómios num dado ponto x:Ler/Introduzir valor de n, a0, a1, . . ., anLer/Introduzir valor de x

Inicializar p = a0Ciclo de i = 1 até n

p = p + ai× xi (1 flop soma + 1 flop produto + (i− 1) flops potência)Repetir ciclo

Escrever p

Logo o número de flops é (2 + 3 + 4 + . . . + (n + 2)) = n[(n + 2) + 2]/2 = n2/2 + 2n.


Algoritmo 2 - Técnica de Horner para cálculo do valor de um polinómio numdado ponto x:

Ler/Introduzir valor de n, a0, a1, . . ., anLer/Introduzir valor de x

Inicializar p = anCiclo de i = n - 1 até 0

p = ai + p × x (1 flop soma + 1 flop produto)

Repetir ciclo

Escrever p

Logo o número de flops é 2[(n− 1) + 1] = 2n, o que torna o algoritmo 1 «impró-prio»em termos de métodos computacionais, porque sendo o número de operações aritmé-ticas maior, considera-se também menos preciso.

Algoritmo 3 - Algoritmo de Horner para polinómios na forma de Newton comcentros nos nós:

Ler/Introduzir valor de n, a0, a1, . . ., an, c1, . . ., cnLer/Introduzir valor de x

Inicializar p = anCiclo de i = n - 1 até 0

p = ai + p × (x - ci+1) (2 flops soma + 1 flop produto)

Repetir ciclo

Escrever p

Logo o número de flops é 3[(n− 1) + 1] = 3n. ¤

RESOLUÇÃO

a) O polinómio interpolador na forma de Newton determina-se recorrendo à tabelade diferenças divididas

x y[·] y[·, ·] y[·, ·, ·] y[·, ·, ·, ·]0 −1

2

1 1 1/2

3 −1

2 4 −5/2−2

3 2

p3(x) = −1 + 2x +12x(x− 1)− x(x− 1)(x− 2)

b) A expressão para determinar o polinómio interpolador na forma de Lagrange é

pn (x) =n∑

k=0

Lk (x) yk com Lk =n∏

i=0 i 6=k

x− xi

xk − xi

26 SEMANA 4

pelo que

L0 =(

x− 1−1

)(x− 2−2

)(x− 3−3

)

L1 =x

2(x− 2)(x− 3)

L2 = −x

2(x− 1) (x− 3)

L3 =x

6(x− 1) (x− 2)

obtendo-se

p3(x) =(x− 1)(x− 2)(x− 3)

6+

x

2(x− 2)(x− 3)

− 2x(x− 1)(x− 3) +x

3(x− 1)(x− 2)

c) Aplica-se aqui o Algoritmo 3 ao polinómio da alínea a)

p3 (x) = −1 + 2x +12x (x− 1)− x (x− 1) (x− 2)

Logo n = 3 e x = 4. Precisamos também de C1 = 0, C2 = 1 e C3 = 2. Os centroscontam-se de 1 a n, não existindo C0.

Seguindo o algoritmo, obtém-se sucessivamente:

p = a3 = −1

p = a2 + p(x− C3) = (1/2) + (−1)(4− 2) = −(3/2)

p = a1 + p(x− C2) = 2− (3/2)(4− 1) = −(5/2)

p = a0 + p(x− C1) = −1− (5/2)(4− 0) = −11

Pelo que, o valor de p em x = 4 é p(4) = −11. ¥

5

TÓPICOS: Interpolação Polinomial: Máximos e mínimos locais, Pontos deinflexão; Interpolação de Hermite, Nós duplos e triplos e diferença dividida confluente.LEITURAS RECOMENDADAS: Capítulo 2 (pp. 52–73 excepto secção 2.5e pp. 77–80) do livro [Pina(1995)]


Máximos e mínimos locais, Pontos de inflexão

Considere a tabela de valores de uma função y = f(x):

x 0 1 3 4

y −21 5 −15 35

a) Determine as aproximações no intervalo [0, 4] para a localização de um máximolocal, um mínimo local e um ponto de inflexão da função.

b) Obtenha uma interpolante de f(x) na forma de Newton com centros em x0 =1/2, x1 = 1 e x2 = 3/2.

c) Se a tabela tivesse um maior número de pontos, por exemplo superior a 5, ométodo da alínea a) seria recomendável? Justifique.

RESOLUÇÃOa) As aproximações são aqui obtidas por interpolação polinomial na forma de

Newton, com centros nos nós.

x y[·] y[·, ·] y[·, ·, ·] y[·, ·, ·, ·]0 −21

26

1 5 −12

−10 8

3 −15 2050

4 35

O polinómio obtido é

p3(x) = −21 + 26(x− 0)− 12(x− 0)(x− 1) + 8(x− 0)(x− 1)(x− 3)

= −21 + 62x− 44x2 + 8x3

28 SEMANA 5

Há que ter cuidado em colocar como coeficientes do polinómio os elementos daprimeira diagonal (a negro), na ordem indicada.

Por exemplo, se escolhêssemos os elementos da diagonal inferior 35, 50, 20, 8 obte-ríamos o polinómio 35 + 50(x− 4) + 20(x− 3)(x− 4) + 8(x− 3)(x− 4)(x− 1) que éuma interpolante correcta (Porquê? Que centros foram agora utilizados?).

Deste modo, se pretendermos que os centros sejam 1, 3 e 4, deixando de fora o 0,teremos de construir uma nova tabela de diferenças divididas, tal que

x y[·] y[·, ·] y[·, ·, ·] y[·, ·, ·, ·]1 5

−10

3 −15 20

50 8

4 35 1214

0 −21

obtendo-se o polinómio:

p3(x) = 5−10(x−1)+20(x−1)(x−3)+8(x−1)(x−3)(x−4), que após expansão naforma de potências simples fica p3(x) = −21 + 62x− 44x2 + 8x3. Como esperávamos,o polinómio é o mesmo.

Podemos verificar rapidamente que as condições de interpolação são verificadaspara o polinómio obtido, pois, por exemplo, p3(0) = −21 e p3(1) = 70− 65 = 5.

0 0.5 1 1.5 2 2.5 3 3.5 4−30

−20

−10

0

10

20

30

40

Figura 5.1.1: Polinómio interpolador

As primeira e segunda derivadas do polinómio interpolador são:

p′3(x) = 62− 88x + 24x2, p′′3(x) = −88 + 48x


Donde se conclui que os pontos de estacionaridade são:

p′3(x) = 62− 88x + 24x2 = 0 ⇔ x =88±√882 − 4× 24× 62

2× 24

⇔ x1 = 0.95142 ∨ x2 = 2.7152

O ponto de inflexão é:

p′′3(x) = −88 + 48x = 0 ⇔ x = 1.8333

Como p3 é de grau 3 e p′′3 é negativa para x < 1.8333 e positiva para x > 1.8333então 0.95142 corresponde a um máximo local e 2.7152 a um mínimo local.

b) Na alínea a) obteve-se o polinómio na forma de Newton com centros nos nósda tabela. Para considerar a sua representação nos nós 1/2, 1 e 3/2 há que procedera uma mudança de nós.

Alternativa 1 - Aplicar um algoritmo de mudança de nós.

Algoritmo de Horner para mudança de centros de um polinómio (Algoritmo 2.2.2,p. 42 de [Pina(1995)]):†

Introduzir o centro c e retirar o centro cn

Ler/Introduzir valor de n, a0, a1, . . ., an, c1, . . ., cn

Inicializar a′n = an

Ciclo de i = n - 1 até 0

a′i = ai + a

′i+1 × (c - ci+1) (2 flops soma + 1 flop produto)

Repetir ciclo

Escrever a′

Utilize-se a representação com centros na origem:

p3(x) = −21 + 62x− 44x2 + 8x3

e introduzam-se sucessivamente os centros pretendidos. Tal é feito introduzindo estescentros por ordem inversa à definida.

Introdução do centro c = 3/2 (n = 3)a3 = 8 a′3 = 8

a2 = −44 c3 = 0 c = 3/2 −44 + 8× (3/2− 0) a′2 = −32

a1 = +62 c2 = 0 c = 3/2 +62− 32× (3/2− 0) a′1 = 14

a0 = −21 c1 = 0 c = 3/2 −21 + 14× (3/2− 0) a′0 = 0

p3(x) = 0 + 14 (x− 3/2)− 32 (x− 3/2) (x− 0) + 8 (x− 3/2) (x− 0)2

†O polinómio inicial deve estar na forma de potências simples.

30 SEMANA 5

Introdução do centro c = 1 (n = 3)a3 = 8 a′3 = 8

a2 = −32 c3 = 0 c = 1 −32 + 8× (1− 0) a′2 = −24

a1 = +14 c2 = 0 c = 1 +14− 24× (1− 0) a′1 = −10

a0 = 0 c1 = 3/2 c = 1 0− 10× (1− 3/2) a′0 = 5p3(x) = 5− 10(x− 1)− 24(x− 1)(x− 3/2) + 8(x− 1)(x− 3/2)(x− 0)

Introdução do centro c = 1/2 (n = 3)a3 = 8 a′3 = 8

a2 = −24 c3 = 0 c = 1/2 −24 + 8× (1/2− 0) a′2 = −20

a1 = −10 c2 = 3/2 c = 1/2 −10− 20× (1/2− 3/2) a′1 = 10

a0 = 5 c1 = 1 c = 1/2 5 + 10× (1/2− 1) a′0 = 0p3(x) = 0 + 10(x− 1/2)− 20(x− 1/2)(x− 1) + 8(x− 1/2)(x− 1)(x− 3/2)

Alternativa 2 - Como a representação polinomial é única, podemos fazer:

p3(x) = −21 + 62x− 44x2 + 8x3

p3(0.5) = −21 + 62× 0.5− 44× 0.25 + 8× 0.125 = −21 + 31− 11 + 1 = 0

p3(1.0) = −21 + 62− 44 + 8 = 5

p3(1.5) = −21 + 62× 1.5− 44× 1.52 + 8× 1.53 = 0

Utilizamos, então, estes pontos para construir a nova representação, usando comoponto auxiliar x = 3:

x y[·] y[·, ·] y[·, ·, ·] y[·, ·, ·, ·]0.5 0

10

1 5 −20

−10 8

1.5 0 0−10

3 −15

Obtemos exactamente a representação esperada devido à unicidade acima referida:p3(x) = 0 + 10(x− 1/2)− 20(x− 1/2)(x− 1) + 8(x− 1/2)(x− 1)(x− 3/2)

Omesmo sucede com o ponto auxiliar x = 4, pois, neste caso, a tabela de diferençasdivididas é

x y[·] y[·, ·] y[·, ·, ·] y[·, ·, ·, ·]0.5 0

10

1 5 −20

−10 8

1.5 0 814

4 35

ou o ponto auxiliar x = 0:


x y[·] y[·, ·] y[·, ·, ·] y[·, ·, ·, ·]0.5 0

10

1 5 −20

−10 8

1.5 0 −2414

0 −21

d) Se a tabela tivesse um maior número de pontos, por exemplo superior a 5, ométodo da alínea a) não seria recomendável porque:

- obteríamos uma equação polinomial de elevado grau cuja derivada seria morosade resolver.

- as oscilações são maiores em polinómios interpoladores de elevado grau.

Nesse caso seria preferível utilizar um método de diferenças finitas apropriadoseguido de interpolação. ¥


Interpolação de Hermite, Nós duplos e diferença

dividida confluente

a) Construa o polinómio de menor grau que interpola a função f(x) = ln(1 + x) e asua primeira derivada f ′(x) nos extremos do intervalo [0, 1].

b) Majore o erro cometido.

RESOLUÇÃO

a) Interpolar com valores de f e f ′ em cada nó corresponde à interpolação deHermite, a qual se obtém aplicando as expressões do Exemplo 2.6.1, pp. 71–72 de[Pina(1995)], [U0, U1, V0 e V1] com f(0) = 0, f(1) = ln(2), f ′(0) = 1 e f ′(1) = 1/2.

Contudo, podemos também utilizar a tabela de diferenças divididas com a técnicade nós múltiplos. De facto, da definição de diferença dividida podemos constatar que

f [x0, x1, ..., xk] =1k!

f (k) (ξ) → f [x0, x1] =f (x0)− f (x1)

(x0 − x1),

obtendo-se a diferença dividida confluente

limx1→x0

f [x0, x1] = f [x0, x0] = f ′ (x0) .

De igual modo, obtemos

f [x0, x0, x0] =f ′′ (x0)

2!.

Podemos então construir a tabela seguinte:

32 SEMANA 5

x y[·] y[·, ·] y[·, ·, ·] y[·, ·, ·, ·]0 0

1

0 0 ln(2)− 1

ln(2) 3/2− 2ln(2)1 ln(2) 1/2− ln(2)

1/21 ln(2)

p3(x) = x + [ln(2)− 1] x2 +[32− 2 ln(2)

]x2(x− 1)

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 10

0.1

0.2

0.3

0.4

0.5

0.6

0.7

(a) Polinómio0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.5

0.55

0.6

0.65

0.7

0.75

0.8

0.85

0.9

0.95

1

(b) Primeira derivada

Figura 5.2.1: Polinómio interpolador e respectiva primeira derivada

b) Análise de Erros de Interpolação - Quanto é que no máximo um polinómiointerpolador se afasta da respectiva função.

Pelo Teorema 2.4.1, p. 55, [Pina(1995)], sabemos que

en(x) ≡ f(x)− pn(x) =1

(n + 1)!f (n+1) (ξ) Wn (x)

Com base neste Teorema obtemos o majorante do erro dado por (2.4.3):

‖en‖∞ ≤ 1(n + 1)!

‖f (n+1)‖∞‖Wn‖∞

A estimativa do erro (2.4.4)

‖en‖∞ ≤ 14 (n + 1)

‖f (n+1)‖∞hn+1 =1

4 (3 + 1)6× 1 =

616

=38

= 0.3750,

não deve ser utilizada quando se pede um majorante, porque, tratando-se de umainterpolação da função e da derivada, i.e., uma interpolação de Hermite, considera-seo número de pontos apenas 2, logo n = 1, e o grau do polinómio é 2n + 1, podendomostrar-se que o erro é dado, neste caso, por (p. 73, [Pina(1995)]):


en (x) =(Wn(x))2

(2n + 2)!f (2n+2) (ξ) ≤

max[xmin,xmax]

W 2n (x)

(2n + 2)!‖f (2n+2)‖∞.

Concretizando para o caso presente, obtemos

e (x) =W 2

1 (x)(2 + 2)!

‖f (2+2) (ξ)‖∞ ≤max

x∈[0,1]

[(x− 0)2 (x− 1)2

]

24

∥∥∥[−6 (1 + x)−4

]∥∥∥∞

=116

246 =

164

= 0.15625× 10−1,

pois

f(x) = ln(1 + x)

f ′(x) = (1 + x)−1

...

f (iv) = −6(1 + x)−4

sendo∥∥f (iv)

∥∥ monótona decrescente em [−1, +∞] e, logo, no intervalo [0, 1] tem má-ximo em x = 0. ¥


Interpolação de Hermite, Nós triplos e diferença

dividida confluente

Construa o polinómio de menor grau que satisfaz as seguintes condições de interpo-lação: p(1) = 2, p′(1) = 0, p′′(1) = 2, p(2) = 2 e p(3) = 3.

RESOLUÇÃO

a) Tendo por base a definição de diferença dividida:

f [x0, x1, ..., xk] =1k!

f (k) (ξ) ,

verificamos que

f [x0, x0, x0] =f ′′ (x0)

2!.

Utilizando a tabela de diferenças finitas com a técnica de nós múltiplos (nestecaso, nó triplo):

34 SEMANA 5

x y[·] y[·, ·] y[·, ·, ·] y[·, ·, ·, ·] y[·, ·, ·, ·, ·]1 2

0

1 2 1

0 −1

1 2 0 5/8

0 1/42 2 1/2

13 3

obtemos a representação

p4(x) = 2 + (x− 1)2 − (x− 1)3 +58(x− 1)3(x− 2) ¥

Como suplemento à resolução do problema, mostramos o gráfico do polinómio eas suas primeira e segunda derivadas, obtidas analiticamente (Figuras 5.3.1 e 5.3.2 ).Observamos que as condições de interpolação são respeitadas.

1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 31.8

2

2.2

2.4

2.6

2.8

3

Figura 5.3.1: Polinómio interpolador

1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3−0.5

0

0.5

1

1.5

2

2.5

3

3.5

4

4.5

(a) Primeira derivada1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3

−2

0

2

4

6

8

10

12

14

(b) Segunda derivada

Figura 5.3.2: Derivadas analíticas do polinómio interpolador ¡

6

TÓPICOS: Interpolação Polinomial: Spline quadrático; Spline cúbico; Errosem splines cúbicos.



Spline quadrático

Construa o spline quadrático para f(x) = sin(π/2× x) em [0, 1] com malha uniformede 4 nós. Determine uma aproximação para f ′(0.5) e f ′′(0.5). Obtenha os respectivoserros absoluto e relativo.

CONCEITOS TEÓRICOS

Os splines correspondem a aproximações de funções por troços.† No caso deum spline quadrático esta aproximação é obtida entre cada dois pontos consecutivosatravés da expressão para cada subintervalo ou, mais prosaicamente, troço (Exp.(2.7.3), p. 80, [Pina(1995)]):

x ∈ [xi−1, xi], i = 1, 2, . . . , n

Si(x) = yi−1 + mi−1(x− xi−1) + Mi

2 (x− xi−1)2

Mi = mi−mi−1hi

hi = xi − xi−1

mi = 2(

yi−1−yi

hi

)−mi−1

¤

RESOLUÇÃO

Construção do spline:

Neste caso, f é contínua e continuamente diferenciável.

Uma malha uniforme, isto é, nós igualmente espaçados, com quatro pontos nointervalo [0, 1] terá os nós 0, 1/3, 2/3 e 1.

†Para uma definição mais rigorosa de splines ver p. 77 de [Pina(1995)].

36 SEMANA 6

Podemos calcular os momentos mi se conhecermos o valor de um deles. Em geralm0 define-se como m0 = f ′(x0). Neste problema temos m0 = f ′(x0) = π/2×cos(π/2×x0) = π/2 = 1.5708.

Obtemos os restantes mi aplicando a fórmula recorrente mi = 2(

yi−1−yi

hi

)−mi−1.

i xi−1 yi−1 xi yi mi−1 mi Mi

1 0 0 13 0.5 1.5708 1.4292 −0.42478

2 13 0.5 2

3 0.86602 1.4292 0.76695 −1.9868

3 23 0.86602 1 1 0.76695 0.036899 −2.1901

Então, ficamos com o spline:

x ∈ [0, 1/3] : S1 = 0 + 1.5708(x− 0) +−0.42478

2(x− 0)2

= 1.5708x− 0.2124x2

x ∈ [1/3, 2/3] : S2 = 0.5 + 1.4292(

x− 13

)+−1.9868

2

(x− 1

3

)2

= 0.5 + 1.4292(

x− 13

)− 0.99340

(x− 1

3

)2

x ∈ [2/3, 1] : S3 = 0.86602 + 0.76695(

x− 23

)+−2.1901

2

(x− 2

3

)2

= 0.86602 + 0.76695(

x− 23

)− 1.0950

(x− 2

3

)2

A Figura mostra graficamente o spline.

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 10

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

Figura 6.1.1: Spline constituído por três troços


Determinação de uma aproximação para f ′(x):

E′(0.5) = f ′(0.5)− S′(0.5) = f ′(0.5)− S′2(0.5)

= π/2× cos(π/2× 1/2)− 1.0981 = 0.012621

E′′(0.5) = f ′′(0.5)− S′′(0.5) = f ′′(0.5)− S′′2 (0.5)

= −(π/2)2 sin(π/2× 1/2) + 1.9868 = 0.24208

e′(0.5) = E′(0.5)/f ′(0.5) = 0.012621/(π/2× cos(π/2× 1/2)) = 1.1363× 10−2,

ou seja, 1.14%.

e′′(0.5) = E′′(0.5)/f ′′(0.5) = 0.24208/(−(π/2)2 sin(π/2× 1/2)) = −0.13875,

ou seja, 13.9%.f(x) e S(x) são praticamente coincidentes.Justifica-se um erro maior em S′′(0.5) do que em S′(0.5), porque nos splines

quadráticos S′(x) é linear e S′′(x) é constante por troços (Ver Figura 6.1.2).

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 10

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

(a) Primeira derivada0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

−2.5

−2

−1.5

−1

−0.5

0

0.5

1

1.5

2

(b) Segunda derivada

Figura 6.1.2: Derivadas dos três troços do spline ¥


Spline cúbico

Construir o spline cúbico que interpole os pontos: (0, 0); (0.5, 0.0625); (1, 1); (1.5, 5.0625)e (2, 16).

CONCEITOS TEÓRICOSOs splines correspondem a aproximações de funções por troços.† No caso de um

spline cúbico esta aproximação é obtida entre cada dois pontos consecutivos atravésda expressão para cada subintervalo ou, mais prosaicamente, troço (Exp. (2.7.10),

†Para uma definição mais rigorosa de splines ver p. 77 de [Pina(1995)].

38 SEMANA 6

p. 82, [Pina(1995)]):

x ∈ [xi−1, xi], i = 1, 2, . . . , n

Si(x) = Mi−1(xi−x)3

6hi+ Mi

(x−xi−1)3

6hi+

(yi−1 −Mi−1

h2i

6

)xi−x

hi+

(yi −Mi

h2i

6

)x−xi−1

hi

hi = xi − xi−1

Mi = S′′i (xi) = S′′(xi)

Os Mi, designados momentos, são dados pela exp. (2.7.13), p. 82 de [Pina(1995)]obtida impondo S′(xi−) = S′(xi+), isto é, impondo continuidade da primeira deri-vada nos nós:

hi

6Mi−1 +

hi + hi+1

3Mi +

hi+1

6Mi+1 =

yi+1 − yi

hi+1− yi − yi−1

hi,

com i = 1, 2, . . . , n− 1

Obtemos então n − 1 equações com n + 1 incógnitas Mi, i. e., M0, . . . , Mn, peloque são necessárias duas condições suplementares. Há várias possibilidades, emboraas três a seguir descritas sejam as mais usadas:

1) Spline completo: S′1(x0) = y′0, S′n(xn) = y′n.

2) Spline natural: S′′1 (x0) = M0 = 0, S′′n(xn) = Mn = 0.Este tipo de spline é indicado quando não conhecemos as derivadas y′0 e y′n. No en-tanto, estas condições podem reduzir a precisão do spline.

3) Spline periódico: y0 = yn, S′(x0) = S′(xn), M0 = Mn. ¤

RESOLUÇÃO

Construção do spline:

Neste caso vamos recorrer ao spline natural, n = 4 e hi = h = 0.5. Como oespaçamento h é constante, a expressão simplifica-se e com i = 1, 2, 3, ficamos com:

M0 = 0

12M0 + 2M1 +

12M2 = 3

(y2 − 2y1 + y0

h2

)

12M1 + 2M2 +

12M3 = 3

(y3 − 2y2 + y1

h2

)

12M2 + 2M3 +

12M4 = 3

(y4 − 2y3 + y2

h2

)

M4 = 0


ou, na forma matricial,

1 0 0 0 0

1/2 2 1/2 0 0

0 1/2 2 1/2 0

0 0 1/2 2 1/2

0 0 0 0 1

M0

M1

M2

M3

M4

=

0

3[(y2 − 2y1 + y0)/h2

]

3[(y3 − 2y2 + y1)/h2

]

3[(y4 − 2y3 + y2)/h2

]

0

Substituindo os valores de yi, i = 0, 1, 2, 3, 4 e eliminando as primeiras e últimaslinhas e colunas obtemos sucessivamente,†

2 1/2 0 10.5

1/2 2 1/2 37.5

0 1/2 2 82.5

→

2 0.5 0 10.5

0 1.875 0.5 34.875

0 0.5 2 82.5

→

→

2 0.5 0 10.5

0 1.875 0.5 34.875

0 0 1.8667 73.2

Portanto, os momentos são

M3 = 73.2/1.8667 = 39.214

M2 = (34.875− 0.5M3)/1.875 = 8.1429

M1 = (10.5− 0.5M2)/2 = 3.2143

†O leitor poderá consultar o Capítulo 12 referente a Sistemas de Equações Lineares para compre-ender a obtenção dos valores M1, M2 e M3.

40 SEMANA 6

O primeiro troço do spline corresponde a x ∈ [x0, x1], sendo

S1(x) = M0(x1 − x)3

6h+ M1

(x− x0)3

6h+

(y0 −M0

h2

6

)x1 − x

h+

(y1 −M1

h2

6

)x− x0

h

= 0 + 3.2143(x− 0)3

6× 12

+

(0− 0)0.5− x

12

+

(0.0625− 3.2143

( 12 )2

6

)x− 0

12

,

ou seja,

S1(x) = 1.0714x3 − 0.14286x para 0 6 x 6 0.5.

Os restantes troços determinam-se da mesma forma, obtendo-se

S2 = 1.6428x3 − 0.85714x2 + 0.2857x− 0.071428 para 0.5 6 x 6 1

S3 = 10.357x3 − 26.999x2 + 26.428x− 8.7857 para 1 6 x 6 1.5

S4 = −13.071x3 − 78.428x2 − 131.71x + 70.286 para 1.5 6 x 6 2

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2−2

0

2

4

6

8

10

12

14

16

Figura 6.2.1: Spline cúbico natural resultante¥



Erros em splines cúbicos

Pretende-se interpolar por um spline cúbico numa malha uniforme no intervalo [0, 1]a função f(x) = exp(1 + x). Determine o número de nós necessário para obter umerro relativo em valor absoluto inferior a 10−3.

CONCEITOS TEÓRICOS

O cálculo de erros de interpolação com splines cúbicos tem por base o Teorema2.7.4, p. 86, [Pina(1995)]:

Teorema 2.7.4: Seja f ∈ C4(Ω) e S o spline cúbico satisfazendo qualquer dascondições suplementares referidas nesta subsecção [pp. 82–83, [Pina(1995)]]. Então,

‖f − S‖∞ 6 5384

∥∥D4f∥∥∞ h4

‖D(f − S)‖∞ 6(√

3216

+124

)∥∥D4f

∥∥∞ h3

∥∥D2(f − S)∥∥∞ 6

(112

+13(h/h)

) ∥∥D4f∥∥∞ h2

∥∥D3(f − S)∥∥∞ 6 1

2(1 + (h/h)2

) ∥∥D4f∥∥∞ h

em que

h = min16i6n

hi ¤

RESOLUÇÃO

O erro relativo em valor absoluto é tal que

|e(x)| =∣∣∣∣f(x)− S(x)

f(x)

∣∣∣∣ 6 maj |f(x)− S(x)|min |f(x)|

sendo maj |f(x)− S(x)| ≡ ‖f − S‖∞.

Pelo Teorema 2.7.4, fica

5384

∥∥D4f∥∥∞ h4

min |f(x)| 6 ε = 10−3 →5

384 ‖exp(1 + x)‖∞ h4

min | exp(1 + x)| 6 ε = 10−3

⇔5

384 maxx∈[0,1]

|exp(1 + x)|h4

minx∈[0,1]

|exp(1 + x)| 6 ε = 10−3

⇔5

384 exp(2)h4

exp(1)6 ε = 10−3,

pois,∣∣D4f

∣∣ = exp(1 + x) é monótona crescente no intervalo [0,+∞] e, logo, tem ummínimo em x = 0 e um máximo em x = 1 no intervalo [0, 1].

42 SEMANA 6

Assim, resulta

h <

(10−3 exp(1)

5384 exp(2)

)1/4

h < 0.40998 → h =b− a

N=

1− 0N

< 0.40998 → N > 2.43914,

ou seja, 3 intervalos. Assim, são necessários pelo menos 4 nós. ¥

7

TÓPICOS: Diferenciação Numérica: Diferenças finitas de primeira e segundaordens; Majorante do erro; Espaçamento óptimo; Ponto de inflexão; Espaçamentodesigual.LEITURAS RECOMENDADAS: Capítulo 3 (pp. 97–111) do livro [Pina(1995)]

7.1 DIFERENCIAÇÃO NUMÉRICA:

Diferenças finitas de primeira e segunda ordens

Considere a seguinte tabela de valores para a função y = cosh x:

x 0.1 0.2 0.3 0.4

y 1.0050 1.0201 1.0453 1.0811

Determine os valores de f ′(0.2) e f ′′(0.2) pelas várias fórmulas de diferenças finitase compare os resultados com os valores exactos.

CONCEITOS TEÓRICOSConsultar as Secções 3.2 e 3.3 de [Pina(1995)]. ¤

−4 −3 −2 −1 0 1 2 3 4−15

−10

−5

0

5

10

15

Figura 7.1.1: Funções cosh(x) (—) e sinh(x) (- - -)

44 SEMANA 7

RESOLUÇÃO

Valores exactos:

y = cosh x =ex + e−x

2, y′ = sinh x =

ex − e−x

2, y′′ = cosh x =

ex + e−x

2= y

y′(0.2) = sinh(0.2) = 0.20134, y′′(0.2) = cosh(0.2) = 1.0201

Valores por diferenças finitas:

Para o cálculo da primeira derivada, vamos usar diferenças finitas de primeira esegunda ordens.

Diferenças finitas de 1.a ordem Dhf(x) com h = 0.1:

Progressiva (exp. (3.2.8)) f(x+h)−f(x)h = f(0.2+0.1)−f(0.2)

0.1 = 0.2520

Regressiva (exp. (3.2.10)) f(x)−f(x−h)h = f(0.2)−f(0.2−0.1)

0.1 = 0.1510

Central (exp. (3.2.12)) f(x+h)−f(x−h)2h = f(0.2+0.1)−f(0.2−0.1)

2×0.1 = 0.2015

Diferenças finitas de 2.a ordem Dhf(x) com h = 0.1:

Progressiva (Exp. (3.2.16)) −3f(x)+4f(x+h)−f(x+2h)2h = ... = 0.1990

Regressiva (Exp. (3.2.20)) 3f(x)−4f(x−h)+f(x−2h)2h = ... = 0.20150

Central (Exp. (3.2.12)) Expressão e valor iguais a 1.a ordem

Para calcular a diferença finita regressiva de 2.a ordem precisamos de saber o valorda função em x = 0, que neste caso é f(0) = cosh(0) = 1.

A Figura abaixo mostra as tangentes, isto é, polinómios de ordem um, dados pelasdiferenças finitas de primeira ordem.


0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4

0.96

0.98

1

1.02

1.04

1.06

1.08

1.1

R

P

C

Figura 7.1.2: Diferenças Finitas: (P) Progressiva, (R) regressiva e (C) central

A melhor aproximação foi obtida com a Diferença Finita Central, e com a Dife-rença Regressiva de 2.a ordem, mas esta última requer um maior número de pontos einclusive um valor de f(x) que não está na tabela dada.

Para a segunda derivada, vamos considerar apenas a diferença finita central (ob-viamente de segunda ordem).

Exp. (3.3.1) com h = 0.1:

D2hf(x) =

f(x + h)− 2f(x) + f(x− h)h2

=f(0.3)− 2f(0.2) + f(0.1)

0.12=

1.0453− 2× 1.0201 + 1.0050.12

= 1.0100,

ou seja, sendo o valor exacto y′′(0.2) = 1.0201, esta aproximação dispõe de dois dígitoscorrectos. ¥


Majorante do erro

Obtenha o valor de f ′(1.0) para a função f(x) = exp(−x) usando diferenças finitasprogressivas e passo h = 0.001. Determine o erro efectivamente cometido e compare-ocom o majorante teórico.

CONCEITOS TEÓRICOS

Consultar as Secções 3.2 e 3.3 de [Pina(1995)]. ¤

46 SEMANA 7

RESOLUÇÃO

Valores aproximado e exacto:

Dhf(x) =f(x + h)− f(x)

h

=f(1.001)− f(1.0)

0.001=

e−1.001 − e−1

0.001= −0.3676956

f ′(x) = −ex ⇒ f ′(1.0) = −e−1.0 = −0.3678794

Erro efectivamente cometido:

E(1.0) = f ′(1.0)−Dhf(1.0) = −0.3678794− (−0.3676956)

= −0.0001838 = −(1.838)10−4

O majorante teórico do erro (erro devido apenas à aproximação da derivada) édado pela exp. (3.2.9), p. 100 de [Pina(1995)]: †

e′1(x) = −12hf ′′(ξ) em que ξ ∈ [x0, x1] = Ω

|e′1(x)| 6 12h ‖f ′′(x)‖∞

Neste problema, f ′′(x) = e−x em Ω = [1.0, 1.0 + h]. Concretizando, e atendendoa que a função é monótona, o máximo encontra-se num extremo do intervalo (verFigura 7.2.1), fica

‖f ′′(x)‖Ω∞ = f ′′(1.0) = f(1.0) = 0.367879

|e′1(1.0)| 6 12× 0.001× 0.367879 = (1.839)10−4

Constatamos que, de facto, |E(1.0)| 6 |e′1(1.0)|, sendo praticamente igual.

†Utiliza-se para o erro de interpolação a letra minúscula e de forma a manter a coerência com anomenclatura utilizada no livro de [Pina(1995)]. Note-se no entanto que se trata de um erro absolutoe por isso deveríamos utilizar uma letra maiúscula.


−1.5 −1 −0.5 0 0.5 1 1.50

0.5

1

1.5

2

2.5

3

3.5

4

4.5

Figura 7.2.1: Funções exp(−x) (—) e exp(x) (- - -) ¥


Espaçamento óptimo

Dada a seguinte tabela de tempos e posições:

t 0 1/3 2/3 1

y(t) 0 sen(π/6) sen(π/3) 1

a) Determine uma aproximação da velocidade e da aceleração nos 2 nós interioresusando diferenças finitas centrais.

b) Deduza uma estimativa para o espaçamento óptimo no cálculo da aceleraçãopor diferenças finitas centrais.

RESOLUÇÃO

a) Antes de mais, devemos observar que h = 1/3 e que os 2 pontos interiores sãot = 1/3 e t = 2/3.

Expressão para cálculo das velocidades por diferenças finitas centrais (p. 101, exp.(3.2.12)):

Dhf(x) =f(x + h)− f(x− h)

2h

Expressão para cálculo das acelerações por diferenças finitas centrais (p. 103, exp.(3.3.1)):

D2hf(x) =

f(x− h)− 2f(x) + f(x + h)h2

48 SEMANA 7

Concretizando para os valores dados na tabela e recorrendo à calculadora, obte-mos, sucessivamente:

Dhf(1/3) =f(1/3 + 1/3)− f(1/3− 1/3)

2× 1/3=

f(2/3)− f(0)2× 1/3

=sen(π/3)− 0

2× 1/3= 1.299

Dhf(2/3) =f(2/3 + 1/3)− f(2/3− 1/3)

2× 1/3=

f(1)− f(1/3)2× 1/3

=1− sen(π/6)

2× 1/3= 0.75

D2hf(1/3) =

f(1/3− 1/3)− 2f(1/3) + f(1/3 + 1/3)(1/3)2

=f(0)− 2f(1/3) + f(2/3)

(1/3)2=

0− 2sen(π/6) + sen(π/3)(1/3)2

= −1.2057

D2hf(2/3) =

f(2/3− 1/3)− 2f(2/3) + f(2/3 + 1/3)(1/3)2

=f(1/3)− 2f(2/3) + f(1)

(1/3)2=

sen(π/6)− 2sen(π/3) + 1(1/3)2

= −2.088457

b) Neste caso, o espaçamento h óptimo é desconhecido.

O valor exacto da segunda derivada f ′′(x) relaciona-se com o valor por diferençasfinitas centrais e o erro de aproximação, e′′2(x), inerente ao cálculo por este processo,do seguinte modo:

f ′′(x) =f(x− h)− 2f(h) + f(x + h)

h2− 1

12h2f (4)(η)

=f(x− h)− 2f(h) + f(x + h)

h2− e′′2(x)

Em representação em ponto flutuante, temos de contar ainda com os erros dearredondamento, e(x), no cálculo do valor da própria função, ou seja,

f(x) = f(x) + e(x) e, portanto

f ′′(x) =f(x− h)− 2f(h) + f(x + h)

h2

+e(x− h)− 2e(h) + e(x + h)

h2− 1

12h2f (4)(η)

=f(x− h)− 2f(h) + f(x + h)

h2+ E

onde

E =e(x− h)− 2e(h) + e(x + h)

h2− 1

12h2f (4)(η)


Considerando

∥∥∥f (4)∥∥∥∞

6 M4 e |e(x− h)− 2e(h) + e(x + h)| 6 4ε

onde M4 é o majorante das quartas derivadas e ε é um parâmetro que depende daforma como a função f é calculada, ou seja, é da ordem de grandeza da unidade dearredondamento do computador utilizado, podemos fazer

|E| 6 4ε

h2+

M4h2

12

O segundo membro é mínimo quando a sua primeira derivada, em ordem a h, fornula, isto é, quando

− 8ε

h3+

M4h

6= 0 ⇒ h =

(48ε

M4

)1/4

Portanto, o valor de h deduzido será a estimativa para o espaçamento óptimo nocálculo da aceleração por diferenças finitas centrais. ¥

Como complemento teórico à resolução deste problema, sugerimos a observaçãoatenta da Figura 3.5.1, na p. 108. do livro [Pina(1995)]. ¡


Ponto de inflexão

Obtenha o ponto de inflexão de uma função f no intervalo [0, 1] sendo conhecidos osseguintes valores:

x 0.00 0.25 0.50 0.75 1.00

f(x) 0.00 0.56 0.72 1.34 4.00

RESOLUÇÃOPodemos considerar os seguintes processos para resolver o problema:i) Determinar o polinómio interpolador e depois derivar analiticamente;ii) Determinar as derivadas aproximadas D2

hf(x) pela tabela e interpolar os valoresobtidos;

iii) Determinar os splines, seguido de derivação analítica.Em qualquer dos casos obtemos uma equação polinomial a solucionar. De notar

que existem outros processos, igualmente válidos para resolver este problema.

Processo i:Esquematicamente temos

pn(x) → p′′n(x) → p′′n(x) = 0

Assim, primeiro determinamos o polinómio interpolador p4(x) por diferenças di-vididas:

50 SEMANA 7

x y[·] y[·, ·] y[·, ·, ·] y[·, ·, ·, ·] y[·, ·, ·, ·, ·]0.00 0.00

2.24

0.25 0.56 −3.2

0.64 9.17(3)0.50 0.72 3.68 7.68

2.48 16.85(3)0.75 1.34 16.32

10.641.00 4.00

O polinómio é então

p(x) = 2.24x− 3.2x(x− 0.25) + 9.17(3)x(x− 0.25)(x− 0.50)

+ 7.68x(x− 0.25)(x− 0.50)(x− 0.75)

que, desenvolvido e agrupado na forma de potências simples de x corresponde a

p(x) = 3.4(6)x− 4.8x2 − 2.34(6)x3 + 7.68x4.

Derivando sucessivamente, obtemos

p′(x) = 3.4(6)− 9.6x− 7.04x2 + 30.72x3

p′′(x) = −9.6− 14.08x + 92.16x2

O ponto de inflexão é tal que

p′′(x) = 0 ⇔ x =−b±√b2 − 4ac

2aou seja, x = 0.408054 ∨ x = −0.255276

Portanto, o ponto de inflexão no intervalo [0, 1], obtido por este processo, éx ≈ 0.40805.

Processo ii:

Esquematicamente temos

D2hf(x) → p′′n(x) → p′′n(x) = 0

A segunda derivada é obtida por diferenças finitas centrais:

D2hf(x) =

f(x− h)− 2f(x) + f(x + h)h2

tal que h = 0.25. Assim, obtemos

x 0.00 0.25 0.50 0.75 1.00

y 0.00 0.56 0.72 1.34 4.00y′′ −6.4 7.36 32.64

e a correspondente tabela de diferenças divididas para determinar a interpolação deD2

hf(x):


x y′′[·] y′′[·, ·] y′′[·, ·, ·]0.25 −6.4

55.04

0.50 7.36 92.16

101.120.75 32.64

O polinómio que interpola a segunda derivada é, então

p′′(x) = −6.4 + 55.04(x− 0.25) + 92.16(x− 0.25)(x− 0.50)

que, desenvolvido e agrupado em potências de x corresponde a

p′′(x) = −8.64− 14.08x + 92.16x2


p′′(x) = 0 ⇔ x =−b±√b2 − 4ac

2aou seja, x = 0.391960 ∨ x = −0.239182


Processo iii:

Esquematicamente temos

Mi → S′′i (x) → S′′i (x) = 0

Reparar que não necessitamos de determinar o próprio spline cúbico Si(x), bas-tando, para o que pretendemos, calcular S′′i (x).

Dado que desconhecemos as derivadas y′ nos extremos x0 e x4, temos M0 = M4 =0, isto é, impomos S′′1 (x0) = 0 = M0 e S′′4 (x4) = 0 = M4.†

Para determinar M1, M3 e M3 faz-se

h

6Mi−1 +

2h

3Mi +

h

6Mi+1 =

yi+1 − 2yi + yi−1

hcom i = 1, 2, 3

12Mi−1 + 2Mi +

12Mi+1 =

3h2

(yi+1 − 2yi + yi−1) com i = 1, 2, 3

o que origina, na forma matricial,

2 1/2 01/2 2 1/20 1/2 2

M1

M2

M3

=

3h2

y2 − 2y1 + y0

y3 − 2y2 + y1

y4 − 2y3 + y2

=

−19.222.0897.92

†Como veremos, ao impor estas igualdades, os resultados deterioram-se.

52 SEMANA 7

Resolvendo o sistema de equações, por exemplo, através do método de Gauss esubstituição descendente, obtemos

M1

M2

M3

=

48.61711.3714−9.9428

Dado que S′′i = Mi, é de esperar que o ponto de inflexão esteja no segundo troço,pois M2 e M3 têm sinais diferentes.

Então, como a segunda derivada do i-ésimo troço de spline é tal que (Exp. (2.7.7),p. 81, [Pina(1995)])

S′′i (x) = Mi−1xi − x

h+ Mi

x− xi−1

h

obtemos para o segundo troço, isto é, para o subintervalo [0.25, 0.5]

S′′2 (x) = M1x2 − x

h+ M2

x− x1

h

= −9.94280.50− x

0.25+ 1.3714

x− 0.250.25


S′′2 (x) = 0 ⇔ −9.94280.50− x

0.25+ 1.3714

x− 0.250.25

= 0 ⇔ x = 0.469697.


Comparação entre os três processos:Observando as Figuras 7.4.1(a) e 7.4.1(b), que mostram o polinómio obtido pelo

processo i), é possível concluirmos que o ponto de inflexão positivo se encontra navizinhança de 0.4. No entanto, existe um outro ponto de inflexão negativo, perto de0.25.

−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1−3

−2

−1

0

1

2

3

4

5

(a)0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0

0.5

1

1.5

2

2.5

3

3.5

4

4.5

(b)

Figura 7.4.1: Polinómio de quarta ordem obtido pelo processo i

Os valores do ponto de inflexão obtidos pelos processos i e ii são bastante seme-lhantes, pois os polinómios de grau 2 obtidos são quase coincidentes (Figura 7.4.2).


O resultado com o processo iii não será o melhor, dado que impusemos um va-lor nulo às segundas derivadas nas extremidades do intervalo (S′′i (0) = 0 = M0 eS′′i (1) = 0 = M4).

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1−20

−10

0

10

20

30

40

50

60

70

Processo i

Processo ii

Processo iii

Figura 7.4.2: Polinómios obtidos por derivação analítica (Processos i e ii) e porspline cúbico natural (Processo iii) )

A título comparativo e para reflexão , mostramos o polinómio obtido pelo processoi e o spline cúbico natural na Figura 7.4.3.† Porque se verificam grandes discrepânciasnos intervalos [0, 0.25] e [0.75, 1]?

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 10

0.5

1

1.5

2

2.5

3

3.5

4

Processo iii

Processo i

Figura 7.4.3: Polinómios de quarta ordem (Processo i) e spline cúbico (Processo iii)

¥†Relembramos que não é necessário construir o spline para calcular o ponto de inflexão.

54 SEMANA 7


Espaçamento desigual

Dados 3 pontos, (x1, y1), (x2, y2), (x3, y3), com espaçamento desigual entre as suasabcissas, deduza uma fórmula para calcular uma aproximação da segunda derivadanum ponto qualquer do intervalo [x1, x3]. Considerando os pontos (1, 1), (2, 4), (5, 5),utilize a fórmula para calcular y′′(2) e y′′(3).

Em qual dos pontos, x2 ou (x1 + x3)/2, é de esperar um erro absoluto menor?Justifique (admita que as derivadas de y = f(x) se mantêm na mesma ordem degrandeza em [x1, x3]).

RESOLUÇÃO

Pretendemos deduzir uma fórmula para calcular D2hf ≈ f ′′(x) = y′′.

De entre as várias possibilidades, a dedução da diferença finita com espaçamentodesigual é a mais simples. De notar que o recurso a splines não é o mais adequado, poisnão se conhece a função e estes requerem o conhecimento de m0 (splines quadráticos)ou M0 e Mn (splines cúbicos). Assim,

D2h = p′′2(x) = 2f [x1, x2, x3] = 2

f [x1, x2]− f [x2, x3]x1 − x3

= 2f(x1)−f(x2)

x1−x2− f(x2)−f(x3)

x2−x3

x1 − x3

Como D2h não depende de x, temos

f ′′(2) ≡ f ′′(3) ≈ 21−41−2 − 4−5

2−5

1− 5= −4

3

A expressão do erro de D2h é

e′′2 = f [x1, x2, x3, x, x, x] W2(x)

+ 2f [x1, x2, x3, x, x]W ′2(x)

+ f [x1, x2, x3, x] W ′′2 (x)

onde, usando

f [x1, x2, x3, . . . , xk] =f (k)(ξ)

k!

vem

e′′2 =f (5)(r)

120W2(x)

+f (4)(ξ)

12W ′

2(x)

+f (3)(η)

6W ′′

2 (x)


Como as derivadas mantêm a mesma ordem de grandeza, ficamos com

e′′2 6 M

12

(110|W2(x)|+ |W ′

2(x)|+ 2|W ′′2 (x)|

)

onde

W2 = (x− x1)(x− x2)(x− x3) = (x− 1)(x− 2)(x− 5)

W ′2 = (x− x2)(x− x3) + (x− x1)(x− x3) + (x− x1)(x− x2)

W ′′2 = 2(x− x3) + 2(x− x2) + 2(x− x1) = 6x− 16

Compilando os valores numa tabela, obtemos

x |W2(x)| |W ′2(x)| |W ′′

2 (x)| e′′2x = x2 = 2 0 3 4 11

12M

x = (x1 + x3)/2 = 3 4 4 2 8.412 M

Concluímos então que é de esperar um erro absoluto menor em x, embora emtermos de majorante a diferença encontrada não seja significativa. ¥

8

TÓPICOS: Integração Numérica: Regras de Newton-Cotes simples e com-postas; Regra de Gauss-Legendre-Lobatto; Regras de Gauss-Legendre e do trapéziocomposta. Erros absoluto e relativo. Estimativa e majorante do erro.


8.1 INTEGRAÇÃO NUMÉRICA:

Regras do trapézio simples e de Simpson simples

e composta

(a) Calcule, pela regra do trapézio simples e pela regra de Simpson simples, o valoraproximado do integral

I =∫ 3

2

exp (1 + cos x)dx.

(b) Idem pela regra de Simpson composta com 2 subintervalos.

(c) Estime o erro absoluto cometido na alínea anterior.

RESOLUÇÃO

(a) As regras referidas correspondem, respectivamente, às expressões (4.2.6) e(4.2.7), p. 120, de [Pina(1995)]:

TIh(f) =b− a

2[f(a) + f(b)]

SIh(f) =b− a

6

[f(a) + 4f(

a + b

2) + f(b)

]

onde a e b são os limites de integração.

Concretizado para a função f(x) = exp (1 + cos x), com a = 2 e b = 3 obtemos

TIh(f) =3− 2

2[f(2) + f(3)] = 1.401495675

SIh(f) =3− 2

6

[f(2) + 4f(

2 + 32

) + f(3)]

= 1.280503052

(b)

58 SEMANA 8

Aplicação directa da exp. (4.5.10): A exp. para o cálculo com a regra deSimpson composta com N subintervalos é (Exp. (4.5.10), p. 138, de [Pina(1995)]):

ScIh(f) =h

6

[f(a) + f(b) + 2

N−1∑

i=1

f(ai) + 4N∑

i=1

f(ai−1 + h/2)

]

onde h = (b− a)/N .

No caso presente, como N = 2 teremos

ScIh(f) =h

6[f(a) + f(b) + 2f(a1) + 4(f(a0 + h/2) + f(a1 + h/2))]

com a = 2, b = 3, h = (3−2)/2 = 0.5, a0 = 2 = a, a1 = a0 +h = 2.5, a2 = a1 +h = b.

Assim, vem, sucessivamente

ScIh(f) =0.56f(2) + f(3) + 2f(2.5) + 4[f(2 + 0.5/2) + f(2.5 + 0.5/2)]

=0.56f(2) + f(3) + 2f(2.5) + 4[f(2.25) + f(2.75)]

= 1.279922906

Resolução alternativa e justificação da exp. (4.5.10): Neste caso conside-ramos 2 intervalos, usamos a regra de Simpson simples em cada um deles e somamosos valores obtidos, pois sabemos que

I =∫ b

a

f(x)dx =∫ a1

a

f(x)dx +∫ b

a1

f(x)dx

=∫ a1

a0

f(x)dx +∫ a2

a1

f(x)dx =∫ 2.5

2

f(x)dx +∫ 3

2.5

f(x)dx.

Portanto, aplicando a regra de Simpson simples a cada um dos integrais acima,obtemos

ScIh(f) =2.5− 2

6[f(2) + 4f(2.25) + f(2.5)]

+3− 2.5

6[f(2.5) + 4f(2.75) + f(3)] = 1.279922906

(c) Antes de mais, há que notar que se pretende uma estimativa, pois desconhe-cemos o valor exacto do integral.

Os erros de integração das regras de Simpson simples e composta são dados, res-pectivamente pelas expressões (4.2.18), p. 124 e (4.5.11), p. 138, de [Pina(1995)]:

SEh(f) = − 12880

f (4)(ξ)(b− a)5 = I − SIh(f) (8.1.1)

ScEh(f) = −b− a

2880f (4)(ξ)h4 = I − ScIh(f) onde h =

b− a

N(8.1.2)

A exp. (8.1.2) pode escrever-se da seguinte forma:

ScEh(f) = −b− a

2880f (4)(ξ)

(b− a

N

)4

= − 1N4

12880

f (4)(ξ) (b− a)5 (8.1.3)


pelo que, e como N = 2, fica

I − SIh(f) = − 12880

f (4)(ξ)(b− a)5 = −c (8.1.4)

I − ScIh(f) = − 124

12880

f (4)(ξ) (b− a)5 = − 116

c (8.1.5)

Subtraindo (4) a (5), membro a membro, fica

I − SIh(f)− I + ScIh(f) = −c +124

c ⇔ ScIh(f)− SIh(f) =(

116− 1

)c

(8.1.6)

ou seja,

c =(

116− 1

)−1 [ScIh(f)− SIh(f)

]=

(−15

16

)−1 [ScIh(f)− SIh(f)

]

= −1615

[ScIh(f)− SIh(f)

](8.1.7)

Substituindo c em (5), obtemos

I − ScIh(f) = − 116

(−16

15

) [ScIh(f)− SIh(f)

]=

ScIh(f)− SIh(f)15

(8.1.8)

Então, substituindo os valores calculados nas alíneas anteriores, obtemos umaestimativa de erro absoluto cometido na alínea b) de 3.9× 10−5.† ¥

A Figura 8.1.1 mostra a negro a diferença entre as áreas abaixo da curva da funçãof(x) = exp(1+cos(x)) e dos polinómios de grau 1 (Figura 8.1.1(a): Regra do trapéziosimples) e grau 2 (Figura 8.1.1(b): Regra de Simpson simples). É notório o melhordesempenho da regra de Simpson que, recordamos, é de ordem 3.

2 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 30

0.5

1

1.5

2

2.5

(a) Regra do trapézio simples2 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3

0

0.5

1

1.5

2

2.5

(b) Regra de Simpson simples

Figura 8.1.1: Diferenças entre integração exacta e com regras do trapézio e Simpsonsimples

¡

†Admitimos que a estimativa de f (4) é válida em ambos os casos, sendo o máximo no intervalo[2, 3].

60 SEMANA 8


Regra de Gauss-Legendre e de Gauss-Legendre-

Lobatto

Pretende-se calcular o seguinte integral

I =∫ 2

0

sinh(x)dx.

(a) Obtenha uma aproximação com 2 pontos de Gauss-Legendre.

(b) Idem, com 3 pontos de Gauss-Legendre-Lobatto.

(c) Calcule o erro absoluto e relativo cometido em cada caso.

RESOLUÇÃO

(a) Mudança de coordenadas (exp. (4.1.2), p. 116):

T (ξ) =a(1− ξ)

2+

b(1 + ξ)2

=0(1− ξ)

2+

2(1 + ξ)2

= 1 + ξ

J(ξ) =b− a

2=

22

= 1

Então,

I =∫ 2

0

sinh(x)dx =∫ 1

−1

sinh(1 + ξ)× 1dξ =∫ 1

−1

sinh(1 + ξ)dξ.

Com 2 pontos, temos as abcissas e os pesos (Tabela 4.4.1, p. 132)

ξ1 = −0.5773502692, A1 = 1,

ξ1 = +0.5773502692, A2 = 1.

e, portanto

I =∫ 2

0

sinh(x)dx ≈ A1f(ξ1) + A2f(ξ2) = 0.4353457822 + 2.317793457

= 2.753139239

(b) As regras de Gauss-Lobatto são tais que possuem os dois pontos dos extremosdo intervalo (p. 135, de [Pina(1995)]) e os restantes no interior:

Ih(f) = Af(a) + Bf(b) +n∑

i=1

Aif(xi)

Para n = 3 obtemos a regra de Simpson (ver Problema 4.12.11, p. 158, [Pina(1995)]):

Ih(f) =b− a

6

[f(a) + 4f(

a + b

2) + f(b)

]ou seja


I =∫ 2

0

sinh(x)dx ≈ 2− 06

[f(0) + 4f(1) + f(2)]

=13(0 + 4× 1.175201194 + 3.626860408) = 2.775888395

(c) O valor exacto do integral é

I =∫ 2

0

sinh(x)dx = cosh(x)|20 = 2.762195691 pelo que

Alínea a)

E = I(f)− Ih(f) = +0.009056452

e =E

I(f)= +3.2787× 10−3

Alínea b)

E = I(f)− Ih(f) = −0.013692704

e =E

I(f)= −4.9571× 10−3

¥


Regras de Gauss-Legendre e do trapézio com-

posta

Pretende-se calcular o seguinte integral

I =∫ 2

1

ln(x)dx.

(a) Calcule uma aproximação pela regra de Gauss-Legendre com 2 pontos.(b) Calcule outra aproximação pela regra do trapézio composta usando 5 valores

da função integranda e um espaçamento uniforme.(c) Calcule um majorante do erro em cada caso. Obtenha também os erros abso-

luto e relativo cometidos em cada caso.

RESOLUÇÃO(a) Mudança de coordenadas (exp. (4.1.2), p. 116):

T (ξ) =a(1− ξ)

2+

b(1 + ξ)2

=1(1− ξ)

2+

2(1 + ξ)2

=12(3 + ξ)

J(ξ) =b− a

2=

12

Então,

I =∫ 2

1

ln(x)dx =∫ 1

−1

ln[12(3 + ξ)

]× 1

2dξ =

12

∫ 1

−1

ln[12(3 + ξ)

]dξ.

62 SEMANA 8

Com 2 pontos, temos as abcissas e os pesos

ξ1 = −√

1/3, A1 = 1,

ξ2 = +√

1/3, A2 = 1.

e, portanto

I =∫ 2

1

ln(x)dx ≈ A1f(ξ1) + A2f(ξ2)

=12

ln

[12(3−

√1/3)

]+ ln

[12(3 +

√1/3)

]= 0.3865949441

(b) Considerando 5 valores da função e um espaçamento uniforme, temos

| — | — | — | — |1.00 1.25 1.50 1.75 2.00

sendo h = 1/4 = 0.25.Concretizando,

Ih(f) = h

[ln(1.00)

2+

ln(2.00)2

+ ln (1.25) + ln (1.50) + ln (1.75)]

= 0.25[0.00 +

ln(2.00)2

+ ln (1.25× 1.50× 1.75)]

= 0.3836995094

(c)Um majorante do erro:Alínea a)Atendendo às expressões (4.4.9) e (4.4.10), p. 130, de [Pina(1995)], obtemos para

a regra de Gauss-Legendre com 2 pontos (n = 2):

|E| 6 14320

(2− 1)2×2+1∥∥∥f (2×2)

∥∥∥[1,2]

∞=

14320

(2− 1)2×2+1 maxx∈[1,2]

∣∣∣∣−61x4

∣∣∣∣

=1

4320(2− 1)2×2+1 × 6 = 0.1388888889× 10−2

Alínea b)Atendendo à expressão (4.5.9), p. 137, de [Pina(1995)], obtemos para a regra do

trapézio composta usando 5 valores da função (h = 1/4):

|E| 6 b− a

12‖f ′′‖[1,2]

∞ h2 =2− 112

maxx∈[1,2]

∣∣∣∣−1x2

∣∣∣∣×(

14

)2

=2− 112

× 1× 142

= 0.5208333333× 10−2

Erros absolutos e relativo:O valor exacto do integral é

I =∫ 2

0

ln(x)dx = x ln(x)− x|21 = 0.386294361 pelo que


Alínea a)

E = I(f)− Ih(f) = −0.0003005831

e =E

I(f)= −0.0007781193058

Alínea b)

E = I(f)− Ih(f) = +0.0025948516

e =E

I(f)= +0.006717290911

¥

9

TÓPICOS: Integração Numérica (CONT.): Dedução e grau de regras deintegração; Regra do trapézio corrigida; Regra de Simpson adaptativa iterativa.



Dedução e grau de regras de integração

Pretende-se deduzir uma regra de integração do tipo

I(f) =∫ +1

−1

sinh(x)f(x)dx ≈ Ih(f) = A1[f(−1) + f(+1)] + A2[f(−ξ) + f(+ξ)]

a) Calcule os pesos A1 e A2 de modo a que a regra tenha o maior grau de exactidãopossível para ξ =

√13 .

b) Que polinómios são integrados exactamente por esta regra?

c) Caracterize esta regra quanto à família, ao número de pontos usados, à estima-tiva de erro e ao grau de exactidão da regra justificando a resposta.

RESOLUÇÃO

a) Como a regra é referida a um intervalo simétrico em relação à origem , todosos integrais do tipo,:

Im(f) =∫ +1

−1

xmdx,

a que se dá o nome de momentos, com m ímpar anulam-se. Assim sendo, a regra deintegração terá de integrar exactamente os dois primeiros momentos de ordem par,ou seja,

I0(f) =∫ +1

−1

x0dx = 2 e I2(f) =∫ +1

−1

x2dx =23.

Para estabelecer as duas equações que determinam os pesos A1 e A2, temos deobrigar a regra a um cálculo exacto das funções f(x) = 1 e f(x) = x2. Substituindo,obtemos o seguinte sistema de equações

66 SEMANA 9

2A1 + 2A2 = 2

2A1 + 23A2 = 2

3

A solução deste sistema é A1 = 0 e A2 = 1.

b) Como os momentos ímpares são todos integrados exactamente devido à dispo-sição simétrica dos pontos, é de esperar que pelo menos a regra integre exactamenteas funções 1, x, x2 e x3. Ou seja, para estabelecer que o grau de exactidão da regra é3 há que comprovar que a função x4 não é integrada exactamente. Com efeito, o valorexacto é I4 = 2

5 enquanto que o valor calculado pela regra é Ih(f) = 29 6= I(f) = 2

5 .

Então, são integrados exactamente todos os polinómios de grau ≤ 3, pelo que aregra é de grau de exactidão 3.

c) Como A1 = 0, a contribuição dos pontos nos extremos do intervalo é nula, peloque só há dois pontos interiores em ξ = ±

√13 .

A regra obtida corresponde à regra de Gauss-Legendre com 2 pontos a qual temum grau de exactidão de 3.

A estimativa de erro é dada pelas expressões (4.4.9) e (4.4.10) em [Pina(1995)], p.130, com n = 2 e b− a = 2.

¥


Regra do trapézio corrigida

a) Calcular o integral I(f) =∫ 1

0f(x)dx com f(x) = ln

(1 + x2

)pela regra do trapézio

corrigida.

b) Obtenha um majorante para o erro cometido.

Nota: f4(x) = 12(6x2 − x4 − 1

)/

(1 + x2

)4.

c) Há, neste caso, alguma vantagem particular em usar esta regra?

RESOLUÇÃO

a) A expressão desta regra é

Ih(f) =b− a

2[f(a) + f(b)] +

(b− a)2

12[f ′(a)− f ′(b)]

Concretizando para o caso presente, isto é,

a = 0, b = 1, f(0) = 0, f(1) = 0.6931471806,

f ′(x) =2x

1 + x2, f ′(0) = 0, f ′(1) = 1.

obtemos

Ih(f) =1− 0

2[0 + 0.6931471806] +

(1− 0)2

12[0− 1] = 0.263240257


b) O erro é tal que

Eh(f) 6 (b− a)5

720f (4)(ξ)

sendo o majorante dado por

|Eh(f)| 6 (b− a)5

720

∥∥∥f (4)∥∥∥

[0,1]

∞=

(b− a)5

720max

x∈[0,1]

∣∣∣f (4)∣∣∣

Determinação do majorante:

Os valores de f (4)(x) nos extremos do intervalo são:

f (4)(0) = −12 e f (4)(1) = 3.

O ponto intermédio é tal que f (5)(x) = 0, sendo

f (5)(x) =12(12x− 4x3)(1 + x2)4 − 12(6x2 − x4 − 1)× 4(1 + x2)3 × 2x

(1 + x2)8

=48(3x− x3)(1 + x2)4 − 48(6x2 − x4 − 1)× (1 + x2)3 × 2x

(1 + x2)8

=48[(3x− x3)(1 + x2)− (6x2 − x4 − 1)× 2x]

(1 + x2)5

=48(x5 − 10x3 + 5x)

(1 + x2)5=

48x(x4 − 10x2 + 5)(1 + x2)5

Então, vem

f (5)(x) = 0 ⇒ z2 − 10z + 5 = 0

⇔ z =−b±√b2 − 4ac

2a⇔ z = 9.472135955 ∨ z = 0.5278640450

ou seja,

f (5)(x) = 0 ⇔ x = ±3.077683537 ∨ x = ±0.7265425280

O ponto de estacionaridade no intervalo [0, 1] é x = 0.7265425280, sendo

f (4)(0.7265425280) = 4.158813728.

Contudo, este não é o máximo em valor absoluto da função f (4)(x) para x ∈ [0, 1],mas sim

f (4)(0) = 12.

Portanto, o majorante do erro é

|Eh(f)| 6 (1− 0)5

720× 12 = 0.0166666

68 SEMANA 9

Na Figura 9.2.1 podemos ver graficamente a quarta derivada.

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1−12

−10

−8

−6

−4

−2

0

2

4

6

Figura 9.2.1: f4(x) = 12(6x2 − x4 − 1

)/

(1 + x2

)4 para x ∈ [0, 1]

c) Neste caso, e como a função é tal que f(x) ∈ C4(Ω), a regra do trapézio corrigidatem como erro (exp. (4.5.13), p. 138, de [Pina(1995)]):

Eh(f) =b− a

720f (4)(ξ)h4

dependendo de h à quarta e não ao quadrado como na regra do trapézio simples (exp.(4.5.9), p. 138, de [Pina(1995)]):

Eh(f) = −b− a

12f ′′(ξ)h2

Só não haverá vantagens quando f ′(a) = f ′(b), pois neste caso a regra do trapéziocorrigida coincide com a regra do trapézio simples. ¥


Regra de Simpson adaptativa iterativa

Use uma regra de Simpson adaptativa iterativa para aproximar o integral

I =∫ 1

0

√x dx

com as tolerâncias de erro total ε = 0.0025 e ε = 0.0002.

CONCEITOS TEÓRICOS

O valor de um integral num dado troço [xi, xi+h] de comprimento h pode seraproximado por, Ih,

| — × — |xi xi + h/2 xi + h


Ih =h

6[f(xi) + 4f(xi + h/2) + f(xi + h)] (9.3.1)

ou 2 subintervalos, [xi, xi+h/2] e [xi+h/2, xi+h], cada um com comprimento h/2, Ih:

| — × — | — × — |xi xi + h/4 xi + h/2 xi + 3h/2 xi + h

Ih =h/26

[f(xi) + 4f(xi + h/4) + 2f(xi + h/2) + 4f(xi + 3h/4) + f(xi + h)]

=h

12[f(xi) + 4f(xi + h/4) + 2f(xi + h/2) + 4f(xi + 3h/4) + f(xi + h)]

(9.3.2)

Uma estimativa do erro para a integração num subintervalo de comprimento h édada por†

E = I − Ih ≈ 115

(Ih − Ih

)

Considerando que cada troço contribui para o erro total, ε, com um erro proporci-onal ao seu comprimento (ler segundo parágrafo na p. 145 e enunciado do Problema4.12.25, p. 160, de [Pina(1995)]), teremos

E = I − Ih ≈ 115

(Ih − Ih

)6 ε

h

b− a(9.3.3)

onde a e b são os limites de integração de todo o integral.

Como complemento a estes Conceitos Teóricos, remetemos o leitor para as páginas144 e 145 de [Pina(1995)].

RESOLUÇÃO

A Figura 9.3.1 representa graficamente a função f(x) =√

x no intervalo [0, 1].Observamos que o troço [1/2, 1] apresenta menor variação da função, pelo que o es-colhemos como primeiro subintervalo a analisar. Se iniciássemos o cálculo pelo troço[0, 1/2] teríamos mais trabalho. Uma implementação computacional calcularia as es-timativas de erro para saber onde começar.

†Ver resolução do Exercício 8.1, em particular a exp. (8.1.8), p. 59.

70 SEMANA 9

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 10

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

Elevada variacao em f(x)

Pequena variacao em f(x)

Figura 9.3.1: f(x) =√

x para x ∈ [0, 1]

• Troço [1/2,1]:Neste caso temos h = 1/2.

| — × — | — × — |1/2 5/8 3/4 7/8 1

1 subintervalo: Ih1[1/2,1] =1/26

(√1/2 + 4

√3/4 +

√1)

= 0.43093403302703

2 subintervalos: Ih2[1/2,1] =1/212

(√1/2 + 4

√5/8 + 2

√3/4 + 4

√7/8 +

√1)

= 0.43096219315407

E(ε=0.0025)[1/2,1] =

Ih2[1/2,1] − Ih1[1/2,1]

15= 1.877341803169230× 10−6

<1/2

1− 0× 0.0025 =

0.00252

= 0.00125 = 1.25× 10−3

E(ε=0.0002)[1/2,1] =

Ih2[1/2,1] − Ih1[1/2,1]

15= 1.877341803169230× 10−6

<1/2

1− 0× 0.0002 =

0.00022

= 0.0001 = 1.00× 10−4

Ambos os critérios de erro são satisfeitos para este troço, pelo que passamos parao troço [0, 1/2].

• Troço [0,1/2]:Também neste caso temos h = 1/2.

| — × — | — × — |0 1/8 1/4 3/8 1/2


1 subintervalo: Ih1[0,1/2] =1/26

(√0 + 4

√1/4 +

√1/2

)

= 0.22559223176555

2 subintervalos: Ih2[0,1/2] =1/212

(√0 + 4

√1/8 + 2

√1/4 + 4

√3/8 +

√1/2

)

= 0.23211708693095

E(ε=0.0025)[0,1/2] =

Ih2[0,1/2] − Ih1[0,1/2]

15= 4.349903443603494× 10−4

<1/2

1− 0× 0.0025 = 0.00125 = 1.25× 10−3

E(ε=0.0002)[0,1/2] =

Ih2[0,1/2] − Ih1[0,1/2]

15= 4.349903443603494× 10−4

>1/2

1− 0× 0.0002 = 0.0001 = 1.00× 10−4

O critério de erro ε = 0.0025 é satisfeito para este troço, mas não o critérioε = 0.0002.

Para este último caso temos de subdividir o intervalo [0, 1/2]. Ficaremos, então,com dois novos troços: [1/4, 1/2] e [0, 1/4].

Troço [1/4, 1/2]:Agora temos h = 1/4.

| — × — | — × — |1/4 5/16 3/8 7/16 1/2

1 subintervalo: Ih1[1/4,1/2] =1/46

(√1/4 + 4

√3/8 +

√1/2

)

= 0.15235818849874

2 subintervalos: Ih2[1/4,1/2] =1/412

(√1/4 + 4

√5/16 + 2

√3/8 + 4

√7/16 +

√1/2

)

= 0.15236814460714

E(ε=0.0002)[1/4,1/2] =

Ih2[1/4,1/2] − Ih1[1/4,1/2]

15= 6.637405598142187× 10−7

<1/4

1− 0× 0.0002 = 0.00005 = 5.00× 10−5

Troço [0, 1/4]:À semelhança do troço [1/4, 1/2] temos também h = 1/4.

72 SEMANA 9

| — × — | — × — |0 1/16 1/8 3/16 1/4


(√0 + 4

√1/8 +

√1/4

)

= 0.07975889843221


(√0 + 4

√1/16 + 2

√1/8 + 4

√3/16 +

√1/4

)

= 0.08206578309907

E(ε=0.0002)[0,1/4] =

Ih2[0,1/4] − Ih1[0,1/4]

15= 1.537923111239366× 10−4

>1/4

1− 0× 0.0002 = 0.00005 = 5.00× 10−4

Como vemos, para a tolerância ε = 0.0002, é necessário subdividir o troço [0, 1/4]nos troços [1/8, 1/4] e [0, 1/8]. Em ambos os casos temos h = 1/8.

Troço [1/8, 1/4]:

| — × — | — × — |1/8 5/32 3/16 7/32 1/4

1 subintervalo: Ih1[1/8,1/4] =1/86

(√1/8 + 4

√3/16 +

√1/4

)

= 0.05386675412838

2 subintervalos: Ih2[1/8,1/4] =1/812

(√1/8 + 4

√5/32 + 2

√3/16 + 4

√7/32 +

√1/4

)

= 0.05387027414426

E(ε=0.0002)[0,1/4] =

Ih2[0,1/4] − Ih1[0,1/4]

15= 2.346677253961538× 10−7

<1/8

1− 0× 0.0002 = 0.000025 = 2.50× 10−5

Troço [0, 1/8]:

| — × — | — × — |0 1/32 1/16 3/32 1/8



(√0 + 4

√1/16 +

√1/8

)

= 0.02819902897069


(√0 + 4

√1/32 + 2

√1/16 + 4

√3/32 +

√1/8

)

= 0.02901463586637

E(ε=0.0002)[0,1/8] =

Ih2[0,1/8] − Ih1[0,1/8]

15= 5.437379304504368× 10−5

>1/8

1− 0× 0.0002 = 0.000025 = 2.50× 10−5

Verificamos que é ainda necessário subdividir este troço em dois e começamos asuspeitar que existe algures um problema na resolução deste exercício.

A aproximação do integral é, nesta iteração e para o critério ε = 0.0002,

Ih = Ih2[1/2,1] + Ih2[1/4,1/2]

+ Ih2[1/8,1/4] + Ih2[0,1/8]

= 0.43096219315407 + 0.15236814460714

+ 0.05387027414426 + 0.02901463586637

= 0.66621524777184

O valor exacto do integral é 2/3.Reflectindo um pouco, notamos que a estimativa do erro utilizada não tem suporte

quando a derivada envolvida não é limitada, como acontece para x = 0 neste problema.Assim, no cálculo do integral dado existem problemas de convergência. Estes pro-

blemas também se encontram nos actuais programas comerciais como, por exemplo,na função QUAD do MATLAB que efectua a quadratura de Simpson adaptativa.

Para verificar o que atrás foi dito, convidamos o leitor a emitir os comandos

f = @(x)sqrt(x); (f(x) =√

x)a = 0; b = 1; (limites de integração)tolerancia_do_erro = 0.0002; (ε = 0.0002)I_S_adapt = quad(f,a,b,tolerancia_do_erro); (valor numérico)I_exacto = 2/3; (valor exacto)E = I_exacto - I_S_adapt; (erro absoluto)

no MATLAB e a observar os resultados.Um utilizador menos avisado pode ver-se na situação de o resultado fornecido não

cumprir a tolerância exigida, pois o MATLAB não o avisa de tal. ¥

10

TÓPICOS: Equações Não-Lineares: Métodos da Bissecção, Falsa Posição eSecante; Método da Bissecção e zeros múltiplos; Método da Falsa Posição.


10.1 DETERMINAÇÃODE ZEROS DE EQUAÇÕES

NÃO-LINEARES:

Métodos da Bissecção, Falsa Posição e Secante

Verifique que a função f(x) = x3−2 exp(−x) tem um zero no intervalo [0, 1]. Calculeeste zero com 3 dígitos decimais correctos utilizando os métodos: i) da Bissecção, ii)da Falsa Posição e iii) da Secante.

RESOLUÇÃO

Pelo teorema do valor intermédio (p. 315 do livro [Ferreira(1985)]), sendo f(x)uma função contínua com mudança de sinal no valor da função nos pontos extremosdo intervalo [0, 1], então entre estes existe um ponto z ∈ [0, 1] : f(z) = 0.

Neste caso mostra-se que:

f(x) = x3 − 2 exp(−x) ⇒

f(0) = −2

f(1) ≈ 0.26421

ou seja,

f(0)× f(1) < 0,

i.e., a função apresenta pelo menos um zero no intervalo. Sendo f(x) monótonacrescente, só pode ter um zero.

i) Método da Bisseção (Ordem de convergência 1):

Há 3 etapas a considerar na determinação do zero:

1. Aproximação inicial ao zero.

Considere-se um intervalo [a, b] tal que sendo f(x) uma função contínua, verifica-seobrigatoriamente f(a)× f(b) < 0.

76 SEMANA 10

2. Processo iterativo: Começar com o intervalo [a, b] = [a0, b0] iterando daseguinte forma:

xk+1 =ak + bk

2→

f(ak)× f(xk+1) < 0 ⇒ ak+1 = ak, bk+1 = xk+1

f(ak)× f(xk+1) > 0 ⇒ ak+1 = xk+1, bk+1 = bk

O processo consiste em subdivisão sucessiva do intervalo em dois e escolha de umdeles.

3. Critério de paragem:Se |ak − bk| < ε, parar.O comprimento total do último intervalo escolhido é na pior das situações a medida

de erro na aproximação ao zero. Por isso diz-se que mede a incerteza na localizaçãodo zero.

É possível neste caso saber a priori o número de iterações (exp. (5.2.2), [Pina(1995)])necessário para garantir que o erro entre a aproximação e o zero exacto é menor queum determinado valor de desvio ε. Esse número de divisões pode ser calculado combase no comprimento do intervalo na última bissecção da seguinte forma:

|ek| ≤ |a− b|2k

,

ou seja, expressando o critério de paragem em termos do número de iterações neces-sárias, vem

|en| ≤ |a− b|2n

< ε ⇒ |a− b|ε

< 2n ⇔ n log 2 > log( |a− b|

ε

)

⇔ n >log

(|a−b|

ε

)

log 2.

Pretendemos 3 dígitos decimais exactos no intervalo [a0, b0] = [0, 1] pelo queε = 0.001 = 10−3. Assim, obtemos

n >log

(|a−b|

ε

)

log 2=

log(|1−0|10−3

)

log 2= 9.97 ⇔ n > 10.

A seguinte tabela apresenta os resultados em cada iteração.

k ak f(ak) bk f(bk) xk+1 f(xk+1)

0 0 −2 1 +0.2642 0.5 −1.088

1 0.5 −1.088 1 +0.2642 0.75 −0.5229

2 0.75 −0.5229 1 +0.2642 0.875 −0.1638

3 0.875 −0.1638 1 +0.2642 0.9375 +(.4076)10−1

4 0.875 −0.1638 0.9375 +(.4076)10−1 0.90625 −(.6378)10−1

5 0.90625 −(.6378)10−1 0.9375 +(.4076)10−1 0.921875 −(.1209)10−1

6 0.921875 −(.1209)10−1 0.9375 +(.4076)10−1 0.929688 +(.1419)10−1

7 0.921875 −(.1209)10−1 0.929688 +(.1419)10−1 0.925781 +(.1017)10−2

8 0.921875 −(.1209)10−1 0.925781 +(.1017)10−2 0.923828 −(.5544)10−2

9 0.923828 −(.5544)10−2 0.925781 +(.1017)10−2 0.924805 −(.2266)10−2

10 0.924805 −(.2266)10−2 0.925781 +(.1017)10−2 0.925293 −(.6252)10−3


A aproximação ao zero obtida pelo método da Bissecção é z ≈ 0.925293.

ii) Método da Falsa Posição (Ordem de convergência 1 para zeros simples):


Considere-se um intervalo [a, b], tal que sendo f(x) uma função contínua, verifica-se obrigatoriamente f(a)× f(b) < 0.

2. Processo iterativo:

Começar com o intervalo [a, b]=[a0, b0] iterando da seguinte forma:

xk+1 =akf(bk)− bkf(ak)

f(bk)− f(ak)

f(ak)× f(xk+1) < 0 ⇒ ak+1 = ak, bk+1 = xk+1

f(ak)× f(xk+1) > 0 ⇒ ak+1 = xk+1, bk+1 = bk

3. Critério de paragem:

Neste caso utiliza-se um critério universal baseado na série de Taylor. Numa vizi-nhança suficientemente pequena do zero pode considerar-se a seguinte aproximação

f(xk+1) ∼= f(z) + f ′(z)× (xk+1 − z)1!

.

Logo,

|f(xn)||f ′(x)|

∼= |(xn − z)| = |en| 6 ε.

Sendo m um minorante de f ′(x) no intervalo, tem-se

|f(xn)| 6 mε.

Por outro lado sendo M um majorante de f ′(x) no intervalo, tem-se

|f(xn)|M

6 |en| 6 |f(xn)|m

M |z − xn| 6 |f(xn)| 6 m |z − xn| ,

Assim transforma-se um critério de paragem definido para as abcissas (mas cujoz é desconhecido), num definido para as ordenadas onde se conhece f(xn).

|f(xn)| 6 mε.

Este é o critério de paragem universal que se vai utilizar.

Neste problema a tolerância requerida é ε = 10−3 pois o intervalo onde está o zeroz ∈ [0, 1].

Cálculo do minorante m:

78 SEMANA 10

O valor de m minorante de f ′(x) no intervalo é obtido estudando f ′(x) no intervalo,sendo

f(x) = x3 − 2 exp(−x),

f ′(x) = 3x2 + 2 exp(−x) e

f ′′(x) = 6x− 2 exp(−x).

Podemos observar que no intervalo [0, 1] a derivada f ′(x) será primeiro decrescente(até aproximadamente x = 0.26 e depois crescente. Uma forma expedita de estimarum minorante e um majorante para f ′(x) consiste em considerar a pior situação:

0 + 2 exp(−1) 6 f ′(x) = 3x2 + 2 exp(−x) 6 3 + 2

0.7358 6 f ′(x) 6 5

Então, m = 0.7358 e o critério de paragem vem |f(xn)| 6 0.7358× 10−3.

Aproximação inicial: (a0 = 0, b0 = 1).Processo iterativo:Os valores obtidos no processo iterativo são apresentados na tabela a seguir, sendo

o critério de paragem |f(xn)| 6 0.7358 × 10−3 testado no fim de cada iteração (vercoluna da direita na tabela que se segue).

Note-se que este critério de paragem foi deduzido na hipótese de a aproximaçãoestar numa vizinhança suficientemente pequena do zero.

Se o cálculo da derivada for simples de obter, pode ajustar-se em cada iteração ovalor de m através da seguinte aproximação m ≈ f ′(x).


0 0 −2 1 +0.2642 0.88329 −0.13771 0.88329 −0.1377 1 +0.2642 0.92327 −(0.7404)10−2

2 0.92327 −(0.7404)10−2 1 +0.2642 0.92536 −(0.3843)10−3

A aproximação do zero obtida pelo método da Falsa Posição é z = 0.925365.O extremo bk imobilizou-se no ponto x = 1. A convergência nestas situações pode

ser acelerada utilizando a variante de Illinois ([Pina(1995)]).

iii) Método da Secante (Ordem de convergência(1 +

√5)/2 ≈ 1.618 para zeros

simples):1. Aproximação inicial ao zero.Sejam (x−1, f(x−1)), (x0, f(x0)) duas estimativas iniciais.2. Processo iterativo:Aplicar de forma sucessiva a seguinte expressão com k = 0, 1, 2, ...

xk+1 = xk − f(xk)f [xk−1, xk]

onde f [xk−1, xk] =f(xk)− f(xk−1)

xk − xk−1


3. Critério de paragem:

i) |f(xn)| 6 mε,

ou

ii) |xk+1 − xk| 6 mε.

Utiliza-se ii) caso z seja um zero simples. Caso não se saiba ou não o seja, utiliza-seo critério universal i) onde m é o minorante da primeira derivada, f ′(x), no intervalo.

Deste modo, temos para este problema com o método da secante a mesma expres-são |f(xn)| 6 0.7358× 10−3 utilizada no método da Falsa Posição.

Aproximação inicial: (a0 = 0, b0 = 1).Processo iterativo:Os valores obtidos no processo iterativo são apresentados na tabela a seguir, sendo

o critério de paragem |f(xn)| 6 0.7358 × 10−3 testado no fim de cada iteração (vercoluna da direita na tabela que se segue).

k xk f(xk) xk+1 f(xk+1)

0 1 +0.26424 0.88329 −0.13771 0.88329 −0.13767 0.92327 −(0.7404)10−2

2 0.92327 −(0.7404)10−2 0.92554 −(0.2236)10−3

A aproximação do zero obtida pelo método da Secante é z = 0.92554. Note-se quepelo critério ii) seria necessário continuar o processo iterativo até k = 3. ¥

Em ambiente de MATLAB encontram-se várias aplicações (funções do MATLAB)para a determinação de zeros de funções. No caso de funções de uma variável o al-goritmo utilizado combina os métodos da bissecção, secante e interpolação inversaquadrática. Uma implementação em FORTRAN deste algoritmo encontra-se emForsythe, G. E., M. A. Malcolm, and C. B. Moler, Computer Methods for Mathema-tical Computations, Prentice-Hall, 1976.

A determinação de zeros de funções não-lineares com mais de uma variável estáfora dos objectivos deste livro, apenas se referindo que em MATLAB se utiliza afunção fsolve. Os algoritmos utilizados são os do método de Gauss-Newton, deLevenberg-Marquardt e em problemas de grande dimensão recorre-se a métodos dosmínimos quadrados.

No caso particular de polinómios utiliza-se a função root que se baseia num algo-ritmo de cálculo de valores e vectores próprios de uma matriz associada ao problema.

Para uma leitura mais detalhada sobre este assunto recomenda-se a consulta darespectiva parte do manual do MATLAB e as referências indicadas. ¡

10.2 EQUAÇÕES NÃO-LINEARES:

Método da Bissecção e zeros múltiplos

Indique como se comporta o método da bissecção no caso de zeros múltiplos? Consi-dere para a resposta, os casos de zeros de multiplicidade par e multiplicidade ímpar.

80 SEMANA 10

CONCEITOS TEÓRICOSA Figura 10.2.1 exemplifica alguns dos diferentes tipos de zeros e a tabela define

as características de zeros simples, duplos e triplos (ver definição 5.1.2 e teorema 5.1.1em Pina[1995]).

−10 −8 −6 −4 −2 0 2 4 6 8 10−10

−8

−6

−4

−2

0

2

4

6

8

10

(a) f(x) = x: Zero simples−10 −8 −6 −4 −2 0 2 4 6 8 10

−100

−80

−60

−40

−20

0

20

40

60

80

100

(b) f(x) = x2: Zero duplo−10 −8 −6 −4 −2 0 2 4 6 8 10

−1000

−800

−600

−400

−200

0

200

400

600

800

1000

(c) f(x) = x3: Zero triploFigura 10.2.1: Exemplos de funções com zeros de diferentes multiplicidades

Tabela 10.2.1: Características dos zeros simples, duplos e triplos.

a) b) c)

Zero simples Zero duplo Zero triplo

f(z) = 0 f(z) = f ′(z) = 0 f(z) = f ′(z) = f ′′(z) = 0

f ′(z) 6= 0 f ′′(z) 6= 0 f ′′′(z) 6= 0

Em termos geométricos, dizemos que ao zero simples corresponde um declive nãonulo, ao zero duplo corresponde um declive nulo, mas curvatura não nula, e ao zerotriplo um declive e uma curvatura nulos. ¤

RESOLUÇÃONo caso de multiplicidade par, o método da bissecção não pode iterar por não ser

possível encontrar um intervalo

I = [a, b] : f(a)× f(b) < 0

.No caso de multiplicidade ímpar o método da bissecção funciona num intervalo

com mudança de sinal nos valores da função para os extremos do intervalo. ¥


Método da Falsa Posição

O cálculo da carga crítica de instabilidade de Euler de uma estrutura, conduziu àseguinte equação: f(x) = x(x2 − 120) sin(x) − 24(x2 + 12) cos(x) + 288 = 0. Daanálise de casos-limite sabe-se que a solução da equação está situada no intervalo[π, 2π]. Usando este intervalo inicial, efectue 4 iterações pelo método da falsa posição


para obter uma solução aproximada x4. Verifique, justificando, se o erro absoluto dex4 na aproximação ao zero nesse intervalo é inferior a 10−4.

RESOLUÇÃOPelo teorema do valor intermédio, se f(x) for uma função contínua, existe um

ponto z ∈ [π, 2π] : f(z) = 0.A função f(x) é contínua verificando-se que:

f(x) = x(x2 − 120) sin(x)− 24(x2 + 12) cos(x) + 288 = 0

f(π) = 812.87

f(2π) ≈ −947.48

f(π)× f(2π) < 0

Método da Falsa Posição (Ordem de convergência 1 para zeros simples):1. Aproximação inicial ao zero.Sejam (ak, f(ak)), (bk, f(bk)) duas estimativas iniciais.2. Processo iterativo:

xk+1 =akf(bk)− bkf(ak)

f(bk)− f(ak)

f(ak)× f(xk+1) < 0 ⇒ ak+1 = ak, bk+1 = xk+1

f(ak)× f(xk+1) > 0 ⇒ ak+1 = xk+1, bk+1 = bk

A aproximação inicial é a0 = π, b0 = 2π.Os resultados do processo iterativo até obter x4 são apresentados na seguinte

tabela.


0 (.31415)10+1 +(.81287)10+3 (.62831)10+1 −(.94748)10+3 (.45922)10+1 +(.83411)10+3

1 (.45922)10+1 +(.83411)10+3 (.62831)10+1 −(.94748)10+3 (.53839)10+1 +(.59571)10+2

2 (.53839)10+1 +(.59571)10+2 (.62831)10+1 −(.94748)10+3 (.54371)10+1 −(.51381)10+1

3 (.53839)10+1 +(.59571)10+2 (.54371)10+1 −(.51381)10+1 (.54329)10+1 +(.23102)10−1

A aproximação obtida pelo método da Falsa Posição é x4 = 5.4329.A verificação do erro absoluto de x4 faz-se da seguinte forma:E = |z − x4| < 10−4 ↔ f(x4) < mε

sendo o valor de m obtido no ponto x4 por:f ′(x) = (27x2 + 168) sin(x) + (x3 − 168x) cos(x),f ′(x4) = f ′(5.432901) = 1221.5.Com este valor de m, verifica-se que:f(x4) = 0.023102 < 1221.5× 10−4 = 0.12215,confirmando-se de facto que o erro absoluto é Ex4 < 10−4. ¥

11

TÓPICOS: Equações Não-Lineares (cont.): Natureza e localização de zerosde polinómios (Regra de Descartes e de Budan); Método de Newton-Raphson; Métododo ponto fixo e aceleração de Aitken. Localização de zeros de polinómios.



Natureza e localização de zeros de polinómios

(metodologia)

Para o polinómio p(x) = x3 + 2x2 + 10x− 20:

a) Determine a natureza dos seus zeros,

b) Obtenha a localização do zero positivo, e

c) Determine o zero positivo pelo método da secante com 3 decimais exactos.

RESOLUÇÃO

a)

Natureza dos zeros

Aplicando a regra dos sinais de Descartes I (p. 192, [Pina(1995)]) ao polinómio

p(x) = x3 + 2x2 + 10x− 20, observa-se que o número V de mudanças de sinal doscoeficientes do polinómio permite concluir pela existência de um zero real positivo,i.e.,

N+ 6 V = 1

V −N+ é par

⇒ N+ = 1 (1 zero real positivo)

Aplicando agora a regra dos sinais de Descartes II (p. 192-3, [Pina(1995)]) constrói-se o polinómio p(−x):

q(x) = p(−x) ⇔ q(x) = −x3 + 2x2 − 10x − 20 onde se observa que o númeroV de mudanças de sinal dos coeficientes do polinómio p(−x) permite concluir pelaexistência de nenhum zero real negativo ou dois, i.e.,

84 SEMANA 11

V = 2 ⇒ N− 6 2

V −N− é par

⇒ N− = 0 ∨ N− = 2 (0 ou 2 zeros reais negativos)

Por fim, tratando-se de um polinómio de grau 3 pode concluir-se que o polinómiop(x) tem duas possibilidades:

i) 1 zero real positivo e 2 zeros reais negativos, ou

ii) 1 zero real positivo e 2 zeros complexos.

b)

Localização dos zeros do polinómio

Pelo Teorema 5.9.1 (p. 193, [Pina(1995)]) os zeros do polinómio estão no interiorde um círculo centrado na origem de raio:

Ω = 1 + max06k6n−1

∣∣∣∣ak

an

∣∣∣∣ .

Com n = 3 e com os os coeficientes ak do polinómio obtém-se o valor:

Ω = 1 + max06k62

∣∣∣∣ak

a3

∣∣∣∣ = 1 + 20 = 21.

Todos os zeros do polinómio p(x) estão situados no círculo do plano complexocentrado na origem e de raio 21.

Verificação: Pode-se testar se existe mudança de sinal no valor do polinómio entredois pontos do intervalo [0, 21], i.e.

p(x) = x3 + 2x2 + 10x− 20 ⇒

p(0) = −20p(21) = 10333

observando-se que p(0)× p(21) < 0.

Pelo teorema do valor intermédio, se f(x) for uma função contínua, existe umponto z ∈ [0, 21] : f(z) = 0.

Podemos ainda proceder ao refinamento do intervalo onde se encontra o zero realpositivo utilizando a Regra de Budan (p. 195, [Pina(1995)]) num intervalo. para issoprecisamos das derivadas até à ordem n do polinómio .

p(x) = x3 + 2x2 + 10x− 20

p′(x) = 3x2 + 4x + 10

p′′(x) = 6x + 4

p′′′(x) = 6

Para um intervalo [a, b] = [0, 2] tem-se:


a = 0 : p(0) = −20; p′(0) = 10; p′′(0) = 4; p′′′(0) = 6

b = 2 : p(2) = 16; p′(2) = 30; p′′(2) = 16; p′′′(2) = 6

onde pela regra de Budan se concluí que

N 6 Va − Vb = 1

(Va − Vb)−N é par

⇒ N = 1 (1 zero real positivo no intervalo [0, 2]),

i.e., o zero real está neste intervalo.

Por fim sugere-se que aplique a regra de Budan ao intervalo [2, 21].

c)

Método da Secante (Ordem de convergência(1 +

√5)/2 ≈ 1.618 para zeros

simples):

Aproximação inicial: Sejam os pontos (x−1, f(x−1)), (x0, f(x0)) duas estimativasiniciais.

Processo iterativo:Itera-se sucessivamente em k=0,1,2,...

xk+1 = xk − f(xk)f [xk−1, xk]

onde f [xk−1, xk] =f(xk)− f(xk−1)

xk − xk−1

Critério de paragem:

|f(xn)|M

6 |en| 6 |f(xn)|m

M |z − xn| 6 |f(xn)| 6 m |z − xn|

Logo

|f(xn)| 6 mε

onde m é o minorante da primeira derivada, f ′(x), no intervalo.

Tratando-se de um zero simples pode utilizar-se também o seguinte critério deparagem:

|xk+1 − xk| ≤ ε

Neste problema como pretendemos 3 decimais exactas no intervalo [0, 2], entãoε = 10−3. Para utilizar o critério universal calcula-se da seguinte forma o minorante,m:

f(x) = p(x) = x3 + 2x2 + 10x− 20

f ′(x) = p′(x) = 3x2 + 4x + 10

f ′′(x) = p′′(x) = 6x + 4 > 0 no intervalo [0, 2], logo aí f ′(x) é monótona crescente.

86 SEMANA 11

Conclui-se de

10 6 3x2 + 4x + 10 6 30,

que o minorante m ocorre em x = 0, com valor m = 10 e por isso o critério de paragemserá |f(xn)| 6 10× 10−3 = 10−2.

Aproximação inicial: x−1 = 0, x0 = 2

Processo iterativo: Os resultados encontram-se na seguinte tabela.

k xk f(xk) xk+1 f(xk+1)

0 2 16 1.11111 −5.04801 1.11111 −5.0480 1.32429 −0.92702 1.32429 −0.9270 1.37225 +0.07273 1.37225 +0.0727 1.36876 −0.0009

A aproximação do zero obtida pelo método da Secante é z = 1.36876, pois

|f(x4)| 6 mε.

¥


Método de Newton-Raphson

a) Verifique que a função f(x) = 16 exp(x)−48+27 exp(−x) tem um zero no intervalo[0.5, 1] e outro no intervalo [−0.5, 0]. Verifique também que não existem mais zeros(justifique).

b) Pretende-se obter uma aproximação do zero positivo da equação f(x) = 0. Par-tindo de x0 = 1.0, efectue 3 iterações de Newton-Raphson. Verifique se o erro daaproximação de x3 ao zero é inferior a 10−5.

RESOLUÇÃO

a) A função

f(x) = 16 exp(x)− 48 + 27 exp(−x)

tem os seguintes limites:

limx→±∞

f(x) = +∞,

e a sua derivada

f ′(x) = 16 exp(x)− 27 exp(−x)

anula-se no ponto

f ′(x) = 0 ⇔ 16 exp(x)− 27 exp(−x) = 0 ⇔ x = 0.26162.


Se x ∈]−∞, 0.26162[, f ′(x) < 0 ⇒ f(x) é monótona decrescente.

Se x ∈]0.26162,+∞[, f ′(x) > 0 ⇒ f(x) é monótona crescente.

Logo, como f(0.26162) = −6.43 < 0, então existe um único zero no intervalo]−∞, 0.26162[ e mais outro único zero no intervalo ]0.261624, +∞[.

b)

Método de Newton-Raphson (Ordem de convergência 2 para zeros simples)


Seja x0 uma estimativa inicial do zero.

2. Processo iterativo:

Itera-se sucessivamente em k=0,1,2,... utilizando a seguinte expressão:

xk+1 = xk − f (xk)f ′ (xk)

Aproximação inicial: x0 = 1

Processo iterativo: São pedidas 3 iterações. Os resultados são apresentados naseguinte tabela.

k xk f(xk) f ′(xk)

0 1 (.5425)101 (.33559)102

1 0.83833 (.6760)100 (.25324)102

2 0.81164 (.1726)10−1 (.24034)102

3 0.81093 (.1881)10−4

A aproximação ao zero é z = 0.81093.

Para a verificação do erro absoluto em x3 faz-se:

E = |z − x3| < 10−5 ⇒ f(x3) < mε,

f ′(x) = 16 exp(x)− 27 exp(−x),

f ′(x3) = f ′(0.81093) = (.23998)102,

f(x3) = (.1881)10−4 < (.23998)102 × 10−5 = (.23998)10−3.

Confirma-se que Ex3 < 10−5.

Poderia ter utilizado o critério aplicável a converg encias supralineares já que setrata de um zero simples. ¥

88 SEMANA 11

As Figuras 11.2.1 e 11.2.2 mostram a função f(x) e a sua derivada no intervalo[−1, 1].

−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1−10

−5

0

5

10

15

20

25

30

35

Figura 11.2.1: Função f(x) = 16 exp(x)− 48 + 27 exp(−x) no intervalo [−1, 1]

−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1−80

−60

−40

−20

0

20

40

Figura 11.2.2: Função f ′(x) = 16 exp(x)− 27 exp(−x) no intervalo [−1, 1]

¡


Método do Ponto Fixo. Localização de zeros de

polinómios e aceleração de Aitken

Determine com 5 dígitos correctos o zero positivo da equação x3 − x2 − x − 1 = 0utilizando o método do Ponto Fixo.


CONCEITOS TEÓRICOSTeorema 5.8.1 para a convergência do método do Ponto Fixo (p. 186, [Pina(1995)]):

Se existir um intervalo I ⊂ [a, b] tal que g(I) ⊂ I e relativamente ao qual a função g écontractiva, |g′(x)| < 1, então esta função possui um único ponto fixo neste intervalo,e a sucessão xk gerada por xk+1 = g(xk), com k = 0, 1, . . . converge para este pontofixo qualquer que seja a estimativa inicial x0 ∈ I.

Uma função g(x) contínua num intervalo I diz-se contractiva nesse intervalo se|g′(x)| < 1 para todo x ∈ I.

Observando a Figura 11.3.1 constatamos que o método do ponto fixo tem comobase geométrica a determinação do ponto de intersecção de g(x) com a recta y = x,correspondendo este ponto ao zero da função f(x). Ou seja, transforma-se o problemade localização de zeros de f(x) no problema matematicamente equivalente de deter-minação da intersecção da g(x) com a recta y = x. A vantagem é, como veremos, emtermos de algoritmo o mais simples que se pode obter.

Dada uma aproximação inicial x0 o processo iterativo consiste simplesmente emcalcular sucessivamente para k = 0, 1, ...:

xk+1 = g (xk)

A prova de convergência pode tornar-se num problema de alguma dificuldade.Em termos práticos, podemos limitarmo-nos a verificar se existe convergência dosresultados numéricos para o ponto fixo da função no intervalo pretendido.

Na Figura estão exemplificados os casos: a) processo iterativo convergente e b)processo iterativo divergente. Quer os casos convergentes, quer os divergentes, podemocorrer em "escada"ou por "envolvente".

(a) Convergência (b) Divergência

Figura 11.3.1: Convergência e divergência do método do ponto fixo

Aceleração de Aitken: Como escreve [Pina(1995)] na p. 188: Se g′(z) 6= 0,a convergência do método iterativo de ponto fixo é linear, o que, frequentementesignifica que é lenta. No entanto, é possível acelerar a convergência por um processodevido a Aitken.

A fórmula para proceder à aceleração de Aitken é:

x′k = xk − (∆xk)2

∆2xk

90 SEMANA 11

onde se tem o operador de diferença progressiva:

∆xk = xk+1 − xk e ∆2xk = xk+2 − 2xk+1 + xk,

ou seja,

x′k,m+1 = xk,m − (xk+1,m − xk,m)2

xk+2,m − 2xk+1,m + xk,mcom k, m = 0, 1, ...

O indíce m é para o cálculo com a aceleração de Aitken.

RESOLUÇÃOMétodo do ponto fixo (Ordem de convergência 1):Como é pedido para aplicar o método do ponto fixo, considere-se a equação f(x) =

0 escrita na forma x = g(x). De imediato verificamos que podemos escolher váriasfunções g(x), mas como se verá nem todas são escolhas válidas para utilizar com estemétodo. Para cada função escolhida verificam-se as condições de convergência.

Escolha-se a seguinte função.Função 1: g(x) = x3 − x2 − 1 = x(3x− x)

Para se garantir que o processo é convergente teremos desde já que verificar se|g′(x)| < 1 num intervalo I que contenha a raiz e depois se g(I) ⊂ I .

Convergência:O processo não é convergente em todos os pontos, poisg′(x) = 3x2 − 2x = 3x(x− 2)

dependendo do intervalo escolhido poderá em módulo ser maior do que 1.Neste problema não nos é indicado um intervalo que contenha o zero, pelo que

temos de determinar uma localização dos zeros desta função polinomial.Localização dos zerosPelo Teorema 5.9.1 (p. 193, [Pina(1995)]):

Ω = 1 + max06k6n−1

∣∣∣∣ak

an

∣∣∣∣

Com n = 3, fica

Ω = 1 + max06k62

∣∣∣∣ak

a3

∣∣∣∣ = 1 + 1 = 2

Todos os zeros estão situados no círculo do plano complexo de raio 2.Verificação:

p(x) = x3 − x2 − x− 1 ⇒

p(0) = −1p(2) = 1

p(0)× p(2) < 0

Pelo teorema do valor intermédio (p. 315 do livro [Ferreira(1985)]), se f(x) foruma função contínua, existe um ponto z ∈ [0, 2] : f(z) = 0.


Um refinamento do intervalo onde se encontra o zero real positivo pode ser deter-minado pela Regra de Budan (p. 195, [Pina(1995)]):

p(x) = x3 − x2 − x− 1,

p′(x) = 3x2 − 2x− 1,

p′′(x) = 6x− 2,

p′′′(x) = 6,

onde para verificar se o zero está no intervalo [0, 1] basta fazer:

a = 0 : p(0) = −1; p′(0) = −1; p′′(0) = −2; p′′′(0) = 6

b = 1 : p(1) = −2; p′(1) = 0; p′′(1) = 4; p′′′(1) = 6

N 6 Va − Vb = 0

(Va − Vb)−N é par

⇒ N = 0 (0 zeros reais positivo no intervalo [0, 1])

O zero real positivo está localizado no intervalo [1, 2], pois não existe nenhum em[0, 1], como verificámos.

Ora, para x > 1 facilmente se conclui que g′(x) = 3x(x − 2) em módulo é maiordo que 1. Temos por isso que escolher outra função que esta não possui as condiçõesde convergência.

Função 2:

Como f(x) = x3 − x2 − x− 1, pode obter-se para g(x) a seguinte função:

g(x) = (x2 + x + 1)1/3

Como anteriormente referido, para se garantir que o processo é convergente temque se assegurar que |g′(x)| < 1 num intervalo que contenha a raiz.

Ora

g′(x) =13

2x + 1(x2 + x + 1)2/3

,

não sendo óbvio que no intervalo [1, 2] se tenha |g′(x)| < 1. Para isso vai-se estudara segunda derivada:

g′′(x) =13

2(x2 + x + 1)2/3 − (2x + 1)22/3(x2 + x + 1)−1/3

(x2 + x + 1)4/3,

onde, multiplicando a segunda parcela do numerador por

(x2 + x + 1)(x2 + x + 1)

,

permite obter a expressão:

92 SEMANA 11

g′′(x) =23

(x2 + x + 1)2/3[1− 13

(2x+1)2

(x2+x+1) ]

(x2 + x + 1)2/3,

g′′(x) =−29

(x2 + x− 2)(x2 + x + 1)5/3

.

Pode agora concluir-se que para x ∈ [1, 2] se terá g′(x) monotona decrescente. Éagora suficiente conhecer os valores da derivada nos extremos deste intervalo.

g′(x) =13

2x + 1(x2 + x + 1)2/3

⇒

g′(1) ≈ 0.48075 < 1

g′(2) ≈ 0.45546 < 1

Falta verificar que g(I) ⊂ I. Como no intervalo x ∈ [1, 2] se verifica

g′(x) =13

2x + 1(x2 + x + 1)2/3

,

então a função g(x) é monotona. Basta agora verificar o que se passa nos extremosdo intervalo.

g(x) = (x2 + x + 1)1/3 ⇒

g(1) ≈ 1.4422 ∈ [1, 2]g(2) ≈ 1.9129 ∈ [1, 2]

Como [g(1), g(2)] ⊃⊂ [1, 2] estão assim garantidas as condições de convergênciapara o ponto fixo no caso da segunda função.

1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2−2

−1.5

−1

−0.5

0

0.5

1

Figura 11.3.2: Polinómio x3 − x2 − x− 1 no intervalo [1, 2]


1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 21.4

1.5

1.6

1.7

1.8

1.9

2

(a) Função g(x)1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2

0.32

0.34

0.36

0.38

0.4

0.42

0.44

0.46

0.48

0.5

(b) Função g′(x)

Figura 11.3.3: Funções g(x) e g′(x) no intervalo [1, 2]

A aproximação inicial pode agora ser escolhida como x0 = 1.5.O processo iterativo consiste simplesmente em calcular sucessivamente para k=0,1,...:

xk+1 = g (xk)

O critério de paragem de acordo com o enunciado do Problema 5.13.32 em [Pina(1995)](sugere-se a resolução desse problema), para o método do ponto fixo prevê a seguintecondição:

|ek| 6 M

1−M|xk − xk−1| onde |g′(x)| 6 M < 1 em I = [a, b],

onde, se M 6 1/2 então

|ek| 6 |xk − xk−1| ⇒ |xk − xk−1| < ε

Como são pedidos 5 dígitos correctos e tendo em conta que o zero está localizadoentre 1 e 10 (em ordem de grandeza) então

ε = 10−5 × 101 = 10−4 ou seja quatro decimais correctos.

k xk |xk − xk−1|0 1.51 1.6809 (.18)100

2 1.7658 (.85)10−1

3 1.8053 (.39)10−1

4 1.8236 (.18)10−1

5 1.8320 (.84)10−2

6 1.8359 (.39)10−2

7 1.8377 (.18)10−2

8 1.8385 (.83)10−3

9 1.8389 (.38)10−3

10 1.8391 (.18)10−3

11 1.8392 (.80)10−4

Verifica-se que |x11 − x10| = (.80)10−4 < 10−4, pelo que a aproximação do zeroobtida pelo método do ponto fixo é z = (.18392)101.

94 SEMANA 11

Aceleração de Aitken: Depois de calculados x0, x1 e x2 podemos usar a acele-ração de Aitken, ou seja

k x′k |x′k − x′k−1|0 1.84091 1.8396 (.12)10−2

2 1.8393 (.28)10−3

3 1.8392 (.90)10−4

4 1.8393 (.40)10−4

5 1.8392 (.50)10−4

Verifica-se que |x′5 − x′4| = (.50)10−4 < 10−4, pelo que a aproximação do zeroobtida pelo método do ponto fixo é z = (.18392)101.

Bastava pararmos em k = 3, dado que |x′3 − x′2| = (.90)10−4. ¥

12

TÓPICOS: Sistemas de Equações Lineares: Método de Gauss; Método deGauss com escolha de pivot total; Método de Gauss com escolha de pivot parcial.LEITURAS RECOMENDADAS: Capítulo 6 (pp. 211–240) do livro [Pina(1995)]

12.1 SISTEMAS DE EQUAÇÕES LINEARES:

Método de Gauss

Resolva pelo método de Gauss o seguinte sistema de equações lineares:

x1 + x2 + x3 = 4

x1 − x2 + 2x3 = 4

2x1 + x2 + x3 = 5

ALGORITMOAlgoritmo para o método de condensação de Gauss:Transformar por n-1 etapas sucessivas a matriz A numa matriz triangular supe-

rior.Ciclo de k = 1, 2, ..., n-1 (coluna a factorizar)Ciclo de i = k+1, 2, ..., n (linhas abaixo do pivot akk)

mik = a(k)ik /a

(k)kk (o pivot akk não pode ser nulo)

Ciclo de j = k+1, 2, ..., n (colunas à direita do pivot akk)a(k+1)ij = a

(k)ij − mik × a

(k)kj

b(k+1)i = b

(k)i − mik × b

(k)k

Continuar ciclo em j

Continuar ciclo em i

Continuar ciclo em k

Algoritmo para as substituições ascendentes:Ciclo de i = n, n-1,...,1 (linhas)

sum=0

Ciclo de k = i+1, ..., n

sum = sum + aik × xk


x(n−1)i =

(b(n−1)i − sum

)/aii

Continuar ciclo em i ¤

96 SEMANA 12

RESOLUÇÃO

Sistema de equações Ax = b escrito na forma matricial:

1 1 11 −1 22 1 1

x1

x2

x3

=

445

Condensação:

Procedendo sucessivamente, obtemos

k = 1:

1 1 1 41 −1 2 42 1 1 5

m21 =a(1)21

a(1)11

=11

= 1

a(2)22 = a

(1)22 −m21a

(1)12 = −1− 1× 1 = −2

a(2)23 = a

(1)23 −m21a

(1)13 = 2− 1× 1 = 1

b(2)2 = b

(1)2 −m21b

(1)1 = 4− 1× 4 = 0

m31 =a(1)31

a(1)11

=21

= 2

a(2)32 = a

(1)32 −m31a

(1)12 = 1− 2× 1 = −1

a(2)33 = a

(1)33 −m31a

(1)13 = 1− 2× 1 = −1

b(2)3 = b

(1)3 −m31b

(1)1 = 5− 2× 4 = −3

k = 2:

1 1 1 40 −2 1 00 −1 1 −3


m32 =a(2)32

a(2)22

=−1−2

=12

a(3)33 = a

(2)33 −m32a

(2)23 = −1− 1

2× 1 = −3

2

b(3)3 = b

(2)3 −m32b

(2)2 = −3− 1

2× 0 = −3

1 1 1 40 −2 1 00 0 −3/2 −3

O sistema fica então,

1 1 10 −2 10 0 −3/2

x1

x2

x3

=

40−3

Por substituição ascendente obtém-se:

−32x3 = −3 ⇔ x3 = 2,

−2x2 + x3 = 0 ⇔ −2x2 + 2 = 0 ⇔ x2 = 1,

x1 + x2 + x3 = 4 ⇔ x1 + 1 + 2 = 4 = 0 ⇔ x1 = 1.

A solução do sistema de equações é:

x1

x2

x3

=

112

¥


Método de Gauss com escolha de pivot total

Considere os sistemas de equações cujas matrizes A e segundos membros b são dadospor:

aij = (i− j)2/(i + j), i, j = 1, . . . , n; bk = 1/k, k = 1, . . . , n

Resolva o sistema em aritmética exacta para n = 3 pelo método de Gauss comescolha de pivot total.

98 SEMANA 12

CONCEITOS TEÓRICOS E ALGORITMOS

Método de Gauss com escolha de pivot total: Consiste em transformar por etapassucessivas a matriz A numa matriz triangular superior. De acordo com a técnicade pivot total, são candidatos a pivot todos os elementos a

(k)ij , i, j = k, . . . , n, ou

seja, todos os elementos abaixo e à direita de a(k)kk incluindo o póprio, i.e., todos os

elementos da parte activa de A(k), determinando-se dois índices pk e qk tais que

∣∣∣a(k)pkqk

∣∣∣ = maxk6i,j6n

|aij |

Se pk 6= k trocam-se as linhas k e pk e se qk 6= k efectua-se também uma trocadas colunas k e qk.

Trocadas as linhas e colunas no início da etapa, quando da escolha de pivot, afactorização prossegue como no método sem escolha de pivot.

Apenas convém reter os índices de troca de colunas já que correspondem a trocade variáveis.

Algoritmo para o método de condensação de Gauss com pivot total:

Ciclo de k = 1, 2, ..., n-1 (coluna a condensar)

Escolher pivot (total) tal que∣∣∣a(k)

kk

∣∣∣ = maxk6i,j6n

∣∣aij∣∣

Trocar as linhas e colunas necessárias

Registar as trocas de coluna efectuadas

Ciclo de i = k+1, 2, ..., n (linhas abaixo do pivot akk)

mik = a(k)ik /a


Ciclo de j = k+1, 2, ..., n (colunas à direita do pivot akk)

a(k+1)ij = a

(k)ij − mika

(k)kj


b(k+1)i = b

(k)i − mikb

(k)k



Algoritmo para as substituições ascendentes:

Ciclo de i = n, n-1,...,1 (linhas)

sum=0




x(n−1)i =

(b(n−1)i − sum

)/aii


Caso se tenha procedido a alguma troca de colunas repôr os indíces de acordo comas trocas realizadas. ¤


RESOLUÇÃO

Com n = 3 temos o seguinte sistema de equações Ax = b escrito na formamatricial:

0 1/3 11/3 0 1/51 1/5 0

x1

x2

x3

=

11/21/3

Este sistema só pode ser resolvido com troca de linhas ou colunas, já que os valoreszero na posição de pivot não são admissíveis.

Permutação e condensação:


k = 1:

0 1/3 1 11/3 0 1/5 1/21 1/5 0 1/3

x1 x2 x3

Trocar a 1.a linha com a 3.a linha (não afecta a ordem das variáveis):

1 1/5 0 1/31/3 0 1/5 1/20 1/3 1 1

x1 x2 x3

m21 =a(1)21

a(1)11

=1/31

=13

a(2)22 = a

(1)22 −m21a

(1)12 = 0− 1

3× 1

5= − 1

15

a(2)23 = a

(1)23 −m21a

(1)13 =

15− 1

3× 0 =

15

b(2)2 = b

(1)2 −m21b

(1)1 =

12− 1

3× 1

3=

718

k = 2:

1 1/5 0 1/30 −1/15 1/5 7/180 1/3 1 1

x1 x2 x3

100 SEMANA 12

A escolha de pivot na submatriz activa requer trocar a 2.a linha com a 3.a linhaseguida de troca da 2.a coluna com a 3.a coluna:

1 0 1/5 1/30 1 1/3 10 1/5 −1/15 7/18

x1 x3 x2

A condensação prossegue da mesma forma:

m32 =a(2)32

a(2)22

=1/51

=15

a(3)33 = a

(2)33 −m32a

(2)23 = − 1

15− 1

5× 1

3= − 2

15

b(3)3 = b

(2)3 −m32b

(2)2 =

718− 1

5× 1 =

1790

obtendo-se:

1 0 1/5 1/30 1 1/3 10 0 −2/15 17/90

x1 x3 x2

O sistema fica então com a ordem das variáveis trocada em resultado da troca decolunas anteriormente efectuada:

1 0 1/50 1 1/30 0 −2/15

x1

x3

x2

=

1/31

17/90

Por substituição ascendente obtém-se:

− 215

x2 =1790⇔ x2 = −17

12

x3 +13x2 = 1 ⇔ x3 +

13×

(−17

12

)x2 = 0 ⇔ x3 =

5336

x1 +15x2 =

13⇔ x1 +

15×

(−17

12

)=

13⇔ x1 =

3760

A solução do sistema de equações é dada por:

x1

x2

x3

=

+37/60−17/12+53/36

¥



Método de Gauss com escolha de pivot parcial

Considere a matriz An×n com n = 4 cujas entradas aij são definidas para i, j =1, 2, ..., n de acordo com a seguinte regra e o vector b indicado.

aij =

2/i; i = j

1/|i− j|; i 6= j

bi = (0 1 0 0)T

Resolva o sistema de equações lineares Ax = b pelo método de Gauss com escolhade pivot parcial. Faça as operações com a precisão da sua calculadora mas apresenteos resultados (intermédios e finais) em FP (10, 4, 2, A).

CONCEITOS TEÓRICOSMétodo de Gauss com pivot parcial: Transformar por etapas sucessivas a matriz

A numa matriz triangular superior. De acordo com a técnica de pivot parcial, sãocandidatos a pivot os elementos a

(k)ik , i = k, . . . , n da matriz A(k), escolhendo-se

aquele que tiver maior valor absoluto na parte activa da respectiva coluna. Maisprecisamente, seja pk um índice tal que

∣∣∣a(k)pkk

∣∣∣ = maxk6i6n

∣∣∣a(k)ik

∣∣∣

Se pk 6= k procede-se à permuta das linhas k e pk.Trocadas as linhas, a aplicação do algoritmo prossegue normalmente, não havendo

necessidade de registar as trocas para o cálculo das incógnitas já que trocas de linhanão afectam a ordem das incógnitas.

Algoritmo para o método de condensação de Gauss com pivot parcial:Ciclo de k = 1, 2, ..., n-1 (coluna a condensar)

Escolher pivot (parcial) tal que∣∣∣a(k)

kk

∣∣∣ = maxk6i6n

∣∣aij∣∣

Trocar as linhas e colunas necessárias

Ciclo de i = k+1, 2, ..., n (linhas abaixo do pivot akk)mik = a

(k)ik /a


Ciclo de j = k+1, 2, ..., n (colunas à direita do pivot akk)a(k+1)ij = a

(k)ij − mika

(k)kj


b(k+1)i = b

(k)i − mikb

(k)k



Algoritmo para as substituições ascendentes:Ciclo de i = n, n-1,...,1 (linhas)

sum=0


102 SEMANA 12



x(n−1)i =

(b(n−1)i − sum

)/aii


RESOLUÇÃO

O sistema de equações Ax = b a resolver pode ser escrito na seguinte forma:

2 1 0.5 0.33331 1 1 0.5

0.5 1 0.6667 10.3333 0.5 1 0.5

x1

x2

x3

x4

=

0100

Permutação e condensação:

Procedendo sucessivamente à condensação de acordo com o algoritmo, fazendo oscálculos na precisão da calculadora e escrevendo os valores em FP tem-se:

k = 1:

2 1 0.5 0.3333 01 1 1 0.5 1

0.5 1 0.6667 1 00.3333 0.5 1 0.5 0

(.2000)10+01 (.1000)10+01 (.5000)1000 (.3333)1000 (.0000)1000

(.1000)10+01 (.1000)10+01 (.1000)10+01 (.5000)1000 (.1000)10+01

(.5000)1000 (.1000)10+01 (.6667)1000 (.1000)10+01 (.0000)1000

(.3333)1000 (.5000)1000 (.1000)10+01 (.5000)1000 (.0000)1000

Não é necessário trocar linhas.

m21 =a(1)21

a(1)11

=12

= 0.5

a(2)22 = a

(1)22 −m21a

(1)12 = 1− 0.5× 1 = 0.5 = (.5000)1000

a(2)23 = a

(1)23 −m21a

(1)13 = 1− 0.5× 0.5 = 0.75 = (.7500)1000

a(2)24 = a

(1)24 −m21a

(1)14 = 0.5− 0.5× 0.3333 = 0.33335 = (.3334)1000

b(2)2 = b

(1)2 −m21b

(1)1 = 1− 0.5× 0 = 1 = (.1000)10+01


m31 =a(1)31

a(1)11

=0.52

= 0.25

a(2)32 = a

(1)32 −m31a

(1)12 = 1− 0.25× 1 = 0.75 = (.7500)1000

a(2)33 = a

(1)33 −m31a

(1)13 = 0.6667− 0.25× 0.5 = 0.5417 = (.5417)1000

a(2)34 = a

(1)34 −m31a

(1)14 = 1− 0.25× 0.3333 = 0.916675 = (.9167)1000

b(2)3 = b

(1)3 −m31b

(1)1 = 0− 0.25× 0 = 0 = (.0000)1000

m41 =a(1)41

a(1)11

=0.3333

2= 0.16665

a(2)42 = a

(1)42 −m41a

(1)12 = 0.5− 0.16665× 1 = 0.33335 = (.3334)1000

a(2)43 = a

(1)43 −m41a

(1)13 = 1− 0.16665× 0.5 = 0.916675 = (.9167)1000

a(2)44 = a

(1)44 −m41a

(1)14 = 0.5− 0.16665× 0.3333 = 0.44445 = (.4444)1000

b(2)4 = b

(1)4 −m41b

(1)1 = 0− 0.16665× 0 = 0 = (.0000)1000

k = 2:

(.2000)10+01 (.1000)10+01 (.5000)1000 (.3333)1000 (.0000)1000

(.0000)1000 (.5000)1000 (.7500)1000 (.3334)1000 (.1000)10+01

(.0000)1000 (.7500)1000 (.5417)1000 (.9167)1000 (.0000)1000

(.0000)1000 (.3334)1000 (.9167)1000 (.4444)1000 (.0000)1000

Trocar a 2.a linha com a 3.a linha:

(.2000)10+01 (.1000)10+01 (.5000)1000 (.3333)1000 (.0000)1000

(.0000)1000 (.7500)1000 (.5417)1000 (.9167)1000 (.0000)1000

(.0000)1000 (.5000)1000 (.7500)1000 (.3334)1000 (.1000)10+01

(.0000)1000 (.3334)1000 (.9167)1000 (.4444)1000 (.0000)1000

104 SEMANA 12

m32 =a(2)32

a(2)22

=0.50.75

= 0.6667

a(3)33 = a

(2)33 −m32a

(2)23 = 0.75− 0.6667× 0.5417 = 0.388884 = (.3888)1000

a(3)34 = a

(2)34 −m32a

(2)24 = 0.3334− 0.6667× 0.9167 = −0.27776 = −(.2778)1000

b(3)3 = b

(2)3 −m32b

(2)2 = 1− 0.6667× 0 = 1 = (.1000)10+01

m42 =a(2)42

a(2)22

=0.33340.75

= 0.4445

a(3)43 = a

(2)43 −m42a

(2)23 = 0.9167− 0.4445× 0.5417 = 0.67591 = (.6759)1000

a(3)44 = a

(2)44 −m42a

(2)24 = 0.4444− 0.4445× 0.9167 = 0.036926 = (.3693)10−01

b(3)4 = b

(2)4 −m42b

(2)2 = 0− 0.4445× 0 = 0 = (.0000)1000

k = 3:

(.2000)10+01 (.1000)10+01 (.5000)1000 (.3333)1000 (.0000)1000

(.0000)1000 (.7500)1000 (.5417)1000 (.9167)1000 (.0000)1000

(.0000)1000 (.0000)1000 (.3888)1000 −(.2778)1000 (.1000)10+01

(.0000)1000 (.0000)1000 (.6759)1000 (.3693)10−01 (.0000)1000

Trocar a 3.a linha com a 4.a linha:

(.2000)10+01 (.1000)10+01 (.5000)1000 (.3333)1000 (.0000)1000

(.0000)1000 (.7500)1000 (.5417)1000 (.9167)1000 (.0000)1000

(.0000)1000 (.0000)1000 (.6759)1000 (.3693)10−01 (.0000)1000

(.0000)1000 (.0000)1000 (.3888)1000 −(.2778)1000 (.1000)10+01


m43 =a(3)43

a(3)33

=0.38880.6759

= 0.5752

a(4)44 = a

(3)44 −m43a

(3)34 = −0.2778− 0.5752× 0.03693 = −0.29904 = −(.2990)1000

b(4)4 = b

(3)4 −m43b

(3)3 = 1− 0.5752× 0 = 1 = (.1000)10+01

O sistema condensado é dado por:

(.2000)10+01 (.1000)10+01 (.5000)1000 (.3333)1000

(.0000)1000 (.7500)1000 (.5417)1000 (.9167)1000

(.0000)1000 (.0000)1000 (.6759)1000 (.3693)10−01

(.0000)1000 (.0000)1000 (.0000)1000 −(.2990)1000

x1

x2

x3

x4

=

(.1000)1000

(.1000)1000

(.1000)1000

(.1000)10+01

Procedendo agora à substituição ascendente obtém-se:

−0.2990x4 = 1

⇔ x4 = −3.3444 = −(0.3344)10+01

0.6759x3 + 0.03693x4 = 0 ⇔ 0.6759x3 + 0.03693× (−3.3444) = 0

⇔ x3 = 0.18273 = (.1827)1000

0.75x2 + 0.5417x3 + 0.9167x4 = 0

⇔ 0.75x2 + 0.5417× 0.1827 + 0.9167× (−3.3444) = 0

⇔ x2 = 3.9557 = (.3956)10+01

2x1 + x2 + 0.5x3 + 0.3333x4 = 0

⇔ 2x1 + 3.956 + 0.5× 0.1827 + 0.3333× (−3.3444) = 0

⇔ x1 = −1.4663 = −(.1466)10+01

A solução do sistema de equações é:

x1

x2

x3

x4

=

−(.1466)10+01

+(.3956)10+01

+(.1827)1000

−(0.3344)10+01

¥Esta resolução ilustra o trabalho por vezes necessário para localizar um erro num

código que estejamos a programar. É pedido que se utilize a calculadora para asoperações elementares (processador) e se escrevesse os resultados em FP (memória).Em geral, estaremos a trabalhar com dois sistemas FP, um no cálculo e outro noregisto. ¡

13

TÓPICOS: Resolução de Sistemas de Equações Lineares (cont.): Mé-todos de factorização: método de Doolittle e Crout (Factorização LU); Método deCholeski (Factorização LLT ); Factorização LDLT ; Método de Doolittle e cálculo deinversa, determinante e número de condição de uma matriz.

LEITURAS RECOMENDADAS: Capítulo 6 (pp. 232-234 e 243–265) dolivro [Pina(1995)]


Métodos de Doolittle e Crout. Factorização LU

Repita o exercício 12.1 empregando agora em aritmética exacta o método da facto-rização triangular de Doolittle e de Crout, ou seja, resolva pelos métodos referidos oseguinte sistema de equações lineares:

x1 + x2 + x3 = 4

x1 − x2 + 2x3 = 4

2x1 + x2 + x3 = 5

CONCEITOS TEÓRICOS

Método de Doolittle: Factorizar LU com L de diagonal unitária.

Através do produto de matrizes — aqui ilustrado apenas para o caso de dimensãon = 3 — podem obter-se os coeficientes Lij e Uij com

1 0 0L21 1 0L31 L32 1

U11 U12 U13

0 U22 U23

0 0 U33

=

A11 A12 A13

A21 A22 A23

A31 A32 A33

,

108 SEMANA 13

de onde se obtém sucessivamente U11, L21 e L31; U12, U22 e L32; U13, U23 e U33,originando as seguintes expressões:

uij = aij −i−1∑m=1

limumj ; j ≥ i

lij =

(aij −

j−1∑m=1

limumj

)/ujj ; j < i

À sucessão de Uij e Lij indicada antes destas expressões, chamaremos varrimentopor colunas (em Doolittle).

Método de Crout: Factorizar LU com U de diagonal unitária.

Através do produto de matrizes — aqui ilustrado apenas para o caso de dimensãon = 3 — podem obter-se os coeficientes Lij e Uij com

L11 0 0L21 L22 0L31 L32 L33

1 U12 U13

0 1 U23

0 0 1

=

A11 A12 A13

A21 A22 A23

A31 A32 A33

,

de onde se obtém sucessivamente L11, U12 e U13; L21, L22 e U32; L31, L32 e U33,originando as seguintes expressões:

lij = aij −j−1∑m=1

limumj ; j 6 i

uij =

(aij −

i−1∑m=1

limumj

)/lii, j > i

À sucessão de Lij e Uij indicada antes destas expressões, chamaremos varrimentopor linhas (em Crout).

RESOLUÇÃO

O sistema de equações Ax = b é escrito na forma matricial:

1 1 11 −1 22 1 1

x1

x2

x3

=

445

.

Aplicando o método de Doolittle com o seu varrimento por colunas j = 1, 2, ..., n

tem-se:


Coluna 1 (j = 1):

ui1 = ai1, i 6 1

⇒ u11 = a11 ⇒ u11 = 1

li1 = ai1/u11, i > 1

⇒ li1 = ai1 ⇒ l21 = a21 = 1; l31 = a31 = 2

Coluna 2 (j = 2):

ui2 = ai2 −i−1∑m=1

limum2, i 6 2

⇒ u12 = a12 = 1; u22 = a22 − (l21u12) = −1− (1× 1) = −2

li2 =

(ai2 −

1∑m=1

limum2

)/u22, i > 2

⇒ l32 = (a32 − l31u12)/u22 =1− 2× 1−2

=12

Coluna 3 (j = 3):

ui3 = ai3 −i−1∑m=1

limum3, i 6 3

⇒ u13 = a13 = 1; u23 = a23 − (l21u13) = 2− (1× 1) = 1;

u33 = a33 − (l31u13 + l32u23) = 1−(

2× 1 +12× 1

)= −3

2

L =

1 0 01 1 02 1/2 1

e U =

1 1 10 −2 10 0 −3/2

Após a factorização de A = LU fazemos a substituição Ux = y e resolve-seprimeiro para y, i.e.:

Ax = b ⇔ (LU)x = b ⇔ L(Ux) = b ⇒

Ly = b

Ux = y

Faz-se a determinação de y resolvendo Ly = b:

1 0 01 1 02 1/2 1

y1

y2

y3

=

445

⇔ y =

40−3

110 SEMANA 13

seguido da determinação de x resolvendo Ux = y:

1 1 10 −2 10 0 −3/2

x1

x2

x3

=

40−3

⇔ x =

112

O vector x é a solução do sistema de equações.

====================================

Aplicando o método de Crout com o seu varrimento por linhas i = 1, 2, ..., n tem-se:

Linha 1 (i = 1):

l1j = a1j , j 6 1

⇒ l11 = a11 ⇒ l11 = 1

u1j = a1j/l11, j > 1

⇒ u1j = a1j ⇒ u12 = a12 = 1; u13 = a13 = 1

Linha 2 (i = 2):

l2j = a2j −j−1∑m=1

l2mumj , j 6 2

⇒ l21 = a21 = 1; l22 = a22 − (l21u12) = −1− (1× 1) = −2

u2j = (a2j − l21u1j) /l22, j > 2

⇒ u23 = (a23 − l21u13)/l22 =2− 1× 1−2

= −12

Linha 3 (i = 3):

l3j = a3j −j−1∑m=1

l3mumj , j 6 3

⇒ l31 = a31 = 2; l32 = a32 − (l31u12) = 1− (2× 1) = −1;

l33 = a33 − (l31u32 + l32u23) = 1−[2× 1 + (−1)×

(−1

2

)]= −3

2

L =

1 0 01 −2 02 −1 −3/2

e U =

1 1 10 1 −1/20 0 1


À semelhança do que efectuamos anteriormente, após a factorização de A = LU

fazemos

Ax = b ⇔ (LU)x = b ⇔ L(Ux) = b ⇒

Ly = b

Ux = y

A determinação de y faz-se resolvendo Ly = b:

1 0 01 −2 02 −1 −3/2

y1

y2

y3

=

445

⇔ y =

402

E, por fim, a determinação de x faz-se resolvendo Ux = y:

1 1 10 1 −1/20 0 1

x1

x2

x3

=

402

⇔ x =

112

O vector x é a solução do sistema de equações, que em aritmética exacta tem deser o mesmo que o obtido pelo método de Doolittle.

¥


Factorização LU. Cálculo do determinante

a) Calcule, em aritmética exacta, a factorização LU da matriz (com L unitária)

A =

1 0 9 00 9 0 05 0 0 50 1 0 3

b) Calcule o determinante de A a partir da factorização obtida.

CONCEITOS TEÓRICOS

Na resolução que se segue, da aplicação do método de condensação de Gaussobtém-se a factorização LU, onde L é uma matriz de diagonal unitária cujos res-tantes elementos não nulos são os coeficientes mij , sendo U a matriz resultante dacondensação (sem escolha de pivot).

Definição: O determinante de uma matriz A de dimensão n× n é obtido após afactorização de Gauss sem escolha de pivot fazendo:

detA = det(LU) = detL× detU =n∏

i=1

lii ×n∏

i=1

uii = 1×n∏

i=1

uii

pois L é uma matriz de diagonal unitária, isto é, lii = 1 para i = 1, . . . , n. ¤

112 SEMANA 13

RESOLUÇÃO

a) Condensação de Gauss:


k = 1:

1 0 9 00 9 0 05 0 0 50 1 0 3

m31 =a(1)31

a(1)11

=51

= 5

a(2)32 = a

(1)32 −m31a

(1)12 = 0− 5× 0 = 0

a(2)33 = a

(1)33 −m31a

(1)13 = 0− 5× 9 = −45

a(2)34 = a

(1)34 −m31a

(1)14 = 5− 5× 0 = 5

k = 2:

1 0 9 00 9 0 00 0 −45 50 1 0 3

m42 =a(2)42

a(2)22

=19

a(3)43 = a

(2)43 −m42a

(2)23 = 0− 1

9× 0 = 0

a(3)44 = a

(2)44 −m42a

(2)24 = 3− 1

9× 0 = 3

Obteve-se desta forma a factorização LU da matriz (com L unitária) dada pelasmatrizes:

U =

1 0 9 00 9 0 00 0 −45 50 0 0 3


e

L =

1 0 0 0m21 1 0 0m31 m32 1 0m41 m42 m43 1

=

1 0 0 00 1 0 05 0 1 00 1/9 0 1

.

b) O cálculo do determinante da matriz A é feito por:

detA = det(LU) = detL× detU = 1×4∏

i=1

uii

= 1× [1× 9× (−45)× 3] = −1215.

¥


Método de Choleski e factorização LDLT

a) Obtenha em aritmética exacta a factorização da matriz de Pascal para n = 3(aij : a1j = 1, ai1 = 1, aij = a(i−1)j + ai(j−1)), recorrendo ao método de Choleski.

b) Usando o resultado anterior, obtenha a factorização LDLT .

CONCEITOS TEÓRICOS

Método de Choleski: Factorizar LLT .

Através do produto de matrizes — aqui ilustrado apenas para o caso de dimensãon = 3 — podem obter-se os coeficientes Lij numa só etapa com:

L11 0 0L21 L22 0L31 L32 L33

L11 L12 L13

0 L22 L23

0 0 L33

=

A11 A12 A13

A21 A22 A23

A31 A32 A33

,

ou seja, calculando sucessivamente L11, L21 e L31; L22 e L32; L33 o que origina asseguintes expressões:

ljj =

(ajj −

j−1∑m=1

l2jm

)1/2

lij =

(aij −

j−1∑m=1

limljm

)/ljj , i > j ¤

De notar que se escolhe a raiz positiva.

À sucessão de Lij indicada antes destas expressões, chamaremos varrimento porcolunas (em Choleski).

114 SEMANA 13

RESOLUÇÃO

a) A matriz A é simétrica:

A =

1 1 11 2 31 3 6

.

Se fôr factorizável então é definida positiva. A sua factorização de Choleski éobtida em varrimento por colunas da seguinte forma:

Coluna 1 (j = 1)

l11 = (a11)1/2 = 1

l21 = a21/l11 = 1/1 = 1; l31 = a31/l11 = 1/1 = 1

Coluna 2 (j = 2)

l22 =(a22 − l221

)1/2= (2− 12)1/2 = 1

l32 = (a32 − l31l21) /l22 = (3− 1× 1)/1 = 2

Coluna 3 (j = 3)

l33 =[a33 −

(l231 + l232

)]1/2=

[6− (

12 + 22)]1/2

= 1

Obteve-se desta forma a factorização LLT da matriz, tal que:

L =

1 0 01 1 01 2 1

.

b) Como a diagonal de L é unitária não é preciso desenvolver o cálculo LDLT (ver13.4). A matriz D é a matriz identidade sendo a factorização dada pelas matrizes:

L =

1 0 01 1 01 2 1

, LT =

1 1 10 1 20 0 1

e D =

1 0 00 1 00 0 1

.

Notar que, em geral, após a aplicação do método de Choleski a matriz L resultantenão é de diagonal unitária. ¥



Método de Doolittle. Inversa, determinante e

número de condição

As matrizes de Pei (A) são definidas por: aii = c e aij = 1 para i 6= j com i, j =1, 2, . . . , n.

a) Obtenha a inversa e o determinante da matriz para n = 3 e c = 4 usando afactorização de Doolittle.

b) A matriz A da alinea a) é definida positiva, definida negativa ou indefinida?Justifique.

c) Calcule o número de condição dessa matriz (n = 3, c = 4) na norma de Frobe-nius. A matriz é bem condicionada? Justifique.

CONCEITOS TEÓRICOS

Norma de Frobenius de uma matriz A: Esta norma é dada por:

‖ A ‖F =

n∑

i,j=1

|aij |2

1/2

.

Número de condição e norma de Frobenius: cond A =‖ A ‖F × ‖ A−1 ‖F . ¤

RESOLUÇÃO

a) A matriz de Pei para n = 3 e c = 4 é

A =

4 1 11 4 11 1 4

.

Aplicando o método de Doolittle com varrimento por colunas tem-se:

Coluna 1 (j = 1):

ui1 = ai1, i 6 1

⇒ u11 = a11 ⇒ u11 = 4

li1 = ai1/u11, i > 1

⇒ li1 = ai1/4 ⇒ l21 = a21/4 =14; l31 = a31/4 =

14

116 SEMANA 13

Coluna 2 (j = 2):

ui2 = ai2 −i−1∑m=1

limum2, i 6 2

⇒ u12 = a12 = 1; u22 = a22 − (l21u12) = 4−(

14× 1

)=

154

li2 =

(ai2 −

1∑m=1

limum2

)/u22, i > 2

⇒ l32 = (a32 − l31u12)/u22 =1− 1

4 × 1154

=15

Coluna 3 (j = 3):

ui3 = ai3 −i−1∑m=1

limum3, i 6 3

⇒ u13 = a13 = 1; u23 = a23 − (l21u13) = 1−(

14× 1

)=

34;

u33 = a33 − (l31u13 + l32u23) = 4−(

14× 1 +

15× 3

4

)=

185

Obtém-se a seguinte factorização (com L de diagonal unitária)

L =

1 0 01/4 1 01/4 1/5 1

e U =

4 1 10 15/4 3/40 0 18/5

Cálculo da inversa A−1 da matriz A:

AA−1 = I

onde I é a matriz identidade.

Como A = LU, então

(LU)A−1 = I ⇔ L(UA−1) = I ⇒

Ly = I

UA−1 = Y

LY = I ⇔

1 0 01/4 1 01/4 1/5 1

y11 y12 y13

y12 y22 y23

y31 y32 y33

=

1 0 00 1 00 0 1

Y =

y11 y12 y13

y12 y22 y23

y31 y32 y33

=

1 0 0−1/4 1 0−1/5 −1/5 1


UA−1 = Y

⇔

4 1 10 15/4 3/40 0 18/5

a−111 a−1

12 a−113

a−112 a−1

22 a−123

a−131 a−1

32 a−133

=

1 0 0−1/4 1 0−1/5 −1/5 1

Portanto, a inversa é

A−1 =

a−111 a−1

12 a−113

a−112 a−1

22 a−123

a−131 a−1

32 a−133

=

+5/18 −1/18 −1/18−1/18 +5/18 −1/18−1/18 −1/18 +5/18

Determinante da matriz A (ver definição na p. 111):

detA = det(LU) = detL× detU = 1×3∏

i=1

uii

= 1×4×

>3

154× 18

5

= 54

b)

DU = D

L =

d11 0 00 d22 00 0 d33

1 u12 u13

0 1 u23

0 0 1

=

4 1 10 15/4 3/40 0 18/5

d11 = 4, d22 =154

d33 =185

b) A matriz é definida positiva uma vez que é possível factorizá-la e todos osvalores da matriz D são positivos.

c) Cálculo da norma de Frobenius da matriz A:

‖ A ‖F =

n∑

i,j=1

|aij |2

1/2

‖ A ‖F =(42 + 12 + 12 + 12 + 42 + 12 + 12 + 12 + 42

)1/2= 7.35

Cálculo da norma de Frobenius da matriz A−1:

‖ A−1 ‖F =

[3×

(+

518

)2

+ 6×(− 1

18

)2]1/2

= 0.5

Assim, cond A =‖ A ‖F × ‖ A−1 ‖F = 7.35× 0.50 = 3.67

118 SEMANA 13

Podemos concluir que a matriz A é bem condicionada, pois 3.67 é um númerorelativamente pequeno, isto é, da ordem de grandeza das unidades.

É este número que indica a maior, ou menor, influência que perturbações sobre aprecisão dos valores das entradas da matriz A e/ou do segundo membro b podem terna solução do sistema de equações associado (ver pp. 260 do livro [Pina(1995)]). ¥

REFERÊNCIAS

[Ferreira(1985)] Ferreira, J. C. Introdução À Análise Matemática. Fundação CalousteGulbenkian, Lisboa, 4.a edição, 1985.

[Pina(1995)] Pina, H. Métodos Numéricos. McGraw-Hill, Lisboa, 1995.

Friday, September 21, 2007 at 14:19

Colectanea exercicios

Documents

Transcript of Colectanea exercicios