Calculo numérico_Introducao

Transcript of Calculo numérico_Introducao

Calculo Numerico Introducao

Joao Paulo Gois

Universidade Federal do ABC

1

1Apresentacao baseada nos cursos

http://www2.icmc.usp.br/~alysson/wiki/pmwiki.php/Cursos/101SME301

http://www2.icmc.usp.br/~andretta/ensino/sme0300-2-12.html

http://www2.icmc.usp.br/~alysson/wiki/pmwiki.php/Cursos/101SME301http://www2.icmc.usp.br/~andretta/ensino/sme0300-2-12.html
Roteiro

Ementa

Motivacao

Bibliotecas Computacionais (C,C++, Fortran)

Programas
Ementa

Representacao Numerica no Computador;

Zero de Funcao;

Interpolacao Polinomial;

Sistemas Lineares (diretos e iterativos);

Metodo dos Mnimos Quadrados (Aproximacao);

Integracao Numerica.
Ementa


Zero de Funcao;




Ementa


Zero de Funcao;




Ementa


Zero de Funcao;




Ementa


Zero de Funcao;




Ementa


Zero de Funcao;




Ementa


Zero de Funcao;




Requisitos para o Curso de Calculo Numerico

Funcoes de uma variavel (FUV)

Nocoes de Programacao (PI, Bases Computacionais daCiencia)

Bases Matematicas

Material estara disponvel em nosso curso do TIDIA-AEhttp://tidia-ae.ufabc.edu.br

http://tidia-ae.ufabc.edu.br



Bases Matematicas





Bases Matematicas





Bases Matematicas





Bases Matematicas


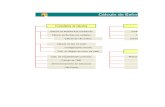
Modelando um Problema 08:51

Resoluo de um problema real

Adaptado de http://black.rc.unesp.br/balthazar/calculo/

Problema "real"

Idealizao (suposies)

Modelo matemtico

Tcnicas Matemticas

Resultado NumricoComparao

Experimentos

Resultados experimentais

ok ? FIM!
Metodos Numericos: os motivos

Problemas praticos sao (em geral) difceis de se resolverem;

ax2 + bx+ c = 0 (facil encontrar as razes);

cos(ax2) + sin(bx) + c = 0 (um pouco mais difcil);
Metodos Numericos: resolva o sistema linear

(1 21 1

)(xy

)=

(11

)

Sabemos que

A =(a bc d

) A1 = 1

det(A)

(d bc a

)Logo, (

xy

)=

(0.3333 . . .0.6666 . . .

)

(1 21 1

)(xy

)=

(11

)Sabemos que

A =(a bc d

) A1 = 1

det(A)

(d bc a

)

Logo, (xy

)=

(0.3333 . . .0.6666 . . .

)

(1 21 1

)(xy

)=

(11

)Sabemos que

A =(a bc d

) A1 = 1

det(A)

(d bc a

)Logo, (

xy

)=

(0.3333 . . .0.6666 . . .

)

A1010X101 = B101

A =

0.8147 0.1576 0.6557 0.7060 0.4387 0.2760 0.7513 0.8407 0.3517 0.07590.9058 0.9706 0.0357 0.0318 0.3816 0.6797 0.2551 0.2543 0.8308 0.05400.1270 0.9572 0.8491 0.2769 0.7655 0.6551 0.5060 0.8143 0.5853 0.53080.9134 0.4854 0.9340 0.0462 0.7952 0.1626 0.6991 0.2435 0.5497 0.77920.6324 0.8003 0.6787 0.0971 0.1869 0.1190 0.8909 0.9293 0.9172 0.93400.0975 0.1419 0.7577 0.8235 0.4898 0.4984 0.9593 0.3500 0.2858 0.12990.2785 0.4218 0.7431 0.6948 0.4456 0.9597 0.5472 0.1966 0.7572 0.56880.5469 0.9157 0.3922 0.3171 0.6463 0.3404 0.1386 0.2511 0.7537 0.46940.9575 0.7922 0.6555 0.9502 0.7094 0.5853 0.1493 0.6160 0.3804 0.01190.9649 0.9595 0.1712 0.0344 0.7547 0.2238 0.2575 0.4733 0.5678 0.3371

B =

0.16220.79430.31120.52850.16560.60200.26300.65410.68920.7482

Solucao:

X =

0.15491.12420.11120.35060.16000.28840.76940.88640.31210.3871
Aplicacoes do Calculo Numerico

Aprendemos analiticamente a calcular derivadas, integrais,encontrar razes (em alguns casos), resolver sistemas lineares;

Na pratica os dados sao gigantescos (matrizes de ordem demilhoes);

Modelos Matematicos envolvem equacoes complexas;

Solucoes inevitavelmente precisam ser numericas;
Programas

Matlab;

Scilab;

Octave;

Mathematica (Desktop/Browser)http://www.wolframalpha.com;

Maple

http://www.wolframalpha.com
Bibliotecas Computacionais

GNU Scientific Library (GSL) www.gnu.org/s/gsl/;

SuiteSparsehttp://www.cise.ufl.edu/research/sparse/SuiteSparse/;

PETsC http://www.mcs.anl.gov/petsc;

Bibliotecas CUDAhttp://www.nvidia.com/object/cuda_home_new.html

www.gnu.org/s/gsl/http://www.cise.ufl.edu/research/sparse/SuiteSparse/http://www.mcs.anl.gov/petschttp://www.nvidia.com/object/cuda_home_new.html
Exerccios

Faca em Matlab programas para calcular:

ex =

i=0

xn

n!(1)

sin(x) =

i=0

(1)n x2n+1

(2n+ 1)!(2)

cos(x) =

i=0

(1)n x2n

(2n)!(3)

As entradas sao x e o numero de termos da serie. Compare com oresultado dado pelo Matlab. Implemente tambem uma versao decada uma das series a seguir empregando como condicao de paradao erro relativo e o erro absoluto. OBS: Nao utilize funcoespre-definidas para se calcular exponencial ou fatorial. Utilizeapenas as operacoes basicas (+.-,*,/);
Livros
Referencias

BURDEN, Richard L; FAIRES, J Douglas. Analise numerica.[Numerical Analysis, 8 ed - EUA]. 2 ed. Sao Paulo: CengageLearning, c2008. xiii, 721 p. ISBN 9788522106011.

FRANCO, Neide Bertoldi. Calculo numerico. Sao Paulo:Pearson Prentice Hall, 2006. 505 p. ISBN 9798576050871

RUGGIERO, Marcia A. Gomes; LOPES, Vera Lucia da Rocha.Calculo numerico: aspectos teoricos e computacionais. 2 ed.Sao Paulo: Pearson Makron books, 1996. 406 p. ISBN9788534602044

CHAPMAN, Stephen J. Programacao em MATLAB paraengenheiros. Sao Paulo: Cengage Learning, 2009. 482 p.ISBN 8522103259

GILAT, Amos; SUBRAMANIAM, Vish. Numerical methodsfor engineers and scientists: an introduction with applicationsusing MATLAB. Hoboken, N.J: Wiley, c2008. xx, 459 p.Includes index. ISBN 9780471734406

Calculo numérico_Introducao

Documents

Transcript of Calculo numérico_Introducao