APLICAÇÕES TRIGONOMÉTRICAS EM …dspace.bc.uepb.edu.br/jspui/bitstream/123456789/476/1/PDF -...

0

UNIVERSIDADE ESTADUAL DA PARAIacuteBA CENTRO DE CIEcircNCIAS E TECNOLOGIA- CCT

DEPARTAMENTO DE MATEMAacuteTICA CURSO LICENCIATURA EM MATEMAacuteTICA

DJAVAN LUCENA REIS

APLICACcedilOtildeES TRIGONOMEacuteTRICAS EM TRIAcircNGULOS QUAISQUER

CAMPINA GRANDE-PB ABRIL DE 2011

1

DJAVAN LUCENA REIS


Trabalho de Conclusatildeo de Curso apresentado no Curso de Licenciatura Plena em Matemaacutetica da Universidade Estadual da Paraiacuteba em cumprimentos agraves exigecircncias para obtenccedilatildeo do Tiacutetulo de Licenciado em Matemaacutetica

Orientador Prof Ms Fernando Luiz Tavares da Silva

Campina GrandePB 2011

2

FICHA CATALOGRAacuteFICA ELABORADA PELA BIBLIOTECA CENTRAL ndash UEPB

R277d Reis Djavan Lucena

Aplicaccedilotildees trigonomeacutetricas em triacircngulos quaisquer [manuscrito] Djavan Lucena Reis ndash 2011

47 f il color Digitado Trabalho de Conclusatildeo de Curso (Graduaccedilatildeo em

Matemaacutetica) ndash Universidade Estadual da Paraiacuteba Centro de Ciecircncias Tecnoloacutegicas 2011

ldquoOrientaccedilatildeo Prof Me Fernando Luiz Tavares da Silva Departamento de Matemaacutetica e Estatiacutesticardquo

1 Geometria 2 Trigonometria 3 Matemaacutetica -

Triacircngulos I Tiacutetulo

21 ed CDD 516

3

DJAVAN LUCENA REIS


Trabalho de Conclusatildeo de Curso apresentado no Curso de Licenciatura Plena em Matemaacutetica da Universidade Estadual da Paraiacuteba em cumprimento agraves exigecircncias para obtenccedilatildeo do Tiacutetulo de Licenciado em Matemaacutetica

BANCA EXAMINADORA FERNANDO LUIS TAVARES DA SILVA_______________________ NOTA 85 Prof ( Orientador ndash UEPB) FRANCISCO DE SAacute RIBEIRO________________________________ NOTA 85 Prof (Examinador ndash UEPB)

ONILDO DOS REIS FREIRE_________________________ NOTA 85 Prof (Examinador ndash UEPB)

MEacuteDIA 85

4

Dedico este trabalho a todos os estudantes que

buscam compreender natildeo soacute a utilidade dos

triacircngulos como tambeacutem resolver problemas que

envolvem os mais diferentes tipos de triacircngulos

5

AGRADECIMENTOS

Agradeccedilo a Deus por ter me dado forccedilas e graccedila para enfrentar os desafios e superaacute-

los sem ele nada do que conquistei seria possiacutevel inclusive chegar ateacute esse momento

A minha famiacutelia que sempre foi agrave base da minha formaccedilatildeo e onde encontrei os

maiores incentivadores em todas as minhas investidas nas mais diversas aacutereas

A todos os professores que fazem o curso de matemaacutetica em especial agravequeles dos

quais fui aluno e tive o privileacutegio de partilhar de seus conhecimentos e amizade

Aos meus colegas de sala que juntamente comigo vivenciaram todos esses momentos

acadecircmicos com companheirismo e a todos o meus amigos que sempre acreditaram em mim

me incentivando sempre a prosseguir em cada desafio que se apresentasse a frente dos quais

posso citar para representa-los Livacircnia que sempre foi uma incentivadora e motivadora nas

minhas investidas

Ao meu Pastor Robeacuterio Ricardo incentivador muito especial e intercessor sempre

presente

A minha namorada Raquel que carinhosamente contribuiu na apresentaccedilatildeo desse

trabalho

Ao meu orientador pelas preciosas contribuiccedilotildees para a realizaccedilatildeo de meu trabalho

6

RESUMO

O presente trabalho eacute uma reflexatildeo sobre a importacircncia dos triacircngulos na vida

humana desde os tempos passados comeccedilando pela civilizaccedilatildeo egiacutepcia onde a Matemaacutetica

era essencialmente praacutetica e os triacircngulos deviam cumprir seu papel nesse contexto pelos

babilocircnicos que jaacute conheciam as relaccedilotildees entre os lados de um triacircngulo retacircngulo e a

civilizaccedilatildeo grega onde a matemaacutetica moderna se desenvolveu e atraveacutes de matemaacuteticos

gregos como Tales de Mileto outras propriedades dos triacircngulos ficaram conhecidas

Atualmente percebemos a importacircncia do triacircngulo em vaacuterias partes inuacutemeras construccedilotildees

levam em sua estrutura formatos de triacircngulos nos designes tudo para daacute uma maior

sustentaccedilatildeo eficiecircncia e beleza como eacute o caso dos Andaimes pontes triangulares velas de

barcos em formato triangular entre outras Embora hoje a trigonometria esteja presente em

vaacuterios ramos do conhecimento ela basicamente comeccedilou estudando as relaccedilotildees entre os

comprimentos dos lados de um triacircngulo retacircngulo e os acircngulos agudos formados por esse

triacircngulo Devido a necessidade de se estudarem triacircngulos que natildeo satildeo retacircngulos surgiram

algumas leis e teoremas que estabelecem relaccedilotildees em triacircngulos quaisquer como eacute caso da lei

dos senos e dos cossenos que nos permite calcular as medidas dos lados e acircngulos

desconhecidos O teorema da aacuterea por exemplo nos permite encontrar a aacuterea de um triacircngulo

qualquer em funccedilatildeo das medidas de dois lados desse triacircngulo e do acircngulo formado por

esses lados O conhecimento desses teoremas e leis nos proporciona desenvolver habilidades

que nos permitiraacute resolver problemas dos mais diversos que envolvam triacircngulos quaisquer e

que tenha um grau de dificuldade maior do que os que habitualmente encontramos nos livros

de ensino meacutedio e nos problemas propostos pelos professores de maneira geral

7

SUMAacuteRIO

RESUMO 06 INTRODUCcedilAtildeO 09 10 NOTAS HISTOacuteRICAS DA MATEMAacuteTICA 10

11 A MATEMAacuteTICA NO EGITO 10

12 A MATEMAacuteTICA DOS BABILOcircNICOS 12

13 A MATEMAacuteTICA GREGA 13

14 PITAacuteGORAS 14

15 NOTAS HISTOacuteRICAS DA TRIGONOMETRIA 15

151 A IMPORTAcircNCIA DOS TRIAcircNGULOS NA VIDA HUMANA 18

152 INFORMACcedilOtildeES BAacuteSICAS A RESPEITO DOS TRIAcircNGULOS 20

153 CONDICcedilAtildeO DE EXISTEcircNCIA DE UM TRIAcircNGULO 21

154 CONCEITO DE TRIAcircNGULO 22

155 TIPOS DE TRIAcircNGULOS 22

156 CURIOSIDADES A RESPEITO DO TRIAcircNGULO 23

16 GENERALIZACcedilAtildeO DO TEOREMA DE PITAacuteGORAS 24

161 FOacuteRMULAS E FORMAS DE SE OBTER A AacuteREA DE UM TRIAcircNGULO24

162 PROPRIEDADE DOS AcircNGULOS INTERNOS DO TRIAcircNGULO 26

163 PROPRIEDADE DO AcircNGULO EXTERNO DE UM TRIAcircNGULO 27

164 CRITEacuteRIOS DE CONGRUEcircNCIA DE TRIAcircNGULOS 28

17 CIacuteRCULO TRIGONOMEacuteTRICO 29

171 LINHAS TRIGONOMEacuteTRICAS 30

172 ESTUDO DO SINAL DO COSSENO E DO SENO 30

20 TRIGONOMETRIA EM TRIAcircNGULOS QUAISQUER 31

21 LEI DOS SENOS 31

22 LEI DOS COSSENOS 32

23 TEOREMA DA AacuteREA DE UM TRIAcircNGULO 34

24 PROJECcedilAtildeO ORTOGONAL35

8 30 APLICACcedilOtildeES 37

31 APLICACcedilOtildeES DO SENO 37

32 APLICACcedilOtildeES DO COSSENO 39

33 APLICACcedilOtildeES DO TEOREMA DA AacuteREA 41

34 APLICACcedilOtildeES DAS PROJECcedilOtildeES ORTOGONAIS 42

35 APLICACcedilOtildeES Agrave TOPOGRAFIA 43

CONSIDERACcedilOtildeES FINAIS 49

REFEREcircNCIAS BIBLIOGRAacuteFICAS 50

9

INTRODUCcedilAtildeO

A importacircncia dos triacircngulos na disciplina de Matemaacutetica eacute evidente isso porque

vaacuterios assuntos abordados em sala de aula podem ser explorados a partir de uma simples

observaccedilatildeo da estrutura do triacircngulo Podemos citar por exemplo acircngulos aacuterea periacutemetro e

casos de semelhanccedila que envolve a proacutepria figura A importacircncia do triacircngulo tambeacutem eacute

observaacutevel no nosso dia a dia pois devido a sua forma e equiliacutebrio que promove consistecircncia

eacute comum vermos edifiacutecios pontes paredes e estruturas quaisquer que fazem uso da forma

triangular por ela proporcionar mais seguranccedila e firmeza

A trigonometria que estuda basicamente as relaccedilotildees no triacircngulo eacute um dos assuntos

mais abordados dentro da disciplina de Matemaacutetica e muitas dessas relaccedilotildees trigonomeacutetricas

que satildeo vistas nas escolas satildeo relaccedilotildees que se datildeo principalmente no triacircngulo retacircngulo e

muitas vezes passam despercebido nas escolas outras relaccedilotildees que tambeacutem satildeo possiacuteveis de

ver em outros triacircngulos

Uma das propostas desse trabalho consiste ressaltar a importacircncia do triacircngulo

matemaacutetico com a apresentaccedilatildeo de algumas propriedades inerentes a figura e teoremas a ela

relacionados mas tambeacutem verificarmos que os triacircngulos estatildeo presentes no nosso dia a dia

sendo usados em nosso benefiacutecio

Poreacutem o objetivo maior desse trabalho eacute apresentar algumas aplicaccedilotildees

trigonomeacutetricas em triacircngulos quaisquer e para isso faremos uso de algumas demonstraccedilotildees

de leis tais como a do seno e cosseno que satildeo aplicaacuteveis aos mais diversos tipos de

triacircngulos

10 10 NOTAS HISTOacuteRICAS DA MATEMAacuteTICA

Desde a antiguidade o homem utiliza a matemaacutetica para facilitar a vida e organizar a

sociedade Na preacute-histoacuteria quando o homem era nocircmade e vivia em pequenos grupos vivendo

da caccedila e pesca esse periacuteodo foi marcado por um baixo niacutevel intelectual cientiacutefico e

matemaacutetico

Mas mesmo assim podemos citar algumas descobertas cientiacuteficas e matemaacuteticas

Neste periacuteodo houve a elaboraccedilatildeo de um processo rudimentar de contagem ranhuras em

ossos marcas em galhos desenhos em cavernas e pedras Tambeacutem podemos citar aqui o

processo que muitos utilizavam para relacionar quantidades ou seja para cada unidade

obtida era colocada uma pequena pedra em um saquinho Portanto boa parte dessas

descobertas matemaacutetica mencionadas derivam de ideacuteias que originalmente estavam centradas

nos conceitos de nuacutemero grandeza e forma1

Em certa eacutepoca pensou-se que a matemaacutetica estava ocupada apenas com os nossos

sentidos com aquilo que o homem podia perceber do mundo no qual vivia e foi apenas no

seacuteculo dezenove que a matemaacutetica pura se libertou das limitaccedilotildees sugeridas por observaccedilotildees

da natureza

Ao longo do tempo o homem a medida que ia se desenvolvendo tambeacutem ia

utilizando alguns conhecimentos que iriam facilitar sua vida em sociedade e a matemaacutetica

esteve presente na organizaccedilatildeo da vida social do homem Veremos mais adiante as principais

civilizaccedilotildees antigas que contribuiacuteram para o desenvolvimento dessa ciecircncia chamada

matemaacutetica

11 A MATEMAacuteTICA NO EGITO

A civilizaccedilatildeo egiacutepcia se desenvolveu ao longo de uma extensa faixa de terra feacutertil que

margeava o rio Nilo posiccedilatildeo geograacutefica que foi propiacutecia ao desenvolvimento da agricultura

base da economia no Egito Pelo fato de que a sociedade egiacutepcia era extremamente fixa e

centrada na pessoa do Faraoacute que natildeo permitia uma maior abertura para as classes inferiores

as ciecircncias foram prejudicadas mas mesmo assim houve algumas descobertas As construccedilotildees

das piracircmides datildeo a entender que o conhecimento matemaacutetico dos egiacutepcios era muito mais

avanccedilado que o conhecido nos papiros (ducumentos egiacutepcios em forma de uma estreita tira

1Boyer Carl B Histoacuteria da MatemaacuteticaRevista por Uta C Merzbach traduccedilatildeo Elza F GomideEdiccedilatildeo 2 editora Edgard blucher Satildeo Paulo1996(p1)

11 escritos na forma hieraacutetica que foram descobertos em escavaccedilotildees no Egito por volta do seacuteculo

XVIII dC) Estes papiros traziam uma seacuterie de problemas e coleccedilotildees matemaacuteticas em

linguagem hieraacutetica que forma um dos pilares da matemaacutetica grega a qual foi a base para

nossa matemaacutetica moderna isto em geometria e trigonometria Do ponto de vista matemaacutetico

os mais importantes satildeo os papiros de Moscou e os papiros de Rhind Nesse uacuteltimo por

exemplo continham problemas diversos onde satildeo aplicados os meacutetodos de divisatildeo e

multiplicaccedilatildeo dos egiacutepcios mostrando tambeacutem como eles empregavam a regra da falsa

posiccedilatildeo e muitos outros problemas matemaacuteticos voltados a questotildees praacuteticas Pode-se entatildeo

perceber que mesmo com todas as dificuldades e restriccedilotildees impostas pela forma de governo

houve um grande avanccedilo matemaacutetico e cientiacutefico no Egito2

Foi tambeacutem com o egiacutepcios que Comeccedilou- se tambeacutem com uma geometria elementar

e uma trigonometria baacutesica (esticadores de corda) para facilitar a demarcaccedilatildeo de terras Com

isso utilizaram-se os caacutelculos de aacutereas raiacutezes quadradas e fraccedilotildees Tambeacutem sabemos que os

egiacutepcios conheciam as relaccedilotildees meacutetricas em um triacircngulo retacircngulo

Outro registro matemaacutetico mais antigo ainda eacute o da numeraccedilatildeo hierogliacutefica egiacutepcia

que eram inscriccedilotildees sagradas feitas em tumbas e monumentos que foram decifradas e

descobriu-se que esse sistema de numeraccedilatildeo antigo baseava-se na escala dez Essa linguagem

simples utilizava siacutembolos diferentes para representar por exemplo a primeira duacutezia de

potecircncias dez um traccedilo vertical representava uma unidade um osso de calcanhar invertido

representava o nuacutemero 10 um laccedilo como uma letra C valia 100 um dedo dobrado valia

10000 e assim os egiacutepcios podiam expressar as primeiras noccedilotildees de quantidade3

A matemaacutetica egiacutepcia sempre foi essencialmente praacutetica Quando o rio Nilo estava no

periacuteodo das cheias comeccedilavam os problemas para as pessoas Para resolver estes problemas

foram desenvolvidos vaacuterios ramos da matemaacutetica Foram construiacutedas obras hidraacuteulicas

reservatoacuterios de aacutegua e canais de irrigaccedilatildeo no rio Nilo Aleacutem disso outras aacutereas do

conhecimento foram estudadas pelos egiacutepcios com o intuito de prever as cheias do rio Nilo

como eacute o caso da Astronomia

2 httpwwwsomatematicacombrhistoriaphp Acesso em 18042011 3 Boyer Carl B Histoacuteria da MatemaacuteticaRevista por Uta C Merzbach traduccedilatildeo Elza F GomideEdiccedilatildeo 2 editora Edgard blucher Satildeo Paulo1996(p7)

12 12 A MATEMAacuteTICA DOS BABILOcircNICOS

A Mesopotacircmia como tambeacutem eacute conhecida a Babilocircnia situava-se no oriente meacutedio

entre os rios Tigre e Eufrates onde hoje estaacute situado o Iraque e a Siacuteria principalmente Os

povos que formavam a Babilocircnia eram os Sumeacuterios Acaacutedios Amonitas Caldeus e Hititas A

ciecircncia e por conseguinte a matemaacutetica babilocircnica teve um grande desenvolvimento por parte

dos sacerdotes que detinham o saber nesta civilizaccedilatildeo A exemplo dos egiacutepcios os

babilocircnicos tinham uma ciecircncia e matemaacutetica extremamente praacutetica com o objetivo de

facilitar o caacutelculo do calendaacuterio a administraccedilatildeo das colheitas organizaccedilatildeo de obras puacuteblicas

e a cobranccedila de impostos bem como seus registros4

Os babilocircnicos tinham uma maior habilidade e facilidade de efetuar caacutelculos talvez

em virtude de sua linguagem ser mais acessiacutevel que a egiacutepcia Eles tinham teacutecnicas para

equaccedilotildees quadraacuteticas e bi ndash quadraacuteticas aleacutem de possuiacuterem foacutermulas para aacutereas de figuras

retiliacuteneas simples e foacutermulas para o caacutelculo de volume de soacutelidos simples Tambeacutem

conheciam as relaccedilotildees entre os lados de um triacircngulo retacircngulo e trigonometria baacutesica

conforme descrito na taacutebua ldquoPlimpton 322rdquo A numeraccedilatildeo posicional babilocircnica era

semelhante agrave egiacutepcia seguindo praticamente agraves mesmas regras para escrever os nuacutemeros

fazendo uso de repeticcedilotildees dos siacutembolos para representar unidades e dezenas poreacutem os

babilocircnicos perceberam que seus dois siacutembolos para unidades e dezenas bastavam para

representar qualquer inteiro por maior que fosse sem necessitar de uma excessiva repeticcedilatildeo

fazendo uso da notaccedilatildeo posicional isto eacute os babilocircnicos viram que seus siacutembolos podiam ter

funccedilatildeo dupla tripla ou em qualquer grau simplesmente recebendo valores que iam depender

somente de suas posiccedilotildees relativas na representaccedilatildeo de um nuacutemero Nosso nuacutemero 222 por

exemplo usa o algarismo 2 trecircs vezes com significados diferentes cada uma uma vez o 2

vale duas unidades depois vale 2 dezenas e por fim vale 2 centenas de modo anaacutelogo os

babilocircnicos fizeram uso muacuteltiplo de seus siacutembolos separando claramente os trecircs grupos de

duas cunhas cada e ai entendiam que o grupo da direita representava duas unidades o

segundo o dobro de sua base que era sessenta e o da esquerda o dobro do quadrado da base

esse numeral indicava 2(60)sup2 + 2(60) + 2 (ou 7322 em nossa notaccedilatildeo)5 Portanto esse sistema

posicional de base sexagesimal bem desenvolvido facilitava os caacutelculos e o trabalho com

4 wwwsomatematicacom acesso em 20042011 5 Boyer Carl B Histoacuteria da MatemaacuteticaRevista por Uta C Merzbach traduccedilatildeo Elza F GomideEdiccedilatildeo 2 editora Edgard blucher Satildeo Paulo1996(p18)

13 fraccedilotildees Por tudo isto que foi descrito a matemaacutetica babilocircnica eacute considerada mais

desenvolvida que a matemaacutetica egiacutepcia

13 A MATEMAacuteTICA GREGA

A civilizaccedilatildeo grega foi formada por muitos povos que se originaram da Europa e da

Aacutesia e eacute considerada por muitos o berccedilo da civilizaccedilatildeo ocidental A Greacutecia deu grande

contribuiccedilatildeo para a formaccedilatildeo da sociedade moderna em vaacuterias aacutereas tais como poliacutetica

avanccedilo comercial economia e claro contribuiccedilotildees dentro da ciecircncia e matemaacutetica A base da

revoluccedilatildeo matemaacutetica ocorrida na Greacutecia consistia basicamente na investigaccedilatildeo dos conceitos

matemaacuteticos isto eacute o porquecirc Enquanto a matemaacutetica egiacutepcia e babilocircnica se resumia em

saber como Com os gregos a matemaacutetica passou a ser voltada a conceituaccedilatildeo teoremas e

axiomas A matemaacutetica moderna teve origem no racionalismo grego e teve como principal

estimulador Tales de Mileto considerado o pai da matemaacutetica moderna Esse racionalismo

objetivou o estudo de quatro pontos fundamentais compreensatildeo do lugar do homem no

universo encontrar a ordem no caos ordenar as ideacuteias em sequecircncias loacutegicas e obtenccedilatildeo de

princiacutepios fundamentais

Com relaccedilatildeo a Tales de Mileto pouco se sabe sobre sua obra poreacutem segundo a

tradiccedilatildeo foi Tales quem primeiro explicou o eclipse solar ao verificar que a lua eacute iluminada

por esse astro Por esse e outros motivos Tales eacute considerado o primeiro dos Sete Saacutebios

Segundo a tradiccedilatildeo a proposiccedilatildeo conhecida como o teorema de Tales que diz que um acircngulo

inscrito num semiciacuterculo eacute um acircngulo reto pode ter sido aprendido por Tales em suas viagens

agrave Babilocircnia poreacutem a tradiccedilatildeo grega lhe atribui a demonstraccedilatildeo do teorema6 Outros quatro

teoremas tambeacutem tecircm suas demonstraccedilotildees atribuiacutedas a Tales satildeo eles

Um ciacuterculo eacute bissectado por um diacircmetro

Os acircngulos da base de um triacircngulo isoacutesceles satildeo iguais

Os pares de acircngulos opostos formados por duas retas que se cortam satildeo iguais

Se dois triacircngulos satildeo tais que dois acircngulos e um lado satildeo iguais respectivamente a

dois acircngulos e um lado de outro entatildeo os triacircngulos satildeo iguais

6 Boyer Carl B Histoacuteria da MatemaacuteticaRevista por Uta C Merzbach traduccedilatildeo Elza F GomideEdiccedilatildeo 2 editora Edgard blucher Satildeo Paulo1996(p32)

14 14 PITAacuteGORAS

Quando se trata de matemaacutetica natildeo poderiacuteamos deixar de mencionar outro grande

matemaacutetico grego da mesma eacutepoca de Tales de Mileto o famoso Pitaacutegoras matemaacutetico e

filoacutesofo grego nascido por volta de 570 aC na ilha de Samos na Greacutecia

Pitaacutegoras com 18 anos de idade jaacute dominava e conhecia vaacuterios ramos do

conhecimento matemaacutetico e filosoacutefico e foi estudando astronomia por exemplo que

Pitaacutegoras afirmou que o planeta terra era esfeacuterico e suspenso no espaccedilo Em umas de suas

visitas ao Egito desenvolveu o seu teorema mais famoso denominado Teorema de Pitaacutegoras

atraveacutes do qual pode-se encontrar a medida de qualquer lado de um triacircngulo retacircngulo

conhecendo-se os valores dos outros dois Acredita-se que ele desenvolveu esse teorema

depois que ficou encantado com as piracircmides do Egito

Pitaacutegoras fundou uma escola miacutestica voltada para a evoluccedilatildeo da matemaacutetica e

filosofia tendo como principais temas a harmonia matemaacutetica a doutrina dos nuacutemeros e o

dualismo coacutesmico O Siacutembolo da escola era um pentagrama que segundo Pitaacutegoras possuiacutea

algumas propriedades interessantes Podia se obter um pentagrama traccedilando as diagonais de

um pentaacutegono regular

Figura 1- Pitaacutegoras

Figura 2- pentagrama siacutembolo da escola Pitagoacuterica

Alguns estudiosos afirmam que Pitaacutegoras foi disciacutepulo de Tales mas isso eacute pouco

provaacutevel devido a diferenccedila de mais de um seacuteculo entre suas idades Embora eles tenham tido

algumas semelhanccedilas entre seus interesses de estudos Pitaacutegoras abordou a matemaacutetica de

forma diferente em seus estudos como o escritor Proclo afirma em sua obra geomeacutetrica de

Tales

Pitaacutegoras que veio depois dele transformou essa ciecircncia numa forma

liberal de instruccedilatildeo examinando seus princiacutepios desde o iniacutecio e investigando os

teoremas de modo imaterial e intelectual Descobriu a teoria das proporcionais e a

contruccedilatildeo de figuras coacutesmicas [Thomas 1939p149]

15

FIGURA 3 - Teorema mais famoso de Pitaacutegoras

15 NOTAS HISTOacuteRICAS DA TRIGONOMETRIA

A origem da trigonometria eacute incerta entretanto sabemos que o desenvolvimento da

mesma se deu principalmente devido aos problemas que ficaram sem soluccedilatildeo dentro da

astronomia geografia e navegaccedilatildeo Problemas esses que os egiacutepcios e babilocircnicos

procuraram solucionar aplicando conhecimentos da relaccedilatildeo entre os acircngulos e os lados de um

triacircngulo No antigo Egito eacute possiacutevel encontrar problemas relacionados com a construccedilatildeo das

piracircmides e que envolvem a cotangente referida no papiro de Rhind Podemos encontrar

tambeacutem uma taacutebua de secantes na taacutebua cuneiforme babilocircnica Plimpton 322

Um matemaacutetico que deu uma contribuiccedilatildeo significativa para a trigonometria foi

Ptolomeu (seacuteculo II) Na sua obra Almagesto composta de 13 livros conteacutem uma tabela de

cordas correspondentes a diversos acircngulos por ordem crescente de 0deg a 90deg com incremento

de 15rsquo e em funccedilatildeo da metade do acircngulo o que eacute equivalente a uma tabela de senos Contudo

foi Euller (seacutec XVIII) que ao usar invariavelmente o ciacuterculo de raio um introduziu o

conceito de seno de co-seno e de tangente como nuacutemeros bem como as notaccedilotildees atualmente

utilizadas7

7 httpwwwslidesharenetrobesulhistria-da-matemtica-2532508 Acesso em 24042011

16

Outros matemaacuteticos aleacutem desses jaacute citados deram uma grande contribuiccedilatildeo para o

desenvolvimento da trigonometria Exemplos que podemos citar Menelau de Alexandria

(responsaacutevel pelo teorema que diz que dois triacircngulos esfeacutericos satildeo congruentes se acircngulos

correspondentes satildeo iguais) Hiparco de Niceacuteia (responsaacutevel pela compilaccedilatildeo da primeira

tabela trigonomeacutetrica) Eratoacutestenes de Cirene (muito conhecido por precisar o tamanho da

terra atraveacutes de uma simples observaccedilatildeo solar em sua cidade) Aleacutem desses muitos outros

introduziram conhecimentos relacionados a trigonometria

Coube ao matemaacutetico Ptolomeu criar o ciacuterculo trigonomeacutetrico de 360 graus na

tentativa de associar valores numeacutericos agraves cordas num ciacuterculo que era a forma utilizada pelos

aacuterabes isto eacute os aacuterabes usaram linhas trigonomeacutetricas que funcionavam como cordas no

ciacuterculo Mas para Ptolomeu realizar tal proeza era preciso criar um esquema para subdividir

a circunferecircncia de um ciacuterculo e tambeacutem criar uma regra para subdividir o diacircmetro Sem

duacutevida foi o sistema sexagesimal que levou Ptolomeu a subdividir o diacircmetro do ciacuterculo

trigonomeacutetrico em 120 partes cada uma dessas partes ele subdividiu de novo em sessenta

minutos e cada minuto de comprimento em sessenta segundos Vejamos a figura abaixo

figura 4 ndash ciacuterculo trigonomeacutetrico

ArsquoA = eixo dos cossenos ( variando no intervalo real de -1 a +1)

BrsquoB = eixo dos senos ( variando no intervalo real de -1 a +1)

AT = eixo das tangentes ( variando no intervalo de menos infinito a mais infinito)

17

Atualmente a trigonometria natildeo se limita a estudar triacircngulos Encontramos aplicaccedilotildees

na mecacircnica eletricidade acuacutestica muacutesica astronomia engenharia medicina e etc Muitas

dessas aplicaccedilotildees envolvem conceitos que dificilmente lembram os triacircngulos que deram

origem agrave trigonometria como por exemplo

Haacute meacutetodos atuais de anaacutelise de medicina onde satildeo enviadas ondas ao coraccedilatildeo de

forma que efetuem interaccedilotildees seletivas com os tecidos a observar

Geodeacutesia estudo da forma e dimensatildeo da terra

Estudo da intensidade luminosa calcula-se a intensidade luminosa irradiada por uma

fonte luminosa para uma determinada regiatildeo

Em Geografia a trigonometria eacute usada para estimar distacircncias entre divisas8

Na Astronomia conhecimentos trigonomeacutetricos satildeo utilizados para calcular

aproximadamente as distacircncias entre as estrelas mais proacuteximas

Enfim vaacuterias ciecircncias aplicam conhecimentos trigonomeacutetricos para se desenvolver e

alcanccedilar resultados praacuteticos e precisos

Devemos reconhecer que os conhecimentos trigonomeacutetricos expandiram-se para as

mais diversas aacutereas do conhecimento dando sua devida contribuiccedilatildeo mas para fins de

estudos devemos retornar agrave origem da palavra trigonometria que significa medidas de

triacircngulo ou seja palavra originada do grego trigocircnom = triacircngulo + metron = medidas que

significa literalmente medidas de triacircngulo8

Como o proacuteprio significado da palavra trigonometria jaacute nos informa esse ramo da

matemaacutetica estuda os triacircngulos pode estudar particularmente os triacircngulos em um plano

onde um dos acircngulos eacute de 90deg isto eacute o triacircngulo retacircngulo Estuda tambeacutem as relaccedilotildees entre

os lados e os acircngulos dos triacircngulos Por isso eacute inegaacutevel a importacircncia dos triacircngulos natildeo

apenas para o estudo da trigonometria mas tambeacutem para os tempos atuais A seguir veremos

como o triacircngulo estaacute presente na nossa realidade e sua devida importacircncia para nossos dias

8httpptwikipediaorgwikiTrigonometria Acesso em 27042011

18 151 A IMPORTAcircNCIA DOS TRIAcircNGULOS NA VIDA HUMANA

Natildeo se pode afirmar com certeza quem inventou o triacircngulo ou como isso ocorreu

mas no passado algumas civilizaccedilotildees inventaram construccedilotildees que tinham a forma estrutural

de um triacircngulo Um exemplo que podemos citar eacute o caso da civilizaccedilatildeo grega nos seus

tempos primitivos usaram o triacircngulo de descarga construccedilatildeo que permitia descarregar

as pressotildees exercidas por grandes pesos que se encontravam por cima das portas dos tuacutemulos

e das cidadelas Devido ao peso as portas podiam abater mas com o triacircngulo o peso era

suportado por postes laterais que eram maciccedilos9

Na Idade Meacutedia surgiu tambeacutem uma vela triangular alinhada com o eixo longitudinal

do casco O uso dessa vela facilitou a navegaccedilatildeo pois anteriormente era usada uma vela

perpendicular ao eixo e de formato quadrado o que tornava a navegaccedilatildeo lenta

Figura 5 - Embarcaccedilatildeo usando vela de estrutura triangular

Na atualidade podemos identificar muitas situaccedilotildees em que se recorre a forma

triangular Muitos engenheiros usam com frequumlecircncia formas triangulares em suas construccedilotildees

para daacute estabilidade e seguranccedila as mesmas Observemos abaixo algumas situaccedilotildees em que

formas triangulares satildeo usadas

Figura 6 - Cobertura de Estaacutedio triangular

9 httpwwwprof2000ptuserssecjestemodtri01Pg000650htm Acesso em 29042011

19

Figura 7 - Ponte de ferro onde satildeo utilizadas formas

triangulares para daacute sustentaccedilatildeo a toda estrutura

Figura 8 - Para daacute mais sustentaccedilatildeo aos andaimes eles satildeo

triangularizados o que proporciona mais seguranccedila diminuindo os riscos de acidentes durante as construccedilotildees

Figura 9 - Passagens aeacutereas de estrutura triangular

Como podemos verificar estruturas triangulares estatildeo espalhadas ao nosso redor

dando formas a coisas que nos satildeo uacuteteis no dia a dia facilitando nossa vida A importacircncia

dos triacircngulos eacute evidente natildeo apenas nos estudos de mateacuterias que fazem uso dessa figura em

suas pesquisas mas tambeacutem porque os triacircngulos satildeo fundamentais para organizaccedilatildeo

estrutural de nossa sociedade no que diz respeito ao aspecto fiacutesico

20 152 INFORMACcedilOtildeES BAacuteSICAS A RESPEITO DO TRIAcircNGULO

Como jaacute foi dito anteriormente a palavra trigonometria significa medida dos lados de

um triacircngulo e atraveacutes do estudo da trigonometria podemos encontrar as medidas dos

elementos de um triacircngulo que satildeo os lados e os acircngulos Vale tambeacutem considerar que pelo

fato do estudo da trigonometria no seu iniacutecio se resumir ao estudo do triacircngulo eacute importante

termos conhecimentos baacutesicos sobre os triacircngulos conhecimentos esses que satildeo fundamentais

no estudo da trigonometria e que facilitam a resoluccedilatildeo de problemas do dia a dia

Na sequecircncia iremos apresentar algumas informaccedilotildees sobre os triacircngulos que satildeo

necessaacuterias para a introduccedilatildeo ao estudo da trigonometria

O triacircngulo eacute o uacutenico poliacutegono que natildeo possui diagonais

Cada um de seus acircngulos externos eacute suplementar do acircngulo externo adjacente

O periacutemetro de um triacircngulo eacute a soma das medidas de seus lados

A regiatildeo interna de um triacircngulo eacute chamada de regiatildeo convexa e a regiatildeo externa

chamada de regiatildeo cocircncava

A seguir veremos as condiccedilotildees necessaacuterias para que determinada figura seja

considerada um triacircngulo em seguida seratildeo apresentados os elementos de um triacircngulo e sua

classificaccedilatildeo tanto em relaccedilatildeo agraves medidas dos lados quantos as medidas dos acircngulos Outras

informaccedilotildees baacutesicas acerca dos triacircngulos aleacutem dessas citadas acima tambeacutem seratildeo

apresentadas tudo isso para facilitar o entendimento de algumas aplicaccedilotildees trigonomeacutetricas

nos triacircngulos diversos que seratildeo mostradas mais a frente

Vale considerar tambeacutem que tudo que seraacute informado sobre os triacircngulos sua

estrutura sua classificaccedilatildeo seus elementos e curiosidades natildeo satildeo apenas importantes para

compreensatildeo das demonstraccedilotildees e aplicaccedilotildees que seratildeo apresentadas nesse trabalho mas

tambeacutem satildeo essenciais para o aprendizado de conteuacutedos tanto na educaccedilatildeo baacutesica meacutedia

quanto na superior

21 153 CONDICcedilAtildeO DE EXISTEcircNCIA DE UM TRIAcircNGULO

Na construccedilatildeo de um triacircngulo observamos que a medida de qualquer um dos lados

do triacircngulo eacute menor que a soma das medidas dos outros dois e maior que o valor absoluto da

diferenccedila entre essas medidas Tal condiccedilatildeo eacute conhecida como Condiccedilatildeo de Existecircncia de um

Triacircngulo

Figura 10 - triacircngulo

| b - c | lt a lt b + c | a - c | lt b lt a + c | a - b | lt c lt a + b

Exemplo

Figura 11 ndash triacircngulo retacircngulo usado como exemplo

14 ndash 8 lt 10 lt 14 + 10 14 ndash 10 lt 8 lt 14 + 10 10 ndash 8 lt 14 lt 10 + 8

Podemos constatar no exemplo acima que todas as condiccedilotildees foram satisfeitas e

portanto podemos concluir que a figura acima eacute de fato um triacircngulo

22 154 CONCEITO DE TRIAcircNGULO

Triacircngulo eacute uma figura geomeacutetrica formada por trecircs retas que se encontram duas a

duas e natildeo passam pelo mesmo ponto formando trecircs lados e trecircs acircngulos

Observando o triacircngulo abaixo podemos identificar alguns de seus elementos

A B e C satildeo os veacutertices do triacircngulo

Os lados dos triacircngulos satildeo simbolizados pelos encontros dos veacutertices (pontos de

encontro) AB BC AC segmentos de retas

Os acircngulos tecircm duas formas de representaacute-los no caso do triacircngulo ele tem 3 lados

consequentemente 3 acircngulos Acirc B e Ĉ ou CBA BĈA BAcircC 155 TIPOS DE TRIAcircNGULOS

Com relaccedilatildeo aos lados os triacircngulos podem ser classificados em

Equumlilaacutetero Satildeo os triacircngulos que possuem os trecircs lados iguais

Isoacutesceles Satildeo os triacircngulos que possuem dois lados iguais

Escaleno Satildeo os triacircngulos que possuem os trecircs lados diferentes

Com relaccedilatildeo aos acircngulos internos os triacircngulos satildeo classificados em

Retacircngulo Satildeo aqueles que possuem um de seus acircngulos internos igual a 90deg

Obtusacircngulo Satildeo aqueles que possuem dois acircngulos agudos (menores que 90deg) e um acircngulo

obtuso (maior que 90deg)

Acutacircngulo Satildeo aqueles que possuem apenas acircngulos internos agudos (menores que 90deg)

23 155 CURIOSIDADES A RESPEITO DO TRIAcircNGULO

Fatos elementares sobre triacircngulos foram apresentados por Euclides em sua obra

denominada Os Elementos por volta de 300 aC Abaixo estatildeo algumas conclusotildees baacutesicas a

respeito do triacircngulo

O triacircngulo eacute um poliacutegono de trecircs lados

Dois triacircngulos satildeo ditos semelhantes se um pode ser obtido pela expansatildeo uniforme

do outro Este eacute o caso se e somente se seus acircngulos correspondentes satildeo iguais e isso

ocorre por exemplo quando dois triacircngulos compartilham um acircngulo e os lados opostos a

esse acircngulo O fato crucial sobre triacircngulos similares eacute que os comprimentos de seus lados satildeo

proporcionais Isto eacute se o maior lado de um triacircngulo eacute duas vezes o maior lado do triacircngulo

similar diz-se entatildeo que o menor lado seraacute tambeacutem duas vezes maior que o menor lado do

outro triacircngulo e o comprimento do lado meacutedio seraacute duas vezes o valor do lado

correspondente do outro triacircngulo Assim a razatildeo do maior lado e o menor lado do primeiro

triacircngulo seraacute a mesma razatildeo do maior lado e o menor lado do outro triacircngulo10

De acordo com o teorema angular de Tales a soma dos acircngulos internos de um

triacircngulo qualquer eacute igual a dois acircngulos retos (180deg ou ππππradianos) que nos permite

encontrar a medida do terceiro acircngulo uma vez conhecidas as medidas dos outros dois

acircngulos

Exemplo

Segundo um corolaacuterio do Teorema de Tales a medida de um acircngulo externo de um

triacircngulo eacute igual agrave soma das medidas dos acircngulos internos natildeo adjacentes

Outro teorema importante eacute o de Pitaacutegoras que afirma que em qualquer triacircngulo

retacircngulo o quadrado da medida da hipotenusa eacute igual agrave soma dos quadrados das medidas dos

outros dois lados Atraveacutes desse teorema podemos encontrar a medida de um dos lados do

triacircngulo desde que conheccedilamos a medida de dois de seus lados11

Figura 12 ndash triacircngulo Pitagoacuterico

10httprelebrandoamatematicablogspotcom201009calculo-da-area-do-triangulohtml acesso em 06052011 11 idem

24

16 GENERALIZACcedilAtildeO DO TEOREMA DE PITAacuteGORAS

O Teorema de Pitaacutegoras pode ser generalizado pela Lei dos Cossenos

csup2 = asup2 + bsup2 - 2 middot a middot b middot cos αααα

B

a c

C α b A

A lei dos cossenos pode ser aplicada a todos os triacircngulos mesmo se α natildeo for um

acircngulo reto Ele pode ser usado para ajudar a encontrar a medida dos lados e acircngulos de um

triacircngulo desde que as medidas de pelo menos dois lados e de um acircngulo interno sejam

conhecidas

161 FOacuteRMULAS E FORMAS DE SE OBTER A AacuteREA DE UM TRIAcircNGULO A aacuterea de um triacircngulo eacute a metade do produto da medida de sua altura pela medida de sua base Veja

A= 2

h) - b( onde

h eacute a altura do triacircngulo e ldquobrdquo e a medida da base Se o triacircngulo for equilaacutetero de lado ldquolrdquo sua aacuterea pode ser obtida pela foacutermula abaixo

A= 4

3lsup2

25

Podemos encontrar a aacuterea de um triacircngulo usando tambeacutem o Teorema de Heratildeo

atraveacutes da foacutermula do semi-periacutemetro a qual eacute

A = c) - (s b) - (s a) - (s s sdotsdotsdot onde 2

c b a s

++= eacute o semi-periacutemetro

Vejamos a demonstraccedilatildeo

Seja b a base do triacircngulo e h sua altura A aacuterea do triacircngulo eacute A = 2

h b

Pelo teorema dos cossenos sabemos que

csup2 = asup2 + bsup2 - 2abcos C = asup2 + bsup2 - 2b hsup2 - asup2 rArr hsup2 = asup2 - sup22b

csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b

csup2 - bsup2 asup2 - asup2 bsup2

+

= 16

csup2)sup2- bsup2 (asup2 - 2ab)sup2( + rArr

= 16

csup2))- bsup2 (asup2 csup2))(2ab- bsup2 (asup2 - (2ab +++=

16

csup2) - b)sup2 b)sup2)((a -(a - csup2( + rArr

= 16

c) b c)(a - b b)(a -a b)(c a - c( +++++= sc) - (sb) - (sa) - (s sdotsdotsdot

Portanto a aacuterea do triacircngulo pode ser dada pela seguinte foacutermula

A= c)-(sb) - (sa) - (ss sdotsdotsdot

26

Podemos achar a medida da aacuterea de um triacircngulo em funccedilatildeo da medida de dois lados

que conhecemos e do seno do acircngulo formado entre eles atraveacutes da foacutermula abaixo

A= 2

Acirc sen b c sdotsdot

Demonstraccedilatildeo Consideremos o triacircngulo abaixo

Sabemos que a aacuterea de um triacircngulo eacute dada por

A= 2

alturax base

rArrA = 2

h c sdot ( I )

Como o triacircngulo ACH eacute retacircngulo temos que

SenAcirc = b

hrArr senAcirc b h sdot= (II)

Substituindo (II) em (I) obtemos

A= 2

senAcirc b c sdotsdot

162 PROPREIDADE DOS AcircNGULOS INTERNOS DO TRIAcircNGULO

Essa propriedade afirma que a soma das amplitudes dos acircngulos internos de um

triacircngulo eacute igual a 180deg


27

Se construirmos mais 2 triacircngulos idecircnticos a o primeiro e giramos esses triacircngulos e

unindo-os de maneira que os acircngulos e θβα tornem-se dois a dois adjacentes como na

figura abaixo perceberemos que seraacute formado um acircngulo raso Observaccedilatildeo O acircngulo se torna

raso quando seus lados satildeo semi ndash retas opostas e a medida for de dois retos de 180deg

De onde concluiacutemos que deg=++ 180θβα 12

163 PROPRIEDADE DO AcircNGULO EXTERNO DE UM TRIAcircNGULO

Todo acircngulo externo de um triacircngulo eacute igual agrave soma das amplitudes dos dois acircngulos

internos natildeo adjacentes a ele Observe o triacircngulo e a consequente demonstraccedilatildeo

=α Acirc+ B

Demonstraccedilatildeo Da propriedade dos acircngulos internos sabemos que CBA ++ = 180deg No

entanto observe que α + C = 180degpois α e C satildeo acircngulos suplementares

Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA

12 httpeducacaouolcombrmatematicasoma-angulos-internos-triangulojhtm acesso em 10052011

28

164 CRITEacuteRIOS DE CONGRUEcircNCIA DE TRIAcircNGULOS

Para que dois triacircngulos sejam considerados congruentes eles devem obedecer alguns

criteacuterios Observe abaixo alguns casos de congruecircncia entre dois triacircngulos

1deg CASO Dois triacircngulos satildeo ditos congruentes se os trecircs lados de um for igual aos

trecircs lados do outro triacircngulo Esse caso eacute conhecido como LLL (lado lado lado)

TRIAcircNGULOS SEMELHANTES DO 1deg CASO

2deg CASO Dois triacircngulos satildeo iguais quando possuem dois lados iguais e o acircngulo

formado por eles satildeo iguais Caso conhecido como LAL (lado acircngulo lado)

TRIAcircNGULOS DO 2deg CASO DE SEMELHANCcedilA

3deg CASO Dois triacircngulos satildeo iguais se tecircm um lado igual e os dois acircngulos

adjacentes a esse lado satildeo iguais Esse eacute o caso LAA (ladoacircnguloacircngulo)


29

17 CIacuteRCULO TRIGONOMEacuteTRICO

Antes de iniciarmos qualquer demonstraccedilatildeo referente as leis do seno e cosseno ou

qualquer outro teorema relacionado a trigonometria faz-se necessaacuterio o estudo do ciacuterculo

trigonomeacutetrico Para entendermos as projeccedilotildees de um ponto qualquer pertencente ao ciacuterculo

nas coordenadas dos eixos sobre o qual a circunferecircncia encontra-se sobreposta dando

origem aos senos e cossenos de um acircngulo qualquer

O Ciacuterculo trigonomeacutetrico eacute um ciacuterculo de raio unitaacuterio cujo centro coincide com a

origem do sistema cartesiano

Figura 13 ndash ciacuterculo trigonomeacutetrico

Se considerarmos dois pontos A e B sobre o ciacuterculo trigonomeacutetrico de centro O e ligarmos a

esses dois pontos o centro O obteremos dois segmentos de reta OA e OB por sua vez o

par AO( OB ) define um acircngulo como podemos observar na figura abaixo


O ponto O eacute o veacutertice do acircngulo e os segmentos de retas OA e OB satildeo

respectivamente o lado origem e o lado extremidade

30 171 LINHAS TRIGONOMEacuteTRICAS

P eacute o ponto de intersecccedilatildeo do lado extremidade do acircngulo com o arco que limita o

ciacuterculo trigonomeacutetrico

O co-seno de αααα eacute a abcissa do ponto P

O seno de αααα eacute a ordenada do ponto P

C eacute o ponto de intersecccedilatildeo do lado extremidade do acircngulo com o eixo das tangentes

A tangente de αααα eacute a ordenada do ponto C

D eacute o ponto de intersecccedilatildeo do lado extremidade do acircngulo com o eixo das co-

tangentes

A cotg αααα eacute a abcissa do ponto C13

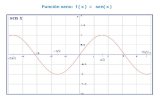
172 ESTUDO DO SINAL DO CO-SENO E DO SENO

Atraveacutes dos quadrantes abaixo veremos onde o cosseno e o seno de um acircngulo

assume valores positivos e negativos

-1 le sen α le 1 -1 le cos α le 1

13 httpwwweducfculpticmicm2000icm22circulo_trigonometricohtm Acesso em 20052011

31

Como podemos verificar nos ciacuterculos trigonomeacutetricos acima o seno de um acircngulo

assume valores positivos no 1deg e 2deg quadrantes e negativos nos 3deg e 4deg quadrantes Jaacute o co-

seno assume valores positivos no 1deg e 4deg quadrantes e negativos no 2deg e 3deg quadrantes

Todas as informaccedilotildees jaacute mencionadas nesse trabalho sobre os triacircngulos seus

componentes sobre o seno e o cosseno e o ciacuterculo trigonomeacutetrico seratildeo importantes no

decorrer desse trabalho nas demonstraccedilotildees que se seguiratildeo para uma maior compreensatildeo das

leis a serem vistas e de suas aplicaccedilotildees nos triacircngulos quaisquer que eacute nosso objetivo

principal

20 TRIGONOMETRIA EM TRIAcircNGULOS QUAISQUER

A partir de agora iremos tratar de algumas leis e teoremas matemaacuteticos que nos

ajudam a resolver problemas envolvendo triacircngulos quaisquer o que eacute justamente a proposta

desse trabalho Na sequumlecircncia traremos o enunciado das leis e teoremas com suas respectivas

demonstraccedilotildees e aplicaccedilotildees no sentido de alcanccedilar o objetivo de aplicar os conhecimentos

adquiridos com essas leis nos problemas que surgirem atingindo suas resoluccedilotildees

21 LEI DOS SENOS

Em qualquer triacircngulo o quociente entre cada lado e o seno do acircngulo eacute

constante e igual agrave medida do diacircmetro da circunferecircncia circunscrita ao triacircngulo

Demonstraccedilatildeo

Seja ABC um triacircngulo qualquer inscrito em uma circunferecircncia de raio R Por um

dos veacutertices do triacircngulo no caso o veacutertice B portanto de B trace um ponto diametralmente

oposto que chamaremos de D como podemos ver na figura a cima Em seguida ligando o

ponto C ao ponto D formando assim um novo triacircngulo BCD retacircngulo em C Observando a

figura gerada e sabendo que um acircngulo θ inscrito em uma circunferecircncia tem a metade do

valor do acircngulo central que subtende o mesmo arco na circunferecircncia (teorema do acircngulo

32

inscrito) podemos concluir que =Acirc D porque determinam na circunferecircncia uma

mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r

aDSen =rArrsdot=rArr=

De forma anaacuteloga se realizarmos esse mesmo processo para os acircngulos B e C

tambeacutem teremos as seguintes relaccedilotildees Bsen

b e

Csen

c= 2r onde b eacute a medida do lado AC

oposto a B c eacute a medida do lado AB oposto a C e 2r eacute uma constante Portanto podemos

concluir que

22 LEI DOS COSSENOS

Em qualquer triacircngulo o quadrado de um dos lados eacute igual agrave soma dos

quadrados dos outros dois lados menos o dobro do produto desses dois lados pelo

cosseno do acircngulo formado entre eles

1deg CASO ndash Seja ABC um triacircngulo com Acirc lt 90deg

Figura 16 ndash triacircngulo acutacircngulo

Considerando a figura acima podemos observar trecircs triacircngulos ABC BCD e BAD

Do triacircngulo BCD que eacute retacircngulo podemos extrair a seguinte relaccedilatildeo

asup2 = nsup2 + hsup2 ( I )

Do triacircngulo BAD que eacute retacircngulo temos

2rCsen

c

Bsen

b

Asen

a===

33

hsup2 = csup2 - msup2 ( II )

Ainda temos a seguinte relaccedilatildeo

n = b ndash m ( III )

substituindo as relaccedilotildees ( III ) e ( II ) em ( I ) temos

asup2 = (b ndash m)sup2 + csup2 - msup2 rarr asup2 = bsup2 + csup2 - 2bm

mas como no triacircngulo BAD m = c cos Acirc logo

Teremos que asup2 = bsup2 + csup2 -2bc cosAcirc

Da mesma forma pode-se demonstrar as demais relaccedilotildees

Bcos c a 2 - csup2 asup2 bsup2 sdotsdotsdot+=

Ccos b a 2 - bsup2 asup2 csup2 sdotsdotsdot+=

2deg CASO) Seja ABC um triacircngulo com 90deg lt Acirc lt 180deg

Figura 17 ndash triacircngulo obtusacircngulo

No triacircngulo BCH que eacute retacircngulo temos a seguinte relaccedilatildeo apoacutes aplicar o

teorema de Pitaacutegoras

asup2 = hsup2 + (x + c)sup2 = hsup2 + (csup2 + 2cx + xsup2) = (hsup2 + xsup2) + csup2 + 2cx ( I )

No triacircngulo AHC temos que bsup2 = hsup2 + xsup2 (II)

Temos tambeacutem que cos ( D ) = xb = cos (180deg- A) = -cos Acirc entatildeo x = - b cos Acirc (III)

Daiacute substituindo III e II em I e o valor de x teremos

asup2 = bsup2 + csup2 - 2bc cos Acirc

E estaacute demonstrada a lei do cosseno14

De forma anaacuteloga podemos provar as seguintes relaccedilotildees 14 Iezzi Gelson fundamentos de matemaacutetica elementar 3 trigonometria Ed Atual Editora LTDA Satildeo Paulo1996 ( p 227)

34

Bcos c a 2 - csup2asup2bsup2 sdotsdotsdot+= e Ccos b a 2 - bsup2asup2 csup2 sdotsdotsdot+=

A lei dos cossenos permite calcular o comprimento de um lado de qualquer triacircngulo

conhecendo o comprimento dos demais lados e a medida do acircngulo oposto a esse lado Essa

lei tambeacutem nos permite calcular a medida de todos os acircngulos de um triacircngulo desde que se

saiba o comprimento de todos os lados

23 TEOREMA DA AacuteREA DE UM TRIAcircNGULO

Teorema Em qualquer triacircngulo a aacuterea eacute igual ao semi-produto de dois lados

multiplicado pelo seno do acircngulo que eles formam


1deg caso) Seja ABC um triacircngulo com Acirc lt 90deg

C D ǀ-----------------------------------------------------------ǀ b

Vimos nas paacuteginas anteriores que a lei do Seno eacute expressa pelas seguintes expressotildees

2rCsen

c

Bsen

b

Asen

a=== essa lei nos permite deduzir uma foacutermula para aacuterea de um

triacircngulo qualquer

Sabemos que a aacuterea de um triacircngulo eacute igual ao produto da base pela altura dividido por

dois Entatildeo

At = 2

1middot basemiddot altura =

2

1middot a middot h

Perceba poreacutem que no triacircngulo retacircngulo ABD podemos escrever

SenAcirc = c

DB ou ainda DB = senAcirc middot c

Fazendo a substituiccedilatildeo dessa expressatildeo na foacutermula da aacuterea teremos

B c

A

a

35

At = 2

1 middot AC middot DB rArr At =

2

senAcirccb sdotsdot

2deg caso) Seja ABC um triacircngulo com 90deg lt Acirc lt 180deg

No triacircngulo AHC que eacute retacircngulo temos

CH = b sen (180deg - Acirc ) = b sen Acirc entatildeo

At = CH2

ABsdot =

2


E estaacute concluiacuteda a demonstraccedilatildeo desse Segundo caso15

De maneira anaacuteloga provamos tambeacutem que

At =2

Csenba sdotsdot ou At

2

Bsenca sdotsdot=

24 PROJECcedilAtildeO ORTOGONAL 1deg CASO TRIAcircNGULO ACUTAcircNGULO A c b B C ǀ -------------- a -----------------------ǀ

15 Iezzi Gelson fundamentos de matemaacutetica elementar 3 trigonometria Ed Atual Editora LTDA Satildeo Paulo1996 ( p 233)

36 Demonstraccedilatildeo

a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B

De maneira anaacuteloga segue que

b = acos C + ccos Acirc

c = bcos A + acos B

2deg CASO) TRIAcircNGULO OBTUSAcircNGULO A c b a D B C

DC = DB+ a

a = DC - DB

daiacute cos C = b

DC rArr DC = b cos C logo

Cos (180deg- B ) = c

DBrArr - cos B =

c

DBrArr DB= - cos B

Temos entatildeo que

a = bcos C - (- ccos )B rArr a = bcos C + ccos B

De maneira anaacuteloga obtemos

b = acos C + ccos B

e

c= acos B + bcos A

37 30 APLICACcedilOtildeES

Iremos a partir de agora vermos algumas aplicaccedilotildees do conteuacutedo visto neste trabalho

na resoluccedilatildeo de alguns problemas que envolvem triacircngulos quaisquer De preferecircncia

faremos uso da lei do seno lei do cosseno do teorema da aacuterea de um triacircngulo qualquer e da

projeccedilatildeo ortogonal com a finalidade de aprimorarmos o conhecimento acerca do assunto

mostrando aos leitores que eacute viaacutevel resolver problemas em triacircngulos que natildeo satildeo

retacircngulos o que eacute em suma a proposta desse trabalho

31 APLICACcedilOtildeES DA LEI DO SENO

Jaacute vimos anteriormente nas paacuteginas 32 e 33 deste trabalho a demonstraccedilatildeo da lei do

seno Veremos agora algumas situaccedilotildees problemas em que a aplicaccedilatildeo dessa lei nos

permitiraacute chega a sua soluccedilatildeo No entanto eacute importante sabermos quando eacute que devemos usar

a lei do seno para resolver determinada questatildeo Portanto devemos utilizar essa lei nas

situaccedilotildees em que temos um triacircngulo onde satildeo conhecidas as medidas de um lado e dois

acircngulos

1deg Aplicaccedilatildeo) Quais as medidas dos lados b e c na figura abaixo

A

C 45deg 15deg B

18

Soluccedilatildeo observando a figura percebemos que nos falta agrave medida de um dos acircngulos internos

do triacircngulo mas como jaacute sabemos pelo teorema dos 180deg que a soma dos acircngulos internos

de um triacircngulo eacute 180deg podemos facilmente encontrar a medida do acircngulo Acirc da seguinte

forma

deg=++ 180 C B A = deg=rArrdegdeg==deg=deg+deg+ 120A60 -180A1804515A

Podemos aplicar agora a lei dos senos que nos diz que

Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen

18 degsdot=degsdotrArr 15 sen 18 120 sen b = 537b

120 sen

15 sen18b congrArr

deg

degsdot=

Da mesma forma temos

38

15 sen

45 sen537c45 sen37515 senc

45 sen

c

45 sen

b

deg

degsdot==degsdot=degsdot=

deg=

degrArr

rArr 6914c86600

70710537c =rArr

sdot= E estaacute resolvido o problema

2deg Aplicaccedilatildeo) Observadores nos pontos A e B localizam um foco de incecircndio florestal no

ponto F Conhecendo os acircngulos FAcircB = 45deg e ABF = 30deg e a distacircncia AB = 15 km

Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b

Soluccedilatildeo como e exerciacutecio nos daacute apenas dois acircngulos e a medida de apenas um lado iremos

usar nesse caso a lei do seno

Temos entatildeo a seguinte relaccedilatildeo

F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg

Da igualdade iremos descobrir o valor do lado BF que chamaremos de ldquoardquo

30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=

Agora vamos descobrir o valor do lado ldquobrdquo Da igualdade anterior temos que

30sen105

b=

deg

Como natildeo temos o valor do seno de 105deg iremos decompor esse valor em dois

acircngulos cuja soma daacute 105deg satildeo eles os acircngulos 60deg e 45deg Daiacute usando uma foacutermula jaacute

conhecida iremos calcular o valor do seno de 105deg Vejamos

Sen (60deg + 45deg) = sen60deg cos45deg + sen45deg cos60deg

39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+

Como jaacute temos o valor do seno de 105deg substituiacutemos na relaccedilatildeo abaixo

30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km

32 APLICACcedilOtildeES DA LEI DO COSSENO

Essa lei do cosseno nos permite encontrar as medidas de todos os acircngulos desde que

Se saiba o comprimento de todos os lados do triacircngulo como jaacute pudemos ver na paacutegina 34

deste trabalho Veremos agora dois problemas envolvendo triacircngulos quaisquer que satildeo

facilmente resolvidos aplicando a lei do cosseno

1deg Aplicaccedilatildeo) Determine os acircngulos do triacircngulo abaixo cujos os lados medem 3 10 e 8

α 8 10 β γ 3 Soluccedilatildeo Aplicando a lei dos cossenos temos

3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40

Seguindo o mesmo raciociacutenio segue que

10sup2 = 3sup2 + 8sup2 -238cos β

100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27

minus=β 5620minusasymp

Para finalizar

8sup2 = 3sup2 + 10sup2 -2310cosγ

64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ

Portanto as medidas dos acircngulos seratildeo degcong 514α degcong 8123β e degcong 541γ

2deg Aplicaccedilatildeo) Os lados de um triacircngulo valem 3 4 e 6 Respectivamente o cosseno do maior

acircngulo interno desse triacircngulo vale

a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus

soluccedilatildeo Sabemos que num triacircngulo o maior lado fica oposto ao maior acircngulo Portanto

maior acircngulo seraacute oposto ao lado de medida 6 Sendo B e aplicando a lei do cosseno teremos

6sup2 = 3sup2 + 4sup2 -234cos B

36 = 9 + 16 -24cos B

-24cos B = 36 ndash 25

Portanto

cos B24

11minus= ( alternativa b )

41 33 APLICACcedilOtildeES DO TEOREMA DA AacuteREA

Sempre eacute comum encontrarmos nos livros de matemaacutetica do ensino fundamental ou do

meacutedio questotildees que pedem para achar a aacuterea de um triacircngulo e sempre que aparece a

medida de um acircngulo nesse triacircngulo os alunos sentem um pouco de dificuldade em saber

que foacutermula usar para resolver o problema No entanto o teorema da aacuterea demonstrado nas

paacuteginas 35 e 36 desse trabalho nos permite encontrar a aacuterea de qualquer triacircngulo

conhecendo dois lados de um triacircngulo e o acircngulo formado por eles Vejamos algumas

aplicaccedilotildees desse teorema

1degAplicaccedilatildeo) Dois lados de um triacircngulo medem 10cm e 20cm e formam entre si um acircngulo

de 30deg Qual a aacuterea desse triacircngulo

A

10 30deg

20

B

C

Soluccedilatildeo Perceba que a questatildeo nos daacute a medida de dois lados e esses lados formam

um acircngulo de 30deg o que corresponde ao primeiro caso do teorema da aacuterea que eacute quando o

acircngulo formado pelos lados eacute menor que 90deg Portanto ao aplicarmos na foacutermula teremos

At = senAcirccb2

1sdotsdotsdot degsdotsdotsdot= sen301020

2

1

At 5010202

1sdotsdotsdot= rArrAt = 50cmsup2

Logo a aacuterea desse triacircngulo eacute 50cmsup2

2degAplicaccedilatildeo) Um triacircngulo possui dois lados de medidas 20cm e 30cm que formam entre si

um acircngulo de 120deg Qual a aacuterea desse triacircngulo

A

20 c

D 120deg

H C 30 B

42

Soluccedilatildeo Perceba que o lado oposto ao acircngulo B eacute 20 logo b=20 e o lado oposto ao acircngulo

Acirc eacute 30 logo a=30

Notemos que o triacircngulo AHC eacute retacircngulo o que nos permite tirar a seguinte

conclusatildeo AH = b )C-sen(180 = b sen C entatildeo substituindo esta expressatildeo na foacutermula da

aacuterea de um triacircngulo obtemos

At = CsenAH2

CBsdotsdot =

2

sen1202030 degsdotsdot=

22

3600 sdot

= 150 3 cmsup2

Perceba que nesse problema tivemos que prolongar o lado CB para encontrarmos a

altura do triacircngulo e substituirmos posteriormente seu valor na foacutermula da aacuterea

34 APLICACcedilOtildeES DAS PROJECcedilOtildeES ORTOGONAIS

1deg Aplicaccedilatildeo) Encontre a medida do lado a do triacircngulo abaixo

A

30deg

10 20

30deg C

B a

Soluccedilatildeo Nesse triacircngulo note que temos a medida de um dos acircngulos internos maior que

90deg isto eacute o acircngulo B gt 90deg Como a questatildeo nos daacute a medida dos outros dois acircngulos

podemos encontrar a medida do acircngulo B pelo fato da medida dos acircngulos internos de um

triacircngulo ser 180deg De onde obtemos

deg=deg+deg+ 1803030B rArr B = 180deg - 60deg deg=rArr 120B

Como jaacute temos as medidas dos lados b e c e de seus respectivos acircngulos podemos

substituir seus valores na foacutermula abaixo para encontrarmos o lado que falta do triacircngulo

BccosCbcosa += degsdot+degsdot= cos12030cos3020 lembremos que o cos120deg eacute igual ao

cos60deg soacute que no segundo quadrante onde ele fica negativo o que nos daraacute

degsdotdegsdot= cos6030-cos3020a2

130

2

320 sdotminussdot= Portanto

15310a minus= cm

43

2degAplicaccedilatildeo) Dado o triacircngulo abaixo encontre a medida do lado b

B

8 10

45deg 30deg

A b C

Soluccedilatildeo Como conhecemos as medidas dos lados c e a e de seus respectivos acircngulos

podemos substituir seus valores diretamente na foacutermula das projeccedilotildees ortogonais do triacircngulo

ccosAcircCacosb += degsdot+degsdot= 45cos830cos102

28

2

310 sdot+sdot=

Portanto

2435b += cm

35 APLICACcedilOtildeES Agrave TOPOGRAFIA

A topografia eacute uma ciecircncia que estuda todos os acidentes geograacuteficos definindo a

situaccedilatildeo e a localizaccedilatildeo deles que podem ficar em qualquer lugar A topografia realiza a

anaacutelise das medidas de aacutereas e periacutemetros localizaccedilatildeo orientaccedilatildeo e analisa tambeacutem as

variaccedilotildees no relevo o que faz dessa ciecircncia um instrumento muito importante para a

implantaccedilatildeo e acompanhamento de obras como edificaccedilotildees urbanizaccedilatildeo e etc

Podemos portanto aplicar conhecimentos trigonomeacutetricos agrave topografia uma vez que

essa ciecircncia eacute aplicada em aacutereas pequenas da terra o que possibilita uma maior precisatildeo e

utilidade dessas aplicaccedilotildees A topografia portanto realiza tambeacutem caacutelculos de distacircncias que

natildeo podem ser medidas diretamente e o caacutelculo de distacircncias inacessiacuteveis onde satildeo aplicados

meacutetodos que utilizam conceitos de trigonometria A aplicaccedilatildeo desses meacutetodos necessita de um

instrumento capaz de medir acircngulos e que eacute muito utilizado por agrimensores topoacutegrafos e

engenheiros chamado de teodolito16 Esse aparelho nos mede acircngulos horizontais e verticais

com suas duas escalas circulares Com essas duas utilizaccedilotildees do teodolito podemos calcular

distacircncias inacessiacuteveis Vejamos a seguir duas aplicaccedilotildees trigonomeacutetricas agrave topografia

16 httpwwwcienciamaouspbrdadost2k_matematica_mat2g44arquivopdf Acesso em 28102011

44

1degAplicaccedilatildeo ) Realizar o Caacutelculo da distacircncia de um ponto acessiacutevel a um inacessiacutevel

Suponhamos que um observador situado num ponto A necessite medir a distacircncia desse

ponto a um ponto inacessiacutevel B poreacutem visiacutevel de A

Considere que o terreno seja plano nas imediaccedilotildees de A e que o observador adotaraacute o

seguinte procedimento

1deg) Escolheraacute um ponto C visiacutevel de A e de onde possa avistar B

2deg) Mediraacute entatildeo agrave distacircncia d entre os pontos A e C

3deg) Com um aparelho adequado colocado em a visaraacute os pontos B e C

4deg) Em seguida colocado em A visaraacute os pontos A e B determinando a medida do

acircngulo B

5deg) Com esses elementos calcularaacute AB

B

A α d β C

Em virtude da proporcionalidade entre os lados de um triacircngulo vista na lei do seno

podemos afirmar que

CBA sen

d

sen

AB=

β

Como CBA = 180deg - ( βα + ) temos )sen(

d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45

2degAplicaccedilatildeo) Caacutelculo da distacircncia de dois pontos inacessiacuteveis

Considere que um observador queira calcular a distacircncia de dois pontos A e B inacessiacuteveis

a ele Para isso adotaraacute o seguinte procedimento

1deg) O observador escolheraacute entatildeo dois pontos C e D dos quais possa avistar A e B

2deg) Mediraacute a distacircncia d entre esses pontos

3deg) Com um aparelho adequado colocado em C e posteriormente em D mediraacute os

acircngulos γβα e δ

Desta forma ficam determinados os triacircngulos ACD e BCD

A

B α δ D β γ C

Os lados AB e CD satildeo facilmente calculados pelas foacutermulas abaixo

AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot

Conhecidos os lados AD e BD do triacircngulo ABD e o acircngulo δ pode-se determinar

AB atraveacutes da Lei dos Senos

Podemos verificar nessas aplicaccedilotildees que eacute muito comum o uso de expressotildees

trigonomeacutetricas para realizar caacutelculos de medidas distacircncias entre pontos acessiacuteveis ou natildeo

caacutelculo de aacutereas ou periacutemetros entre outras mediccedilotildees o que deixa claro a importacircncia da

trigonometria em nossos dias e o quanto as aplicaccedilotildees de seus conceitos e relaccedilotildees satildeo

essenciais para nossos dias sendo possiacutevel portanto verificar seus benefiacutecios

46

CONSIDERACcedilOtildeES FINAIS

Na atualidade a figura do triacircngulo assume um papel muito importante na vida da

populaccedilatildeo e essa importacircncia natildeo estaacute restrita apenas agrave sala de aula onde conhecimentos satildeo

adquiridos atraveacutes da abordagem de assuntos que envolvem triacircngulos assuntos esses que

satildeo vistos desde o ensino fundamental ateacute o ensino superior Hoje eacute comum engenheiros

recorrerem agraves formas triangulares para daacute maior seguranccedila as suas construccedilotildees podemos ver

constantemente andaimes triangularizados sendo usados nas construccedilotildees civis postes de alta

tensatildeo e guindastes que usam formas triangulares tudo para proporcionar seguranccedila e

eficiecircncia nas construccedilotildees

Verdade tambeacutem que falar de triacircngulos e natildeo falar de trigonometria consistiria em

um grande erro uma vez que esse conhecimento matemaacutetico estuda as relaccedilotildees existentes em

um triacircngulo Hoje a trigonometria tem muitas aplicaccedilotildees tanto na matemaacutetica pura quanto

na matemaacutetica aplicada e consequentemente nas ciecircncias naturais o que vem apenas

confirmar o quanto esse ramo do conhecimento eacute importante

Como pudemos ver nesse trabalho as relaccedilotildees trigonomeacutetricas nos triacircngulos sejam

eles quais forem nos permite obter foacutermulas que iraacute nos auxiliar na resoluccedilatildeo de questotildees que

envolvem triacircngulos pois essas foacutermulas obtidas lei do seno lei do cosseno aleacutem do

teorema da aacuterea e as projeccedilotildees ortogonais no triacircngulo tem por finalidade relacionar os

acircngulos do triacircngulo com as medidas dos lados o que nos ajuda a resolver problemas diversos

em triacircngulos quaisquer

Podemos perceber que as relaccedilotildees existentes no triacircngulo podem ser de faacutecil

compreensatildeo e aplicaccedilatildeo se forem bem trabalhadas em sala de aula e exploradas com

dedicaccedilatildeo o que possibilitaraacute ao estudante perceber quando e em que situaccedilatildeo deve-se

aplicar cada relaccedilatildeo vista neste trabalho como eacute o caso da lei do cosseno onde podemos

encontrar a medida de um dos lados dos triacircngulo em funccedilatildeo dos outros dois e do acircngulo

formado entre eles e assim por diante

Quando trabalhamos com triacircngulo retacircngulo os alunos tem grande facilidade de

entender as relaccedilotildees existentes achar medidas dos lados e dos acircngulos desse triacircngulo e etc

graccedilas ao teorema do grande Pitaacutegoras mas quando passamos a trabalhar com triacircngulos

quaisquer a facilidade jaacute natildeo eacute a mesma por isso procuramos ver e estabelecer novas relaccedilotildees

que podem ser obtidas de qualquer triacircngulo o que pode ser uma ferramenta a mais para o

aluno que deseja melhorar seus conhecimentos em trigonometria e saber aplicar esses

conhecimentos em outras aacutereas como por exemplo na topografia encontrando distacircncias

47

REFEREcircNCIAS BIBLIOGRAacuteFICAS Boyer Carl B Histoacuteria da MatemaacuteticaRevista por Uta C Merzbach traduccedilatildeo Elza F GomideEdiccedilatildeo 2 editora Edgard blucher Satildeo Paulo1996 Iezzi Gelson fundamentos de matemaacutetica elementar 3 trigonometria Ed Atual Editora LTDA Satildeo Paulo1996 Monteiro H Jacy Boulos Paulo Watanabe Renate Matemaacutetica 1 para os cursos de 2deg grau Editora Nacional S A Satildeo Paulo1975

SITES CITADOS httpwwwsomatematicacombrhistoriaphp Acesso em 18042011 wwwsomatematicacom Acesso em 20042011 httpwwwslidesharenetrobesulhistria-da-matemtica-2532508 Acesso em 24042011 httpptwikipediaorgwikiTrigonometria Acesso em 27042011

httpwwwprof2000ptuserssecjestemodtri01Pg000650htm Acesso em 29042011 httprelebrandoamatematicablogspotcom201009calculo-da-area-do-triangulohtml Acesso em 06052011 httpeducacaouolcombrmatematicasoma-angulos-internos-triangulojhtm Acesso em 10052011 httpwwweducfculpticmicm2000icm22circulo_trigonometricohtm Acesso em 25072011 httpwwwcienciamaouspbrdadost2k_matematica_mat2g44arquivopdf Acesso em 28112011

1

DJAVAN LUCENA REIS


Trabalho de Conclusatildeo de Curso apresentado no Curso de Licenciatura Plena em Matemaacutetica da Universidade Estadual da Paraiacuteba em cumprimentos agraves exigecircncias para obtenccedilatildeo do Tiacutetulo de Licenciado em Matemaacutetica

Orientador Prof Ms Fernando Luiz Tavares da Silva

Campina GrandePB 2011

2









21 ed CDD 516

3

DJAVAN LUCENA REIS





MEacuteDIA 85

4





5

AGRADECIMENTOS











minhas investidas


presente


trabalho


6

RESUMO






















7

SUMAacuteRIO






















21 LEI DOS SENOS 31












9





















triacircngulos





matemaacutetico











da natureza





matemaacutetica






















































































































Tales





15
















utilizadas7


16




















17













































19



































quanto na superior





Triacircngulo



Exemplo








































acircngulos

Exemplo









24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




2









21 ed CDD 516

3

DJAVAN LUCENA REIS





MEacuteDIA 85

4





5

AGRADECIMENTOS











minhas investidas


presente


trabalho


6

RESUMO






















7

SUMAacuteRIO






















21 LEI DOS SENOS 31












9





















triacircngulos





matemaacutetico











da natureza





matemaacutetica






















































































































Tales





15
















utilizadas7


16




















17













































19



































quanto na superior





Triacircngulo



Exemplo








































acircngulos

Exemplo









24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




3

DJAVAN LUCENA REIS





MEacuteDIA 85

4





5

AGRADECIMENTOS











minhas investidas


presente


trabalho


6

RESUMO






















7

SUMAacuteRIO






















21 LEI DOS SENOS 31












9





















triacircngulos





matemaacutetico











da natureza





matemaacutetica






















































































































Tales





15
















utilizadas7


16




















17













































19



































quanto na superior





Triacircngulo



Exemplo








































acircngulos

Exemplo









24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




4





5

AGRADECIMENTOS











minhas investidas


presente


trabalho


6

RESUMO






















7

SUMAacuteRIO






















21 LEI DOS SENOS 31












9





















triacircngulos





matemaacutetico











da natureza





matemaacutetica






















































































































Tales





15
















utilizadas7


16




















17













































19



































quanto na superior





Triacircngulo



Exemplo








































acircngulos

Exemplo









24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




5

AGRADECIMENTOS











minhas investidas


presente


trabalho


6

RESUMO






















7

SUMAacuteRIO






















21 LEI DOS SENOS 31












9





















triacircngulos





matemaacutetico











da natureza





matemaacutetica






















































































































Tales





15
















utilizadas7


16




















17













































19



































quanto na superior





Triacircngulo



Exemplo








































acircngulos

Exemplo









24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




6

RESUMO






















7

SUMAacuteRIO






















21 LEI DOS SENOS 31












9





















triacircngulos





matemaacutetico











da natureza





matemaacutetica






















































































































Tales





15
















utilizadas7


16




















17













































19



































quanto na superior





Triacircngulo



Exemplo








































acircngulos

Exemplo









24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




7

SUMAacuteRIO






















21 LEI DOS SENOS 31












9





















triacircngulos





matemaacutetico











da natureza





matemaacutetica






















































































































Tales





15
















utilizadas7


16




















17













































19



































quanto na superior





Triacircngulo



Exemplo








































acircngulos

Exemplo









24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47












9





















triacircngulos





matemaacutetico











da natureza





matemaacutetica






















































































































Tales





15
















utilizadas7


16




















17













































19



































quanto na superior





Triacircngulo



Exemplo








































acircngulos

Exemplo









24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47








matemaacutetico











da natureza





matemaacutetica






















































































































Tales





15
















utilizadas7


16




















17













































19



































quanto na superior





Triacircngulo



Exemplo








































acircngulos

Exemplo









24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47
















































































































Tales





15
















utilizadas7


16




















17













































19



































quanto na superior





Triacircngulo



Exemplo








































acircngulos

Exemplo









24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




15
















utilizadas7


16




















17













































19



































quanto na superior





Triacircngulo



Exemplo








































acircngulos

Exemplo









24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




16




















17













































19



































quanto na superior





Triacircngulo



Exemplo








































acircngulos

Exemplo









24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




17













































19



































quanto na superior





Triacircngulo



Exemplo








































acircngulos

Exemplo









24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47






















19



































quanto na superior





Triacircngulo



Exemplo








































acircngulos

Exemplo









24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




























quanto na superior





Triacircngulo



Exemplo








































acircngulos

Exemplo









24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47








Triacircngulo



Exemplo








































acircngulos

Exemplo









24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47







































acircngulos

Exemplo









24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




24




B

a c

C α b A




conhecidas


A= 2

h) - b( onde


A= 4

3lsup2

25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




25




c b a s




h b



csup2- bsup2 asup2

+ Assim

Asup2 = 4

hsup2bsup2 sdot=

4

sup22b


+

= 16


= 16


16


= 16




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




26



A= 2




A= 2

alturax base

rArrA = 2

h c sdot ( I )


SenAcirc = b



A= 2






27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




27









=α Acirc+ B



Daiacute segue que

CBA ++ = C+α

Portanto

α=+ BA


28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




28













29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




29
























tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47












tangentes







31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




31








principal







21 LEI DOS SENOS










32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




32


mesma corda BC

Temos entatildeo

2rsenAcirc

asenAcirc 2ra

2r




b e

Csen



concluir que

22 LEI DOS COSSENOS










2rCsen

c

Bsen

b

Asen

a===

33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




33






















34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




34











C D ǀ-----------------------------------------------------------ǀ b


2rCsen

c

Bsen

b

Asen




dois Entatildeo

At = 2


2

1middot a middot h


SenAcirc = c



B c

A

a

35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




35

At = 2


2

senAcirccb sdotsdot




At = CH2

ABsdot =

2




At =2


2

Bsenca sdotsdot=




a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47





a = BD + DC

Cos B = c

BDrArr BD = c cos B

Cos C = b

DCrArr DC = b cos C

Daiacute temos

a = bcos C + ccos B



c = bcos A + acos B


DC = DB+ a

a = DC - DB

daiacute cos C = b



DBrArr - cos B =

c

DBrArr DB= - cos B




b = acos C + ccos B

e

c= acos B + bcos A














acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47

















acircngulos


A

C 45deg 15deg B

18




forma



Csen

c

Bsen

b

Asen

a==

deg=

deg 15 sen

b

120 sen


120 sen

15 sen18b congrArr

deg

degsdot=


38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




38

15 sen


45 sen

c

45 sen

b

deg


deg=

degrArr

rArr 6914c86600

70710537c =rArr




Determine AF e BF

B

15km 105deg a

A 45deg 30deg F

b




F sen

f

B sen

b

Acirc sen

a== =

deg=

deg=

deg sen30

15

sen105

b

sen45

a

Teremos entatildeo

2

115

sen105

b

sen45

a=

deg=

deg= 30

sen105

b

45 sen

a=

deg=

deg


30sen45

a=

deg= km 215a30

2

2a30

2

2

a=rArrsdot=rArr=


30sen105

b=

deg





39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




39

Sen (105deg) = 2

3

2

1

2

2

2

2sdot+sdot

Sen (105deg) = 4

26

4

2

4

6 +=+


30sen105

b=

deg= 30

4

26

b=

+=

4

2630b

+sdot=

+sdot==

2

2615b

Portanto

( )2675b +sdot= km








3sup2 = 10sup2 + 8sup2 - 2108 cosα

9 = 100 + 64 ndash 160 cosα

cosα = 160

155

minus

minuscong 0968

40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




40



100 = 9 + 64 -48cos β

-48cos β = 100 - 73

cos48

27


Para finalizar


64 = 9 + 100 ndash 60cosγ

- 60cosγ 45minus=

cos 75060

45cong

minus

minus=γ




a) 24

11 b)

24

11minus c)

8

3 d)

8

3minus e)

10

3minus




36 = 9 + 16 -24cos B


Portanto

cos B24












A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47














A

10 30deg

20

B

C




At = senAcirccb2


2

1

At 5010202





A

20 c

D 120deg

H C 30 B

42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




42






At = CsenAH2

CBsdotsdot =

2


22

3600 sdot

= 150 3 cmsup2





A

30deg

10 20

30deg C

B a











130

2


15310a minus= cm

43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




43


B

8 10

45deg 30deg

A b C




28

2

310 sdot+sdot=

Portanto

2435b += cm

















44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




44










acircngulo B


B

A α d β C


podemos afirmar que

CBA sen

d

sen

AB=

β


d

B sen

AB

βα +=

AB =)sen(

sen d

βα

β

+

sdot

45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




45









A

B α δ D β γ C


AC)sen(

)sen(d

δβα

βα

++

+sdot= e BC =

)sen(

)sen(d

δγβ

βα

++

+sdot








46


































47




46


































47




47




APLICAÇÕES TRIGONOMÉTRICAS EM …dspace.bc.uepb.edu.br/jspui/bitstream/123456789/476/1/PDF -...

Documents

Transcript of APLICAÇÕES TRIGONOMÉTRICAS EM …dspace.bc.uepb.edu.br/jspui/bitstream/123456789/476/1/PDF -...