3

2. Método de Monte Carlo

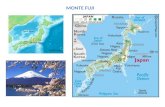
O método de Monte Carlo é uma denominação genérica tendo em comum o uso de variáveis aleatórias para resolver, via simulação numérica, uma variada gama de problemas matemáticos. Monte Carlo é uma localidade de Mônaco (figura 2.1), cidade estado encravada no sul da França conhecida pelos cassinos e os jogos de azar, que são exemplos típicos de sorteios cujos resultados são números ou eventos aleatórios.

Figura 2.1:

Mônaco, cidade estado famosa pelos cassinos.

O método popularizou-se com os computadores modernos e os programas geradores de números aleatórios. Na realidade são denominados números pseudoaleatórios, uma vez que são gerados por algoritmos numéricos, sequencialmente, a partir de um número inicial, resultando numa distribuição uniforme de números entre 0 e 1, inclusive, e que devem satisfazer a critérios de aleatoriedade.

Figura 2.2:

Mapa da região

onde se localiza o principado de Mônaco.

Números aleatórios verdadeiros são difíceis de serem obtidos em grande

quantidade, razão pela qual se recorre aos números pseudoaleatórios gerados por

4

computadores (os computadores são sistemas determinísticos e, portanto, incapazes de gerar números aleatórios verdadeiros.). Como cada número gerado depende do anterior através de um algoritmo específico, a distribuição resultante pode estar sujeito à periodicidades, resultando numa distribuição de má qualidade. No entanto, por melhor que seja o algoritmo, após todos os possíveis números, dentro de uma determinada precisão, terem sido sorteados, a sequência irá se repetir.

.

Figura 2.3: Mapa da região onde se localiza principado de Mônaco, recortada.

Para exemplificar o tipo de aplicações do método de Monte Carlo, considere que se queira determinar a área ocupada pelo principado de Mônaco (figura 2.2). Uma técnica antiga consiste em recortar o mapa (figura 2.3) e determinar o peso relativo da área recortada (figura 2.4).

Figura 2.4:

Para ilustrar a aplicação do método de Monte Carlo, é feito o lançamento de 1000 pontos uniformemente distribuídos dos quais

110, marcados em vermelho, atingem a região do principado, resultando na estimativa de 11% da superfície ocupada pelo principado de Mônaco.

A relação de pesos da região recortada e da região total do mapa deve ser a mesma da relação entre as áreas.

5

Pelo método de Monte Carlo, pontos são lançados, aleatoriamente, sobre toda a região retangular, com a contagem dos pontos que caem sobre o principado de Mônaco (figura 2.4). A relação entre o número de pontos sobre o principado e o número total de pontos fornece a estimativa da superfície ocupada pelo principado. No exemplo foram lançados um total de 1000 pontos dos quais 110, marcados em vermelho, caíram sobre o principado, resultando na relação de áreas correspondente a 0,11, isto é, a área do principado corresponde a 11% da área total considerada. Quanto maior o número total de pontos lançados melhor será o resultado.

Em geral os cálculos baseados em Monte Carlo convergem lentamente com o aumento do número de pontos utilizados, sendo um método adequado para casos em que a precisão não seja um fator limitante.

2.1 Números e variáveis aleatórios

Quando se joga um dado, qualquer número pertencente ao conjunto de números inteiros de 1 a 6 pode ser sorteado com probabilidades iguais, em princípio. O resultado é um número aleatório. De maneira similar, quaisquer números sorteados usando roletas ou outros instrumentos similares cujo objetivo é escolher ao acaso um número dentre um conjunto de números pré-definido são números aleatórios, ou variáveis aleatórias se utilizados como argumentos de funções.

Como os processos mecânicos são lentos, nos computadores são usados geradores que, baseados em algoritmos matemáticos, simulam sorteios de números aleatórios, mais apropriadamente denominados números pseudoaleatórios. Os geradores de números aleatórios (a partir daqui não se fará mais distinção entre números pseudoaleatórios e aleatórios) baseados em computadores usualmente produzem

números uniformemente distribuídos dentro do intervalo �0, 1�. Para obter uma distribuição de probabilidades mais geral �(�) definida num

intervalo �, �� e com normalização

� �(�) � = 1��

,(2.1) pode-se usar a integral

� = � �(�) �(2.2)��

para R uma variável aleatória uniformemente distribuída no intervalo �0, 1� relacionada

com a variável aleatória X com distribuição �(�) no intervalo �, ��. Uma aplicação simples é para uma distribuição uniforme no intervalo �, ��,

�(�) = 1� − ,(2.3)

que resulta na transformação linear

�(�) = (� − )� + (2.4) correspondente a uma simples mudança de escala.

Outro caso simples é a distribuição exponencial

�(�) = ��� (2.5) definida na semi-reta 0 < � < ∞. A integral (2.2) resulta

6

�(�) = −!"(1 − �),(2.6) as novas variáveis X(R) distribuídas exponencialmente na semi-reta 0 < � < ∞.

Assim, nos dois exemplos acima, a distribuição uniforme das variáveis aleatórias

R no intervalo �0,1� podem ser convertidas nas distribuições desejadas. A figura (2.5) ilustra a distribuição exponencial na faixa abaixo da função exponencial.

Figura 2.5:

Gráfico da função de

distribuição exponencial e, abaixo, a distribuição obtida

com o lançamento de 3000 pontos.

Em geral não é possível obter a expressão analítica da integral (2.2), e a conversão

da variável aleatória uniformemente distribuída R para a variável X com distribuição �(�) não é uma questão trivial, devendo-se recorrer a procedimentos numéricos.

2.2 Técnica de rejeição de Neumann

A técnica de rejeição de Neumann permite obter variáveis aleatórias X com

distribuição p(x) no intervalo �, �� a partir das variáveis aleatórias R uniformemente

distribuídas no intervalo �0,1�. Baseia-se em testes repetitivos que podem ser resumidos a dois passos:

1 - Gere um primeiro número aleatório �$ uniformemente distribuído no intervalo �0,1� e converta-o para outro número aleatório �$ uniformemente distribuído no

intervalo �, ��. Se o sistema depender de mais de uma variável, o procedimento deve ser repetido para cada uma das variáveis.

2 - Gere um segundo número aleatório �% uniformemente distribuído no intervalo �0,1� e cheque a relação de desigualdade

�%&' < �(�$),(2.7) onde &' é o máximo absoluto da distribuição �(�). Se a relação for verdadeira, �$ será uma variável aleatória com a distribuição desejada. Se for falsa, rejeite o par (�$, �%) e retorne ao passo inicial. O procedimento deve ser repetido até obter um número estatisticamente significativo de variáveis aleatórias.

Na realidade, a condição (2.7) pode ser relaxada para

�%& < �(�$)(2.8)

7

para qualquer & > &', pois nem sempre é possível computar o valor exato do máximo absoluto da distribuição. A consequência é aumentar o número de pontos a serem testados e eliminados durante o processo de seleção, aumentando o tempo de computação. A figura 2.6 ilustra o procedimento de seleção de Neumann tomando como exemplo a distribuição radial �(+) = +%|�-'(+)|%(2.9) do nível ("!) = (30) do átomo de hidrogênio, cuja função radial é

�-'(+) = 2 / 13'0-% 11 − 2+3' +

2+%27'%2 ��3/(-�5).(2.10)

(a)

(b)

(c)

Figura 2.6: No quadro (a), o gráfico da distribuição. Em (b) uma amostra inicial de 3000 pontos uniformemente distribuída na região retangular limitada acima pela reta horizontal azul. Em (c) aparecem os pontos selecionados, 930 neste caso.

O objetivo da técnica de rejeição de Neumann é eliminar todos os pontos acima

da distribuição �(�) testando a condição (2.7) ou (2.8) para todos os pontos da distribuição inicial uniforme.

O conjunto dos pontos aceitos, mostrados na figura (2.6), quadro (c), tem a distribuição desejada, como mostra a projeção dos pontos selecionados sobre a superfície retangular, na figura (2.7).

Figura 2.7:

Distribuição dos

pontos selecionados coletados na área retangular.